发生吸引量不确定的离散交通网络设计模型

陆化普，蔚欣欣，卞长志

（1.清华大学交通研究所，北京100084；2.中国城市规划设计研究院,北京100044）

发生吸引量不确定的离散交通网络设计模型

陆化普1，蔚欣欣1，卞长志2

（1.清华大学交通研究所，北京100084；2.中国城市规划设计研究院,北京100044）

交通网络设计是交通规划的核心内容之一，而网络设计由依靠交通需求预测技术。为了改进传统的以确定性需求为基础的网络设计，文章以交通需求不确定性为基本前提，认为交通发生吸引量也是不确定的，并使用随机双层规划、均值方差和交通分配理论建立了发生吸引量不确定离散交通网络设计的基本模型。为了求解发生吸引量不确定的离散网络设计问题，开发了基于Monte Carlo模拟、遗传算法和交通分配算法的方法。Nguyen Dupuis网络的计算结果表明，需求不确定程度和政府决策者风险偏好等对规划方案具有重要影响。

离散交通网络设计；发生吸引量不确定；双层规划；遗传算法

0 引言

在交通网络设计问题中，往往是由政府部门在给定的约束条件下，确定规划方案，最优化交通系统性能，但是它不能控制出行者的选择行为；而出行者随着网络特性的改变调整决策，最小化出行费用。这是一个典型的领导者-追随者对策问题，通常采用下面的双层规划模型进行描述[1,2]。

其中y=y(x)是x的隐函数，由下面的问题决定：

上层模型（1）是规划者改善交通网络系统性能的最优决策问题。下层模型（2）是给定交通网络规划方案的出行者平衡问题。假设对于任意给定的上层决策变量x，都可以从下层问题求得唯一的平衡交通流量y=y(x)，称y(x)为反应或响应函数，反映网络用户的路径选择行为。交通网络设计模型就是在满足投资预算等约束条件下，考虑网络用户路径选择行为，寻找最佳网络设计决策方案x使系统目标函数F(x,y)最优。

但是以上的传统的固性需求交通网络设计，都没有考虑决策中存在的不确定性。交通需求不确定时，不同需求水平下的网络设计方案差异很大，决策者将面临较大的风险，为了降低交通网络设计方案对于不确定性的敏感性，需要利用不确定优化理论。

本文假定OD需求是服从一定概率分布的随机变量，进一步认为交通发生吸引量是不确定的，采用随机规划方法和交通分配方法描述交通发生吸引量不确定情况下的交通网络设计决策，进而构建随机双层规划模型，并给求解的方法。本文还将用算例表明这种考虑了发生吸引量不确定的交通规划模型是有实际应用前景的。

1 随机规划理论

经典数学规划理论与方法包括线性规划、非线性规划、多目标规划、动态规划等。然而，在管理科学、工程技术、军事决策等诸多领域都存在很多人为的或客观的不确定性因素，经典规划理论处理这类不确定的方法是灵敏度分析，即假定输入数据存在微小扰动，考察模型输出可能的变化。但是对于目标函数和约束条件相对复杂的问题，灵敏度分析方法很难取得前瞻性的结论。为了能够对不确定进行前摄处理，必须在建模阶段引入变量的不确定性，其中就包括本文使用的方法-随机规划（stochastic programming）方法。

当确定性问题中出现了随机变量ζ，则问题成为随机规划问题。在随机规划中，参数的不确定性使用概率分布函数来描述，其目标函数和约束条件需要根据概率意义理解[3,4]。基本的随机规划模型如下：

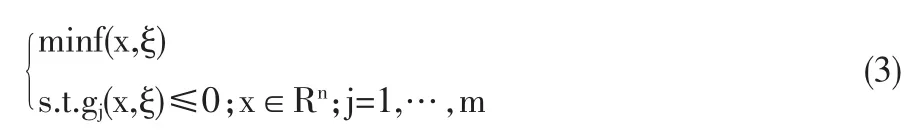
在期望约束下，使目标函数的期望值达到最优的数学规划，称为期望值模型。期望值模型是随机数学规划中最常见的形式之一，典型形式如下：

补偿随机规划（Stochastic Programming with Recourse）是一类典型的期望值模型，由运筹学大师Dantzig（1955）最先进行研究，该类模型的主要思路是在观察到随机变量实现之前便作决策，该决策可能产生对原约束条件的偏离，待随机变量实现之后，采取应急策略以对原约束条件的偏离今年新补偿[4]。带补偿的两阶段随机规划的典型形式如下：

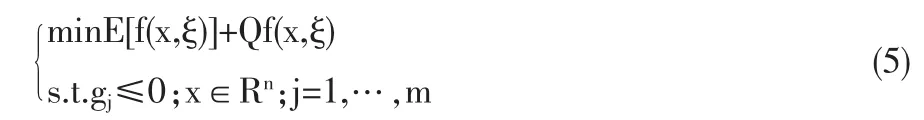
其中Q(x,ζ)是由于某些约束被违反而产生的一个额外补偿费用，定义如下：

其中q(y)是一个费用函数，Wj(y)是给定决策变量x和随机变量ζ的实现之后关于应急策略y的一个约束函数。本文采用这种方法为基础。

2 网络随机规划模型

基于随机规划理论的不确定交通网络设计模型，假定交通需求是服从已知概率分布的随机变量，以随机双层规划模型求解最优网络规划方案。Liu等（2007）建立需求不确定的连续交通网络设计双层模型，上层模型是期望总出行时间和投资成本的加权和，下层模型是不同需求情景实现下的UE模型，该文使用基于模拟的遗传算法进行了算例研究[5]。Sun和Turnquist（2007）建立了需求不确定的交通网络设计模型，该模型假定需求是分布已知的离散随机变量，对于需求的每个实现，交通流满足Probit随机用户均衡，上层目标是预算约束条件下极大化系统容量；考虑到双层规划求解的难度，设计了基于模拟退火的算法，并对美国集装箱港口网络进行了实例计算[6]。Ukkusui等（2007）研究需求不确定的连续交通网络设计问题。假定OD矩阵元素是概率分布已知的随机变量，以总出行时间期望值和标准差的加权平均作为优化目标。并以遗传算法进行求解，不同规模网络和预算水平的计算表明模型和算法的有效性。案例网络的计算结果还显示，鲁棒解与固定需求的网络设计解显著不同，忽略不确定性将过低估计网络范围的影响[7]。Partriksson（2008）以随机双层规划模型严格考虑需求的不确定性，其中上层规划极小化目标函数的期望值，下层是变分不等式表示的均衡条件。将鲁棒性定义为全局最优解相对于需求概率分布扰动的稳定性，并从数学理论上证明了特定随机双层规划模型具有鲁棒性[8]。

3 基于发生吸引量不确定的离散交通网络设计模型的建立

3.1 符号定义

N：交通网络的节点集合；

A：交通网络的路段集合；

Or：交通发生点r的发生交通量；

Ds：交通吸引点s的吸引交通量；

Prs：OD对rs之间的路径集合；

xa：路段a的交通流量；

ta(x)：路段a的行程时间阻抗函数；

ya：路段a对应的决策变量，ya∈{0,1}，其中ya=1表示路段采取新建或扩建策略，ya=0表示维持现状；

Ca：路段a的通行能力；

La：路段a的长度；

Ga(ya)：新建或扩建路段a的成本；

B：新建或扩建所有路段的预算；

Ω：不确定交通需求的所有可能情景集；

ω：不确定交通需求的任一实现；

pω：不确定交通需求情景ω的实现概率；

ρ：规划决策者对于网络出行时间均值和方差的权重；

ζ:交通分布/交通分配组合模型参数。

3.2 交通分布/交通分配组合模型

交通分布/分配组合模型的目的是克服传统四阶段预测模型存在的不一致。研究始于20世纪60～70年代，Tomlin（1971）首先进行了尝试[9]。Florian等（1975）和Evans（1976）提出了交通分布与交通分配的组合模型，其中交通分布使用指数阻抗函数的引力模型刻画，交通分配服从UE均衡，并应用凸规划理论完整地论述了等价于组合问题的最优化模型的存在性和解的唯一性[10,11]。针对FW算法求解组合模型存在的问题，Evans（1976）给出了二阶段求解算法（Evans算法）。Huang和Lam（1992）对该算法进行了进一步优化改进[12]。周溪召（2000）基于Logit模型建立了混合交通分布/交通分配组合模型[13]。Xu等（2008）对交通分布/交通分配组合模型提出了改进的基于起点的求解算法[14]。

本文采用的交通分布/交通分配组合模型可以用规划模型（7）表示。

其中（7）的第一式是目标函数，由交通分配目标函数和交通分布熵两项共同组成；第二式是路径流量与OD流量之间的守恒关系；第三式是发生交通量约束条件；第四式是吸引交通量约束条件。

3.3 双层规划模型建立

假定发生吸引交通量是满足给定分布的随机变量，其中情景ω对应的起点的发生交通量为，终点S的吸引交通量为，该情景的发生概率为pω。

发生吸引量不确定的离散交通网络设计模型由上层规划（8）和下层规划（8）共同组成，上下层规划通过网络决策变量y和路段交通量x相互联系。上层规划模型（8）是在资金预算约束下，政府决策者和规划人员选择新建和改建路段，最小化随机发生吸引需求在所有情景实现条件下的系统总出行时间均值和标准差。下层规划模型（9）是在上层规划模型确定的网络改进决策条件下，每种发生吸引量情景对应的交通分布/交通分配组合模型。

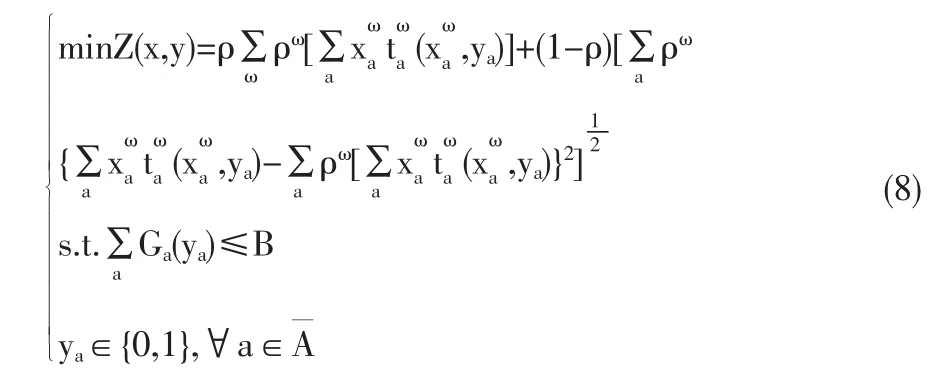
其中x=x(y)是y的隐函数，由下层规划问题（9）决定：

路段a的出行时间使用BPR函数描述。

均值和标准差之间的权衡使用权重系数ρ表示，ρ∈[0,1]，反应政府决策者和规划人员对不确定性的平均性能和偏离平均性能离散程度的偏好；ρ取值越大，规划决策者对不确定性导致的风险厌恶越强。

4 模型求解算法

4.1 算法流程

采用基于模拟的遗传算法[15]求解发生吸引量不确定的离散交通网络设计模型，算法流程如图1，具体步骤如下：

(1)初始化

①定义GA参数，主要包括：染色体编码方案，种群规模，种群进化最大代数，代沟，交叉概率，变异概率。

②确定发生吸引量抽样规模，生成初始种群。在初始种群个体生成时，执行预算约束判断，直到获得足够数量的初始可行解。

(2)对每一代种群中的每个个体进行处理

①根据染色体编码方案，更新交通网络结构和参数；

②发生吸引交通量随机抽样，对每个发生吸引交通量实现进行交通分布/交通分配组合模型计算；

③根据所有发生吸引量情景下的路段流量和时间，计算上层目标函数。

(3)使用GA更新种群

①根据上层目标函数计算个体适应度；

②根据适应度进行个体选择；

③执行交叉和变异操作；

④对产生的中间种群个体执行预算约束判断；

⑤形成新一代种群。

(4)生成最优解

在第（2）步执行发生吸引交通量的随机模拟过程时，为了保证区域发生和吸引交通量的平衡，需用利用发生交通量对吸引交通量进行平衡。即执行如下步骤：

4.2 下层模型求解算法

本文使用凸组合法求解下层模型。设在第n步迭代上，OD流量为，路径流量为，通过求解下面的线性规划问题，我们可以得到目标函数在处的下降方向。

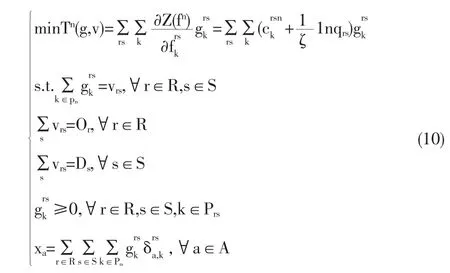
将（10）中的第3、第4式代入第1式中，可以重写问题（10）为

问题式（11）是运筹学中有名的Hitchcock运输问题，有成熟的计算方法。决定了后，将其安排到最短路径上得到路段流量是下降方向。

下面给出整个算法的具体步骤：

(4)确定步长。

(5)更新流量。

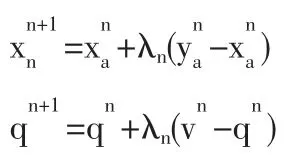
解；否则令n=n+1，返回第（1）步。

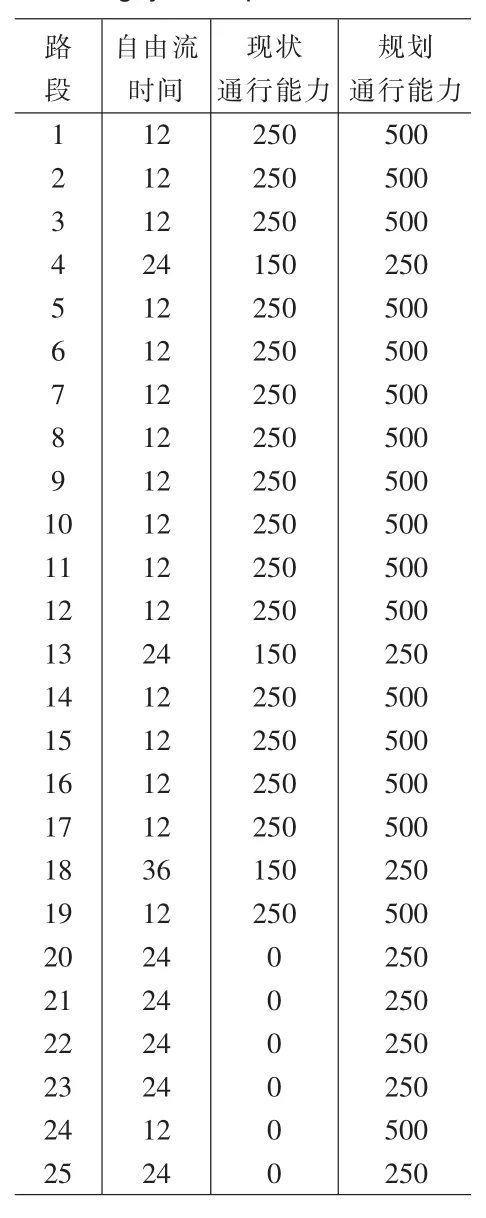
表1 Nguyen Dupuis网络基本属性

5 案例研究

5.1 网络结构

本论文研究采用Nguyen和Dupuis（1984）的测试网络作为案例，该网络拥有13个节点，19条路段，4个OD对。网络基本结构如图2，其中红色节点表示交通需求发生点，蓝色节点表示交通需求吸引点，实线表示现状路段，虚线表示待新建路段，表1是网络的基本属性信息，包括自由流时间、路段现状通行能力、规划通行能力、建设成本等。表2是OD需求信息，包括确定性需求和截尾正态分布交通需求两种情况。

表2 OD交通需求基本情况

表3 情景基本参数

表4 计算结果

5.2 计算结果

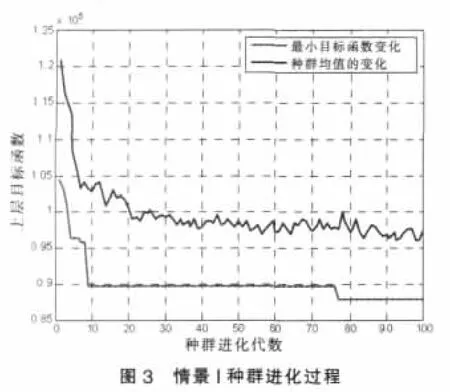
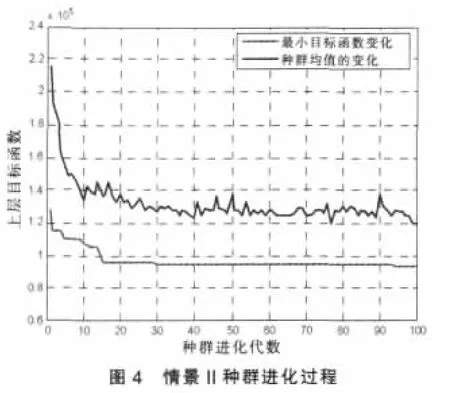
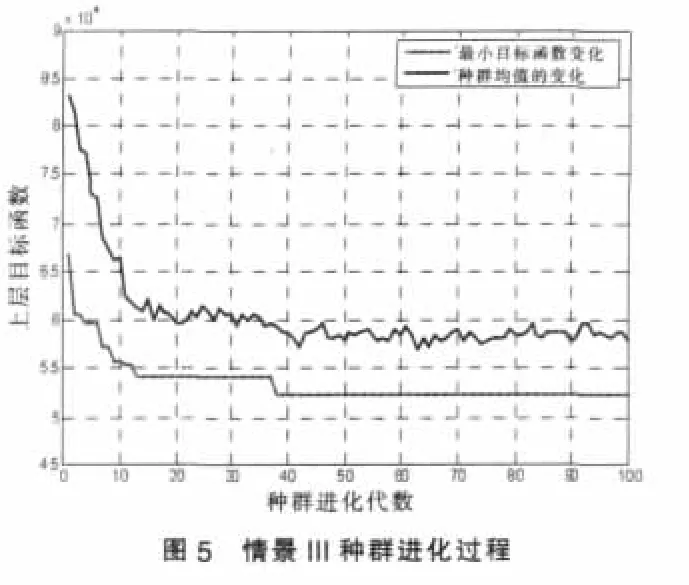
假定发生吸引量服从截尾正态分布，情景分析发生吸引则{yn-xn,vn-qn}就量不确定程度和决策者风险偏好对网络规划方案的影响，其中情景V为并不考虑交通分配与分布的情景。遗传算法基本参数为：种群规模40，进化代数100，染色体长度为25，代沟0.9，交叉概率0.8，变异概率0.01。

图3～图6是遗传算法求解的种群进化过程，表4是计算结果，可以得到如下结论：

（1）其它参数相同时，发生吸引量不确定程度不同，交通网络规划设计方案不同。

（2）比较情景I和情景V的计算结果可以发现，在发生吸引总量相同的条件下，下层模型（如交通分布/分配组合模型或是用户均衡模型）的不同将导致网络设计方案不同。

（3）情景II～IV的对比可以看到，发生吸引量随机程度相同，网络规划方案由上层决策者的风险偏好决定。

6 结论

本文假定发生交通量和吸引交通量是概率分布给定的随机变量，以交通分布/交通分配组合模型描述出行者的终点选择和路径选择行为，并将其作为下层规划嵌入发生吸引交通量不确定的离散交通网络设计模型。而利用Monte Carlo模拟和遗传算法则有效解决了随机双层规划的求解。Nguyen-Dupuis网络的计算结果表明，需求不确定程度和政府决策者风险偏好等对规划方案具有重要影响。

[1]腾春贤,李智慧.二层规划的理论与应用[M].北京:科学出版社,2002.

[2]高自友,宋一凡,四兵锋.城市交通连续平衡网络设计理论与方法[M].北京:中国铁道出版社,2000.

[3]Birge J R,Louveaux F.Introduction to Stochastic Programming[M].New York:Springer,1997.

[4]Danztig G.Linear Programming underUncertainty[J].Management Science,1995,1(3).

[5]Liu Haixu,Hu Ji,Pu Yun.Continuous Network Design Problem Considering Stochastic demand[J].In 1st International Conference on Transportation Engineering,Chengdu,2007.

[6]SunYao,TurnquistMA.Investmentin Transportation Network Capacity under Uncertainty:simulated Annealing Approach[J].Transportation Research Record,2007,2039.

[7]Ukkusui S V,Mathew T V,Waller S T.Robust Transportation Network Design under Demand Uncertainty[J].Computer-Aided Civil and Infrastructure Engineering,2007,22.

[8]Partriksson M.Robust Bi-Level Optimization Models in Transportation Science[J].Philosophical Transactions of the Royal Society A,2008,366.

[9]Tomlin J A.A Mathematical Programming Model for the Combined Distribution-assignment of traffic[J].Transportation Science,1971,5(2).

[10]Florian M,Nguyen S,Ferland J.On the Combined Distribution assignment of traffic[J].Transportation Science,1975,9(1).

[11]Evans,S P.Derivation and Analysis of Some Models for Combining Trip Distribution and Assignment[J].Transportation research, 1976,10(1).

[12]Huang H J,Lam W H K.Modified Evans’Algorithms for Solving the Combined Trip Distribution and Assignment Problem[J]. Transportation Research B,1992,26(4).

[13]周溪召.混合交通运量分布与均衡配流组合模型研究[J].系统工程学报，2000,15(2).

[14]Xu Meng,Anthony Chen,Gao Ziyou.An Improved Origin-Based Algorithm for Solving the Combined Distribution and Assignment Problem[J].European Journal of Operational Research, 2008,188.

[15]Holland J H.Adapation in Natural and Artificial Systems[J].Ann Arbor:The University of Michgan Press,1975.

（责任编辑/亦民）

U491.1

A

1002－6487（2011）06－0008-05

教育部博士点基金资助项目（20070003065）；国家高技术研究发展计划资助项目（863计划）（2007AA11Z202；2007AA11Z233）

陆化普(1957-)，男，辽宁铁岭人，教授，博士生导师，研究方向：交通需求预测、交通管理、交通控制理论与方法。