金融风险管理M-V方法的资产组合灵敏度分析

吴勋，徐永春

（1．西安石油大学经济管理学院，西安710065；2．北京天相投资顾问有限公司，北京100140）

金融风险管理M-V方法的资产组合灵敏度分析

吴勋1，徐永春2

（1．西安石油大学经济管理学院，西安710065；2．北京天相投资顾问有限公司，北京100140）

文章基于均值－方差（M-V）风险计量技术，分析了资产组合在资产品种减少的敏感性，通过引入协方差扰动，建立相关的M-V组合模型。同时和原模型进行比较，分析有效前沿的变化，探究其经济意义。

M-V；投资组合；有效前沿

0 引言

投资者在构建投资组合时，不同的投资者有着不同的期望，通常理性投资者会选择在持有期内风险最小的投资组合。但是由于收益与风险的随机性，投资偏好的时变性，投资者需要经常调整所选择资产的类别和数目，那么就面临这样一个问题：淘汰什么样的资产，吸收那些资产，才能使投资收益达到最理想的状态，因此研究关于资产数量变化情况下M-V资产组合有效前沿特征的灵敏度问题，将有着重要的理论和现实意义。因此本文就市场不存在无风险收益资产且允许卖空的条件下，研究资产数减少的情况下M-V投资组合有效前沿的漂移问题，探究其经济意义。

1 M-V投资组合模型

假设t0时刻市场上n种资产，且组成的投资组合为x=为投资组合集

n)}。收益率为ri(i=1,2,…，n)，收益率的协方差Vn是正定对称矩阵分别表示投资组合的期望收益率和方差。并假设：(1）不存在无风险收益资产，且允许卖空；

(2）n种资产具有线性不相关的收益特征，即任一资产的收益均不能表示为其余n-1个资产收益的线性组合；

(3）每种资产的期望收益率不完全相等。

t0时刻最优资产组合选择问题可由下面模型来描述：

这里In表示n个分量均为1的n维列向量，Rn=(E(r1),E (r2),…，E(n))T是资产收益率的均值向量。由文献[1]可得最小方差投资权重为：

式中

在(σ,μ)坐标系下该方程表示一条双曲线，最小方差资产组合为该双曲线的右支，而有效前沿为其右支的上半部分。全局最小方差资产组合为双曲线右支的顶点，其期望收益率与风险分别为：

2 M-V投资组合前沿对资产数量减少的敏感性

假定t时刻资产种类减少到n-1种，假设淘汰了第n种资产，剩下的n-1种资产相关性结构必然会产生影响，现考虑由于减少一种资产后投资组合前沿曲线的变化的特征。

假设淘汰的第n种资产对协方差矩阵Vn-1中的元素σij影响程度为εij，εij为扰动因子，受到扰动后的协方差Vn-1可表示成正定矩阵，记δT=(σn1,σn2,…，σn,n-1)，于是：

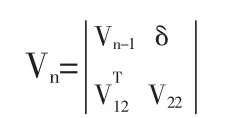
又有分块矩阵求逆可得：

假设减少资产后，每种资产的期望收益率不完全相等，由文献[2]得个风险资产所组成的新的投资组合集的有效前沿方程为：

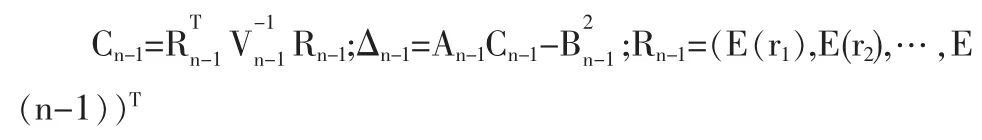
并且，由候为波（2000）等的结果，有效前沿曲线方程的系数有下面的递推关系式成立：

下面将f≠0与f=0两种情形分别讨论。这里f描述了所淘汰的资产与余下资产的协方差向量和协方差矩阵之间的关系。

由（3）、（5）和（6）可得

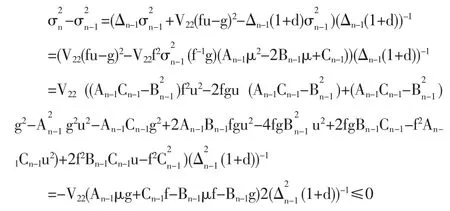
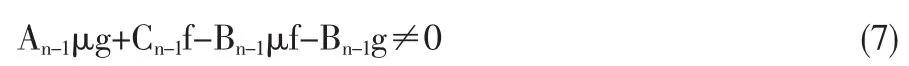
成立时，方差是严格增加的，即有效前沿将随着资产数的减少向右移动。

成立时，渐近线的斜率是严格减少的，即双曲线张口变小，投资有效前沿向下移动，投资范围变小，从而投资效益将有所损失。

当f=0时，有An=An-1，Bn=Bn-1，△n=△n-1+V22An-1g2。此时全局最小方差资产组合的收益和方差均不改变。

若g=0，有Cn=Cn-1，△n=△n-1，这时第n种资产的减少对资产组合的有效前沿不产生影响（这样的资产称为相对无效资产，否则称为有效资产，它是相对某一资产而言的，此处是相对前n-1种资产而言的）。

若g≠0时，由△n=△n-1+V22An-1g2可得：

条件（7）和（8）是判别有效前沿移动方向的依据，并有下面定理。

定理1 如果f2+g2≠0，则条件（2.3）与（2.4）中至少有一个成立。

证明：用反证法，令（2.3）与（2.4）均不成立。由f2+g2≠0知f和g中至少一个不为零，设f≠0，则由（2.4）不成立得fBn-1-gAn-1=0，Bn-1gAn-1/f由（2.3）不成立得An-1μg+Cn-1f-Bn-1μf-Bn-1g=0，将Bn-1=gAn-1/f代入上式得Cn-1f-An-1f-1g2=0，进而有Cn-1= An-1f-2g2，由此可得同△n-1>0矛盾。从这个定理可知，若则与△n/An≥△n-1/An-1至少有一个严格不等式，其经济意义是：当f和g中至少一个不为零时，资产数量的减少对有效边缘产生影响，或向右下移动，或双曲线开口变小。

3 灵敏度分析在金融风险管理中的意义

本文基于M-V模型，在考虑协方差矩阵受到扰动情形下，研究了资产组合有效前沿的问题。在市场不存在无风险收益资产且允许卖空的条件下，得出了当f2+g2≠0时，资产数量的减少对有效边缘产生实质影响，或向右下移动，或双曲线开口变小的结论。这些分析有助于投资者更好的调整其投资资产集合，淘汰一些业绩较差的资产，吸收一些较好的资产（所谓较差的资产就是那些存在与否对有效前沿几乎不产生影响的资产），达到规避风险，取得更多收益的目的。

囿于篇幅，仅考虑了投资组合前沿曲线对资产数量减少的灵敏度分析，对资产数量增加的情形将另文阐述。但研究还有一些值得继续进行的地方，一是考虑资产数目增加或减少时有效前沿问题，二是可以在组合中加入无风险资产。

[1]XueHonggang．Portfolio'sSensitivityAnalysiswithoutRiskless Asset[J]．Journal of Engineering Mathematics，2003，(6)．

[2]Jarrow R A，Maksimovic V，Ziemba W T．Finance[M]．Handbook in Operations Research and Management Science，North-Holland Elsevier，1995．

[3]高全胜，李选举．基于的投资组合对资产变化的敏感性分析[J]．数量经济技术经济研究，2005，(6)．

[4]徐成贤．金融工程计算[M]．北京：科学出版社，2007．

[5]袁先智．金融风险管理的新挑战及次贷危机的启示[J]．管理评论，2009，（3）．

[6]史树中．金融学中的数学[M]．北京：高等教育出版社，2006．

(责任编辑/亦民)

0211

A

1002－6487（2011）06－0081-02

全国教育科学“十一五”规划项目（DFA060116）

吴勋（1978-），男，河南南阳人，博士，研究方向：风险控制方法。

徐永春（1978-），男，安徽蚌埠人，博士，研究方向：金融资产投资组合分析。