新型麻花钻圆锥面后刀面刃磨参数的近似求解*
2011-10-18汤爱民
曾 滔 汤爱民
(株洲钻石切削刀具股份有限公司,湖南株洲412007)
麻花钻是机械加工行业中普遍使用的一种孔加工刀具。提高麻花钻的切削性能可以大大提高孔加工的质量和效率,降低加工成本。在不改变麻花钻基体材料的条件下,其切削加工性能的优劣主要依赖于钻尖结构。麻花钻钻尖结构包括非共轴螺旋面[1]、双平面、圆锥面、螺旋面、圆柱面、椭球面、双曲面和群钻钻尖[2]等多种。为了设计出切削性能更好的钻头,学者在钻尖的数学模型及其刃磨方法方面进行了大量的研究[3-6],其中很多成果与传统直线刃圆锥面钻尖的刃磨有关。随着刀具技术的快速发展,一种新型结构的硬质合金麻花钻在通用加工领域表现出了卓越的切削性能。与传统圆锥面钻头不同的是:这种圆锥面钻头芯厚较大,顶角为140°,主切削刃呈内凹曲线,如图1所示。为了建立该钻头精确的三维实体模型,从而对其结构和刃磨工艺进行优化,有必要对该钻尖尤其是后刀面的数学模型和刃磨参数的求解进行研究。由于推导精确求解新型圆锥面麻花钻后刀面刃磨参数方程组的过程相当复杂,而且其变量多,理论性强,难以解决工程实际问题,因此,采用近似的求解方法更适用于工程上的需要。

1 圆锥面后刀面的数学模型
如图2所示,以钻尖横刃中点为原点建立钻头结构坐标系O-XYZ,X轴平行于钻头外缘转点与内刃转点连线在端平面的投影,Z轴由钻柄指向钻尖。麻花钻圆锥面后刀面由一条与锥轴夹角为θ的母线绕锥轴旋转而成,该圆锥面母线和锥轴构成的平面与钻头结构基面XOZ平行,并且距离为S。以圆锥面锥顶为原点建立锥面坐标系O*-X*Y*Z*,Z*轴与锥轴重合,正向指向锥顶,与Z轴夹角为σ;Y*轴与Y轴平行且方向相同;两坐标系原点在Z*轴上的投影长度为H。

在锥面坐标系O*-X*Y*Z*中,圆锥面的方程如下:

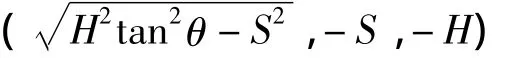

将式(2)代入到式(1)中可以得到结构坐标系中的圆锥面后刀面方程为

另一个与之关于Z轴对称的后刀面方程为

2 圆锥面后刀面刃磨参数的求解
设麻花钻的外缘转点到钻头结构基面XOZ面的距离为rc,半顶角为φ,结构圆周后角为αf,横刃斜角为ψ。
2.1 刃磨参数与横刃斜角的关系
麻花钻横刃斜角ψ是横刃即两后刀面交线在端平面的投影曲线在原点处的切线与X轴的夹角,联立式(3)和(4)得到横刃方程,据此可求得横刃曲线在原点处的切向量为
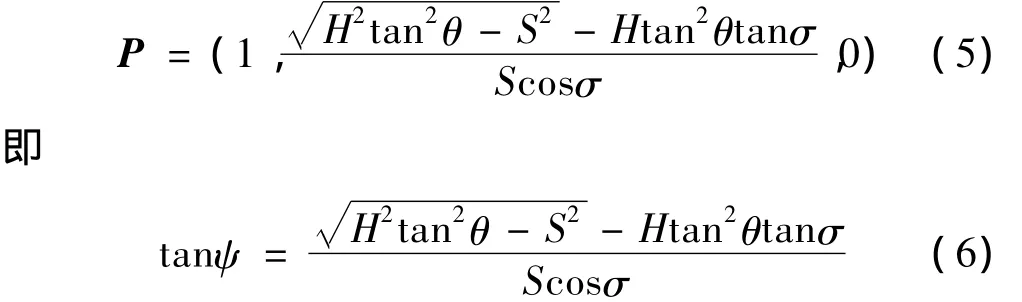
2.2 刃磨参数与结构圆周后角的关系
麻花钻轴向结构后角αc是在平行于钻轴且垂直于钻头结构基面的平面内测量的钻尖外缘转点处后刀面与端平面之间的夹角;而结构圆周后角αf是在平行于钻轴且垂直于钻头半径的圆柱面内测量的钻尖外缘转点处后刀面与端平面之间的夹角。设钻头外缘转点处的钻心角为 μ(sinμ=rc/R),则 αc与 αf之间有如下关系[2]:
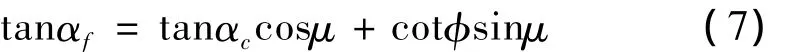
圆锥面后刀面与平面X=Rcosμ的交线方程为

钻尖外缘转点的坐标为(Rcosμ,Rsinμ,-Rcosμ/tanφ),方程(8)两边对Y求微分得,
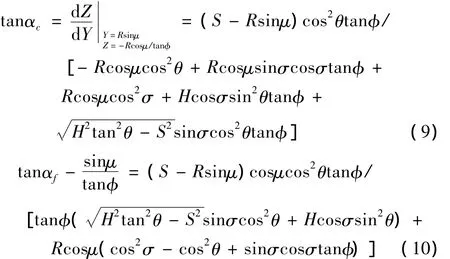
2.3 刃磨参数与半顶角之间的关系
麻花钻半顶角φ是其主切削刃在结构基面的投影曲线在外缘转点处的切线与钻轴的夹角。新型圆锥面麻花钻的主刃虽为内凹曲线,但主刃在结构基面的投影曲线近似为直线,用投影曲线上外缘转点与内刃转点连线近似替代外缘转点的切线。令式(3)中Y=rc,则有,

方程(11)两边对Z求微分得,

结合式(6),式(12)可进一步化简为

2.4 求解刃磨参数的方程组
联立式(6)、(10)、(13)得到求解后刀面刃磨参数σ、θ、H和S的方程组为
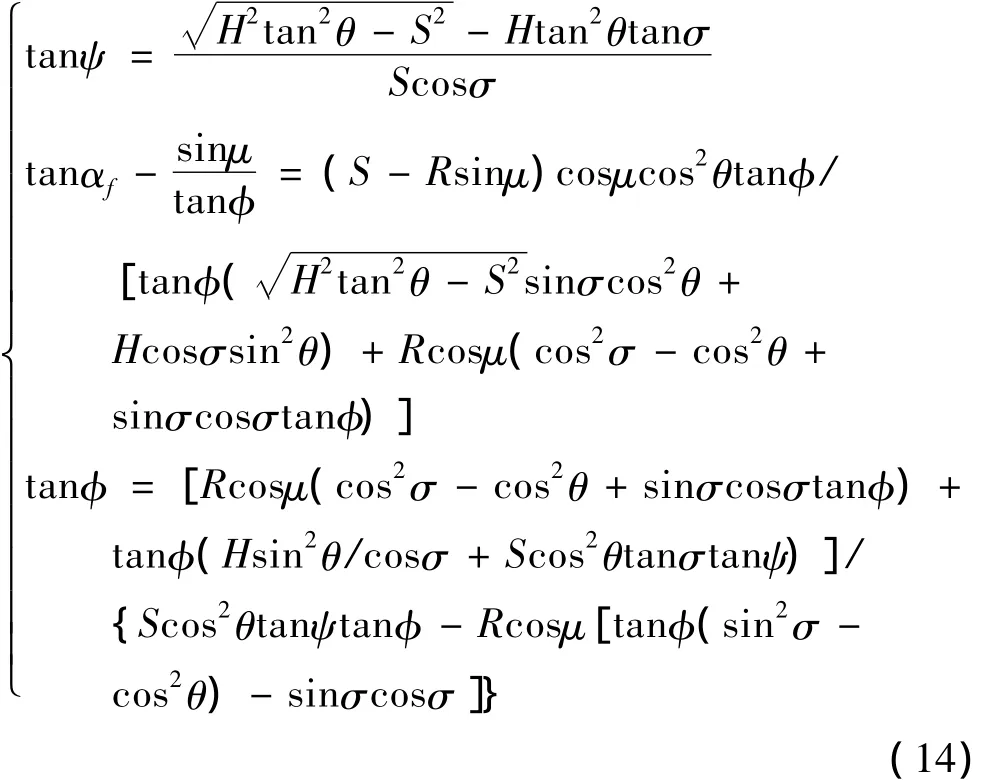
显然3个方程不能确定4个未知数的唯一解,在实际应用中,可根据麻花钻的设计要求确定合适的σ值,再利用数学工具Matlab就可求解出上述方程组θ、S和H的数值。
3 刃磨参数求解方程组的验证
新型圆锥面麻花钻半径为R,后刀面相关参数设计值为:rc=0.15R,φ =70°±2°,ψ =55°±5°,αf=7°±1°。固定 σ 值在区域[10°,45°]内[2],以 5°为间距确定8组σ,分别求出每组σ对应的刃磨参数θ、S、H的值,再根据刃磨参数建立对应的麻花钻三维模型(见图3),并对φ、ψ和αf的值进行检测,结果见表1。从结果来看,虽然刃磨参数的求解采用的是近似的解法,但“加工”出来的产品,其设计参数的测量值与理论值几乎完全吻合,这证明了新型圆锥面麻花钻后刀面刃磨参数的近似解法完全能满足工程需要。

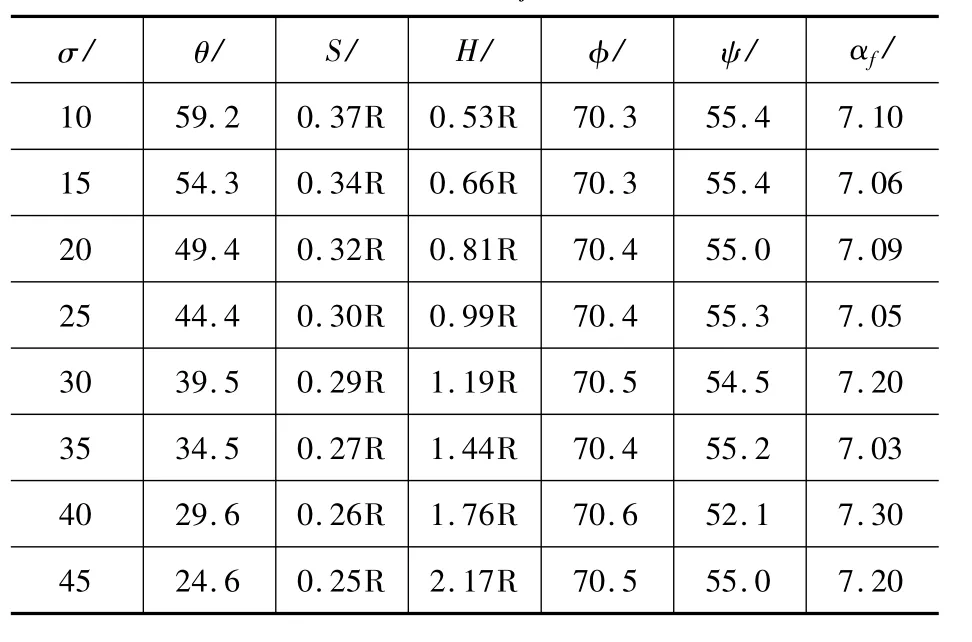
表1 σ与 φ、ψ、αf的变化关系 (°)
4 结语
根据麻花钻半顶角的定义,半顶角与钻头主切削刃的空间曲线形状有很大关系。求解圆锥面后刀面的刃磨参数必须推导出主切削刃空间曲线的方程,这对于刃形复杂的新型圆锥面麻花钻来说,是一项十分繁杂的工作。本文提出的圆锥面后刀面刃磨参数的近似解法,完全避开了这一难题,而且事实也证明,这种近似解法能够很好地满足工程需要。当然,该近似解法也适用于一般直线刃圆锥面麻花钻。
[1]周志雄,罗霞玉,杨军,等.非共轴螺旋面钻尖角度的求解[J].湖南大学学报,2001,28(3):32-36.
[2]倪志福,陈璧光.群钻—倪志福钻头[M].上海:科学技术出版社,1999.
[3]吕彦明.锥面刃磨可展直纹面与后刀面刃磨[J].工具技术,2003,37(11):40-43.
[4]向文江,周志雄.新型螺旋面微钻头数控刃磨技术的研究[J].现代制造工程,2006(5):7-9.
[5]熊良山,师汉民,陈永浩.曲线刃钻头柱面后刀面的刃磨[J].中国机械工程,2007,18(10):1165-1192.
[6]曾滔,周志雄,汤爱民.基于某工具磨床的群钻数学模型及其仿真研究[J].制造技术与机床,2008(10):68-71.
