主成分分析法在辽宁地区地震预测中的应用①
2011-10-16李永振
李永振
(辽宁省地震局,辽宁沈阳 110034)
主成分分析法在辽宁地区地震预测中的应用①
李永振
(辽宁省地震局,辽宁沈阳 110034)
采用多因子分析的主成分分析法,选择与地震活动强度有关的地震频次N(ML≥3.0)、b值、η值、Mf值、A(b)值和Ac值等6个参量进行分析,实现对上述参量的有效约简,得到反映地震强度特征的综合指标W。发现指标W在辽宁海城7.3级、岫岩5.4级地震前出现明显的异常变化,震后恢复。表明综合指标W可以较好的反映地震活动的异常特征。
辽宁;地震活动强度参数;主成分分析法;相关性;贡献率
Abstract:Using the primary components analysis method,six main parameters for indicating seismicity strenth such as frequency N(ML≥3.0),b value,ηvalue,A(b)value,Mfvalue,Ac-value are selected to analyse.The parameters are simplified effectively and a new synthetic index Wfor indicating seismicity strenth is obtained.It is found that the index Wappeared obvious anomalies before Haicheng MS7.3earthquake in 1975and Xiuyan MS5.4earthquake in Liaoning province,and returned after events.It is shown that the synthetic index Wcan reflect anomalous characterisitic of seiemicity well.
Key words:Liaoning province;Seismicity strenth parameter;Primary components analysis method;Relativity;Contribution rate
0 引言
当今世界各类数据量正在以指数增长。数据挖掘[1]就是在数据库中对数据进行一定的处理,从大量不完全的、有噪声的、模糊的、随机的数据中提取隐含的、事先未知的、但又是潜在有用的信息和知识的过程。在数据挖掘中数据清洗是一个重要环节,包括去噪声,填补丢失的域,删除无效数据,对时序数据的整理和归并,以及数据属性的约简等。王炜等[2]就用主成分分析法对地震活动性参数进行了约简,同时用该方法在江苏溧阳6.0级地震中进行了应用[3]。
主成分分析方法是将描述样本特征的多个可能有一定相关性的指标化为少数几个综合指标的一种统计分析方法,能够在最大限度地保留原有信息的基础上对高维变量系统进行最佳地综合与简化,并能够客观地确定各个指标的权数,避免了主观随意性。应用主成分分析法可以找出由若干个指标线性组合而成的综合指标,即若干个主成分,同时彼此之间相互独立。
目前在地震活动分析中存在许多预报指标,这类参数数量较多,同时它们之间还可能存在一定的相关性[4-5]。另外在实际预报中常常出现有些参数在一些中强以上地震前出现较明显的异常,而另一些参数并不出现异常。这些都给实际预报带来困难。为解决预报参数过多而造成预报意见的不一致。本文选用1970年以来辽宁地区2次5级以上地震前后震中附近地区的地震资料,选择与地震活动强度有关的6个参量,即3级以上地震的频次N、b值、η值、A(b)值、Mf值和Ac值进行主成分分析,以期得到一个反映地震强度异常的综合指标。
1 主成分分析法
主成分分析法旨在力保原始数据信息丢失最小的情况下,对高维变量空间进行降维处理,经过线性变换和舍弃部分信息,以少数的综合变量取代原有的多维变量。
设原始变量为x1,x2,…,xp,进行主成分分析后得到的主成分(综合变量)为z1,z2,…,zm(m<p),它们是x1,x2,…,xp的线性组合(m<p)。新变量z1,z2,…,zm构成的坐标系是在原坐标系经平移和正交旋转后得到的,称其空间为m维主超平面。在主超平面上第一主成分z1对应于数据变异(贡献率e1)最大的方向,对于z1,z2,…,zm,依次有e2≥,…,≥em。因此,z1是携带原始数据信息最多的一维变量,而m维主超平面是保留原始数据信息最大的m维子空间。
主成分分析法的步骤如下:
(1)为了排除数量级和量纲不同带来的影响,首先对原始数据进行标准化处理:
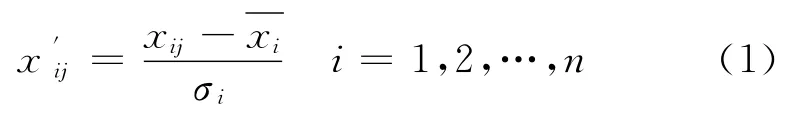
式中,xij为第i个指标第j个样本的原始数据;xi和σi分别为第i个指标的样本均值和标准差。
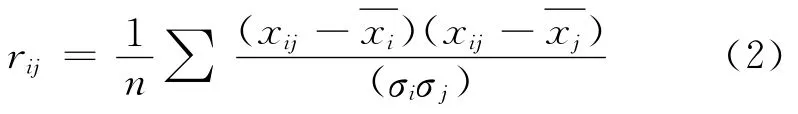
(3)根据特征方程│R-λI│=0,计算R的特征根λi,并使其从大到小排列:λ1≥λ2≥…≥λp,同时可得对应的特征向量u1,u2,…,up,它们标准正交。u1,u2,…,up称为主轴。这里I为单位矩阵。
(4)计算贡献率
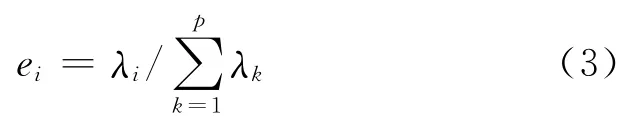
和累计贡献率
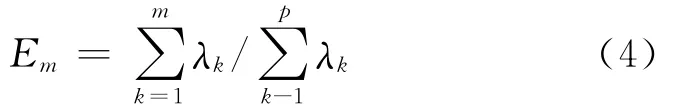
(5)计算主成分
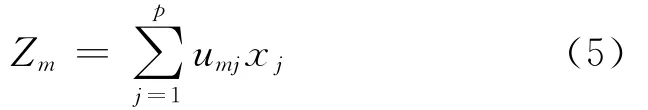
(6)一个m维主超平面究竟以多大的精度来近似代替原始变量系统才能确保尽可能多的原始数据信息?这可以通过求累计贡献率Em来判断。一般Em>85%的最小m(m<p),则可得主超平面的维数m,从而可对m个主成分进行综合分析。
(7)根据主成分分析得到的主成分Zi和相应的权值(贡献率)ei,计算本文定义的反映地震活动时、空、强异常特征的综合指标

由于m个主成分已基本保留了这些预报参数的信息,所以综合指标W包含了这些参数从不同侧面反映地震活动时、空、强异常的基本特征。本文选择了从不同侧面反映地震活动时、空、强特征的一些参量:地震频次N(ML≥3.0)、b值、η值、Mf值、A(b)值、Ac值6个参量进行主成分分析。
2 地震实例
2.1 1975年海城7.3级地震
1975年2月4日辽宁海城发生MS7.3地震。图1为地震发生前后震中周围300km范围内的一些地震活动性参数随时间变化曲线。除地震频次N(ML≥3.0)外,其它参数计算所选取的起始震级为ML2.0。参数计算累计时间为1年,滑动步长为1个月。从图1可以看到,7.3级地震前这些参数各有所异,大多参数在这次地震前的异常变化并不显著。
表1为通过主成分分析方法得到的上述参量在各主成分中的系数(特征向量)、特征值与贡献率。当取3个主成分时累计贡献率已达到93%;当取4个主成分时累计贡献率已达到98%。这表明取前3个主成分已包含了样本中的绝大部分信息量。由表1可知,主成分1中的A(b)、Mf值系数较大,是构成主成分1的主要参数;主成分2中的地震频次b值、η值系数较大,是构成主成分2的主要参数;主成分3中的Ac值、N值(ML≥3.0)系数较大,是构成主成分3的主要参数。
本文取前3个主成分根据式(5)计算地震综合指标W。图2反映了海城7.3级地震前后震中附近地区地震活动时、空、强异常特征的综合指标W随时间的变化。可以看到,在1975年海城7.3级地震前0.5年左右时间海城震中附近地区W值出现明显抬升的形态,异常幅度近1.0,震后异常逐渐恢复到正常范围内波动。
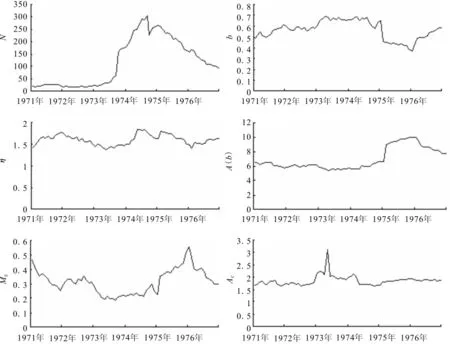
图1 海震地震前各地震参数曲线Fig.1 Curves of different seismic activity parameters before Haicheng MS7.3earthquake in 1975.
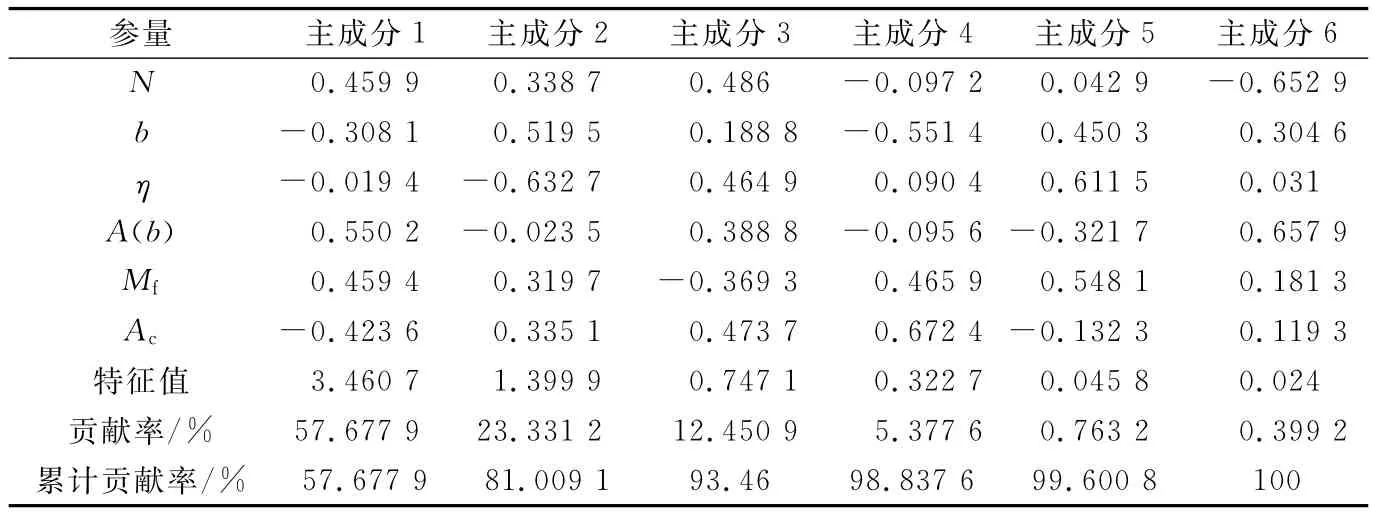
表1 各参量在各主成分中的系数(特征向量)、特征与贡献率
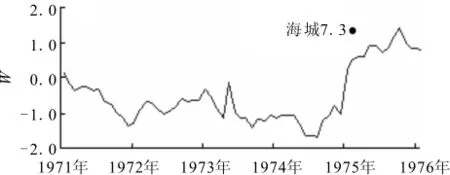
图2 海城地震前后地震强度综合指标W值的变化Fig.2 Curve of earthquake intensity synthetic index W before and after Haicheng earthquake.
2.2 岫岩5.4级地震
本文选取1970年以来东北地区(38°~55°N,117°~135°E)小震目录,考虑到地震孕育过程中的可能影响范围及东北地区地震活动实际情况,对岫岩5.4级地震选取200km左右圆域。除地震频次N(ML≥3.0)外,其它参数的计算选取ML2.0地震,并剔除余震,资料计算时间窗为12月,滑动步长为1个月。
采用与海城7.3级地震震例相同的主成分分析方法,取累计贡献率Em>85%的最小m(m<p)确定主成分个数m。在此基础上对m个主成分使用式(5)进行综合分析,得到反映地震活动时、空、强异常特征的综合指标W,并计算其在中强以上地震前后随时间变化曲线(图3)。由图3可知,W值大体在0以下波动,在中强震发生前1年左右的中期阶段出现明显的增高异常,异常高值通常超过1.0,这与文献[6]研究一致。
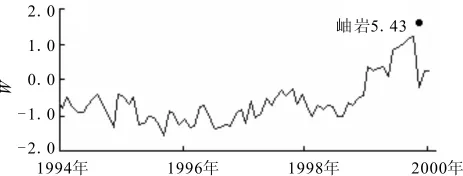
图3 岫岩地震前W值异常Fig.3 The Wvalue anomaly before Xuyan earthquake.
以上两个震例初步表明,反映地震时、空、强异常特征的综合指标W在震中附近地区震前的异常变化明显,可以较好地反映地震活动异常。
3 主成分对综合指标W值的影响
图4为对与地震活动强度有关的6个参量进行主成分分析时得到的3个公共因子得分随时间变化曲线。可以看到图4中综合指标W值的基本形态主要由主成分1确定,这是由于主成分1的方差贡献率最大,达到58%。主成分1主要反映了异常相对较好的Mf值、A(b)值2个参数的信息。其它2个成分得分各有所异,且异常变化特征不甚显著,但因为它们的贡献率较小,因此综合指标W值可以较好地反映出震前的异常变化。由此可以看出,因子分析可以通过研究各参量的相关矩阵内部结构,得到各参量的因子载荷和因子贡献率,将一些包含异常信息较大的参量和因子赋予较大的权值,从而使得综合指标W值的异常变化明显。
4 结论
目前在地震预测中由于地震活动性参数较多,指标之间有一定的相关性,因而所得的统计数据反映的信息在一定程度上有重叠;而且无论在正常情况还是异常情况下各个参数的形态变化各不相同[7-8]。这不但给分析预测工作带来不必要的麻烦,还可能存在主观片面性,不能很好地抓住事物的主要矛盾。而主成分分析有可能改善这一问题。主成分分析法可在力保原始数据信息丢失最少情况下,对高维变量空间进行降维处理,经过线性变换和舍弃部分信息,以少数的综合变量取代原有的多维变量。本文用主成分分析得到综合反映地震活动综合特征的W值,包含了以前描述地震活动强度各参数的绝大部分信息,在辽宁2次中强地震前出现明显的异常变化,表明综合指标W可以较好地反映地震活动异常特征,在地震预报中具有良好的应用前景。
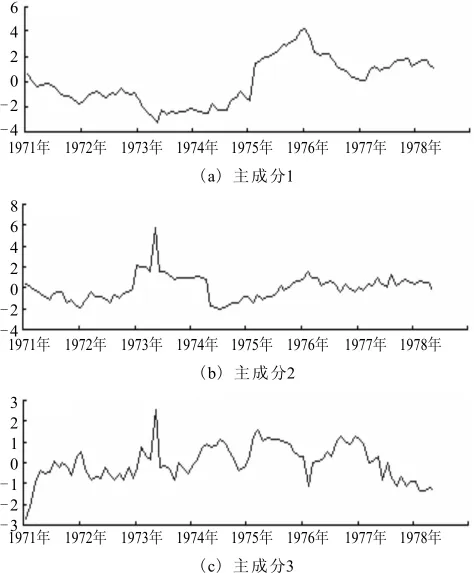
图4 主成分1、2、3分值曲线Fig.4 The value curves of the primary component 1,2and 3.
[1] 邵峰晶,于忠清.数据挖掘原理与算法[M].北京:中国水利水电出版社,2003:68-88.
[2] 王炜.主成分分析及地震活动参数的约简[J].地震学报,2005,27(5):524-531.
[3] 王炜.主成分分析法在地震预测中的应用研究[J].中国地震,2005,21(3):410-416.
[4] 陆远忠,阎利军,郭若眉.用于中短期地震预报的一些地震活动性参量相关性讨论[J].地震,1999,19(1):11-18.
[5] 韩渭宾.地震活动性参数分类及其相关性初步研究[J].四川地震,2003,(3):1-5.
[6] 李永振.应用RTL算法对岫岩MS5.4地震的回顾性预测[J].东北地震研究,2008,24(1):39-43.
[7] 王筱荣,李志海.新疆中强震预报的探讨[J].西北地震学报,2008,30(2):132-138.
[8] 李亚荣,何新社,陈军.甘肃及邻近地区中强地震前弱震空区的时空参数研究[J].西北地震学报,2008,30(3):293-297.
[9] 李永振,曹凤娟.主成分分析法在林甸MS5.1地震回顾性预测中的应用[J].东北地震研究,2008,24(2):29-34.
Application of Primary Components Analysis Method to Earthquake Prediction in Liaoning Province
LI Yong-zhen
(Earthquake Administration of Liaoning Province,Liaoning Shenyang 110034,China)
P315.51
A
1000-0844(2011)01-0076-04
2009-10-23
李永振(1976-),男(汉族),辽宁沈阳人,工程师,主要从事从事强震监测工作.
