基于有限元法光学材料热损伤的研究

刘效勇,卢佩,黄旭初,井群,唐光辉

(1石河子大学师范学院物理系/石河子大学师范学院生态物理重点实验室,石河子832003;2石河子大学信息科学与技术学院,石河子832003)

基于有限元法光学材料热损伤的研究

刘效勇1,卢佩2,黄旭初1,井群1,唐光辉1

(1石河子大学师范学院物理系/石河子大学师范学院生态物理重点实验室,石河子832003;2石河子大学信息科学与技术学院,石河子832003)

研究光学元件激光破坏的物理规律对改进激光系统及扩展其在科研生产中的应用具有重要意义。在考虑材料热力学参数随温度变化规律的前提下,以热传导方程和热弹方程为基础,采用有限元法,以 K9玻璃为例计算了空间高斯分布连续CO2激光辐照光学材料引起的温度和热应力分布及其熔融和热应力损伤阈值。

激光热损伤;有限元分析;热弹性理论;光学材料

大功率激光器的输出窗口材料和外光路中的透镜材料,如 SiO2、MgF2、K9玻璃、白宝石等在强激光辐照下,由于存在能量吸收和沉积可以在短时间内遭到破坏,容易导致光束质量降低而阻碍系统最优性能的发挥。因此,研究光学元件激光破坏的物理规律,提高其抗激光强度,对改进激光系统并扩展其在科研生产中的应用具有重要意义。

1 影响激光对光学材料损伤的因素

激光与光学材料相互作用是一个复杂的问题,影响因素主要有两个方面:一方面是激光参数对光学元件损伤的影响。材料在激光的作用下,由于破坏机理不同,将导致不同的破坏形态,损伤阈值也不同,材料最终以何种形态发生破坏,与辐照激光参数有密切的关系,如激光能量的高低,激光的波长、脉宽及激光光斑的大小及模式等,都是重要影响因素[1]。另一方面是光学材料物理参数对激光损伤的影响。由热应力所引起的光学材料的激光损伤可以用材料的抗热冲击阻抗 RH来表示[2]:

式(1)中:S为机械强度,k是热导率,α、E和v分别表示热膨胀系数、弹性模量和泊松比。

从式(1)可知:RH越大表示材料抗激光破坏的性能越好,激光损伤阈值越高。材料的激光损伤阈值与其热膨胀系数、热导率和机械强度等物理性质有较密切的关系。

2 理论模型

有限元法模拟计算的理论模型中,半高宽为 a的圆形空间高斯分布激光光斑照射在靶材中央,圆板形光学材料的厚度为 d,半径为b。由于整个系统轴向对称,故选用柱坐标系。坐标原点在材料的激光入射表面中心,z轴与激光照射方向一致。激光束垂直照射到样品表面(z=0)。t=0时刻激光开始照射样品,初始时样品温度均记为 T。样品激光入射表面、侧面绝热,底面有热辐射和空气的对流换热。根据热传导理论,圆柱坐标系下材料体内的温度场 T(r,z,t)分布遵从傅立叶热传导方程[3-5]:

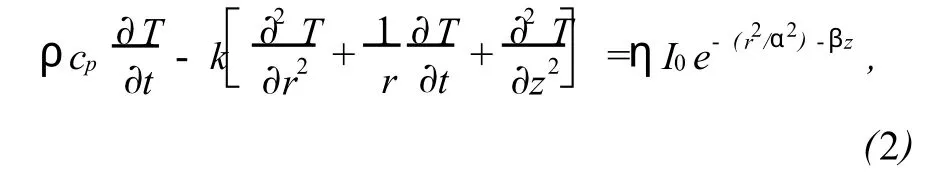
假定材料为简支状态,热弹性方程的自由边界条件可取为:

将热变形引起的等效载荷与边界条件处的外力等其它载荷项合并在一起,可求得包括热应力在内的综合应力。将由温度变化引起的热应变ε0作为初应变,由此可得弹性力学的应力-应变关系式:

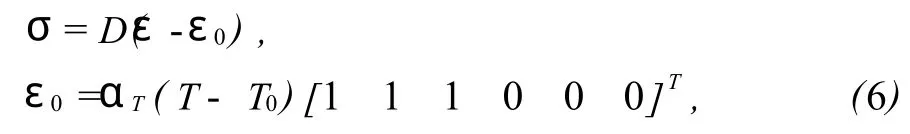
由虚位移原理可得用以求解热应力问题的最小位能原理的泛函表达式:

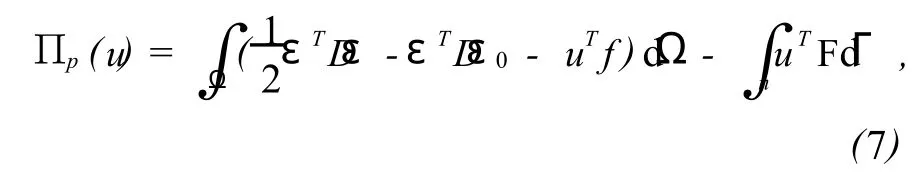
初始条件和边界条件分别为:

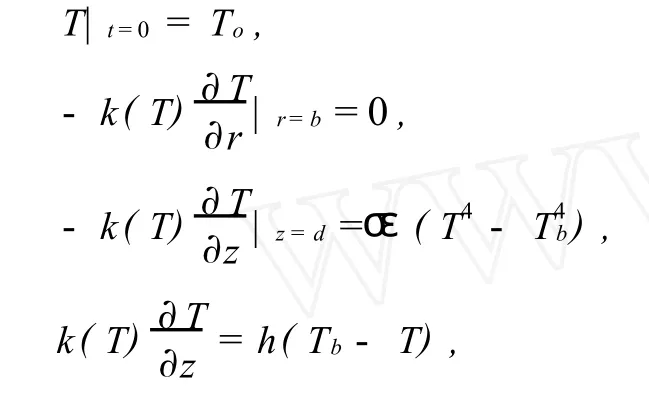
上式中:k(T)为材料热导率,ρ为密度,cp(T)为定压比热容,η为材料表面光热吸收率,β为材料吸收系数,b为材料半径,d为厚度,a为光斑半径,I0为入射激光的中心光强,σ是波耳兹曼常数,ε是表面辐射效率,Tb是外界环境介质温度,h为材料与空气的对流还热系数。

如果为三维轴对称模型,在忽略体积力和惯性力的前提下,材料体内的温度场发生非均匀变化时产生的热应变和热应力可用以下热弹性方程[6-8]来描述:

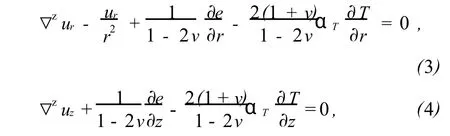
式(7)中:D为弹性矩阵,F为边界Γ上的面力分布函数,f为体积Ω内的体力分布函数,在忽略体力和惯性力的条件下,f=0。

对包括边界条件在内的全部求解域进行有限元离散,从δ Πp=0可得确定位移的矩阵方程:

式(8)中:为 KC结构整体刚度矩阵;aC为结构结点位移矩阵;PC为结构结点载荷矩阵,等于体积载荷、表面载荷及温度载荷三者之和。在材料体内温度场分布已知条件下,通过对矩阵方程式(8)的数值求解,即可完成对材料体热应力和热形变的有限元分析。

3 激光对K9玻璃热效应损伤的有限单元分析

式(3)、(4)中:ur,uz分别是(r,z)点的位移在 r、z方向上的分量;e为体应变;αT为热膨胀系数;υ为泊松比。

下面以 K9玻璃为例,采用有限元法计算空间高斯分布连续CO2激光辐照光学材料引起的温度和热应力分布,以及熔融和热应力损伤阈值。

K9玻璃的材料参量见表1[9-11]。Tmeit为材料的熔点,σth为材料的最大抗拉强度。材料的结构参量为:半径 b=1.5 cm,厚度 h=0.2 cm。CO2连续激光高斯光斑半径取为a=0.5 cm,中心光强 I0=256 W/cm2,η =0.85,ε=0.8,h=0.01 W/cm2K,取材料初始温度为 T0=190 K。

表1 K9玻璃材料的物性参量Tab.1 The physical parameter of K9

3.1 温升分析

图1给出了高斯光束照射 K9玻璃材料在t=6 s时温升的三维分布情况。

由图1可以看出:在激光入射表面中心处,温度最高,如果超过材料的熔点,材料就会发生熔融破

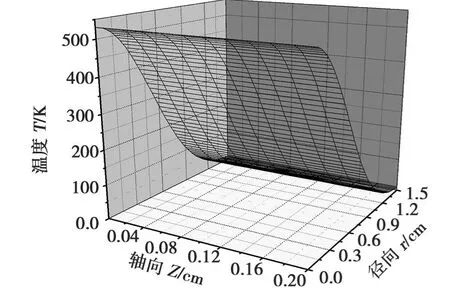
图1 t=6 s时温升的三维分布Fig.1 Elevated temperature distribution at t=6s

3.2 热应力分析

图3给出了高斯光束照射 K9玻璃材料在不同时刻材料表面(z=0)环向热应力的径向分布关系。

由图3可见:光斑中心区域温度高,称为“热区”,受热膨胀,表现为压缩热应力,为负值,在 r=0处压缩应力最大,随着材料半径的增加仍为负值,但绝对值减小。在远离光斑中心区域,温度基本不变,相对于“热区”可称为“冷区”,在“热区”与“冷区”交界处,环向热应力由负值变为正值,开始表现为拉伸热应力。在光斑边缘外侧附近达到最大值后逐渐下坏,这种破坏是由中心开始的。

图2给出了不同时刻在材料表面(z=0)温度的径向分布情况。

由图2可以看出:随着时间的增加,温度迅速上升,中心温度上升最快,时间越长温度升高越大。降。环向热应力最大值位置随辐照时间的增加逐渐向外偏移,最后基本稳定不变。

图4给出了不同时刻在材料表面(z=0)径向热应力的径向分布关系。

由图4可以看出:径向热应力始终为负值,其大小由中心向边缘逐渐减小到零。对于固体,通常材料的抗压强度(K9约690 MPa)远大于抗拉强度(K9约49 MPa),所以材料的损伤由环向热应力控制,即图中的正值部分,当最大环向热应力超过材料的抗拉强度后,就会发生解理破坏。

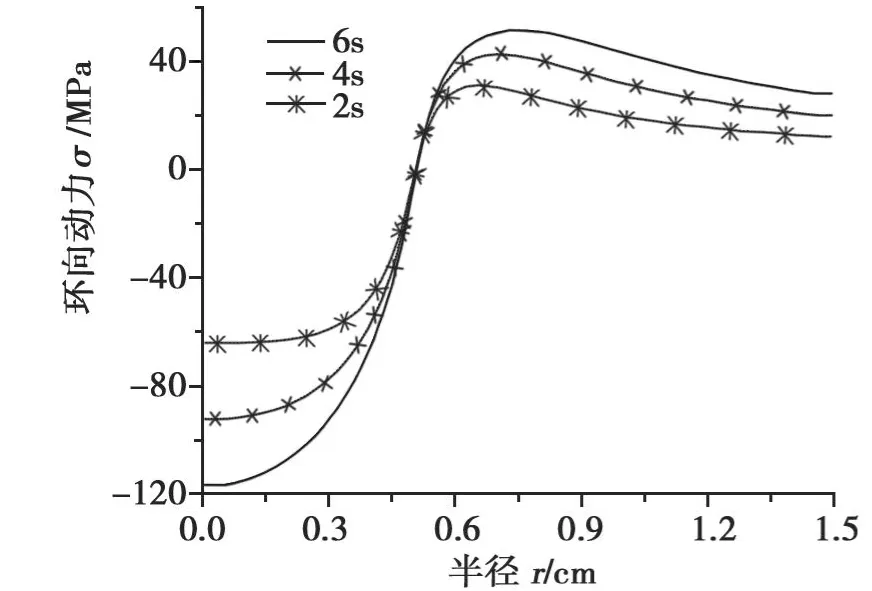
图3 不同时刻材料表面环向热应力的径向分布Fig.3 Circumferential thermalstress VS time

3.3 热损伤阈值和类型分析

连续激光照射光学材料时,损伤形态主要表现为超过材料的熔点而形成熔融损伤,或者是材料的热应力大于抗拉强度而解理破坏。

图4 不同时刻材料表面径向热应力的径向分布Fig.4 Radial thermal stress VS time

由上述分析可知,若是熔融损伤应出现在材料表面的光斑中心,如果是热应力损伤,应发生在光斑边缘外侧附近。图5表示的是 K9玻璃的熔融阈值和热应力损伤阈值与辐照时间关系。

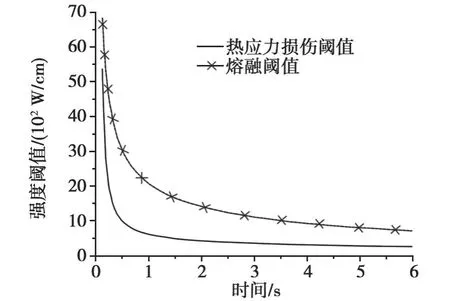
图5 K9玻璃熔融阈值、热应力损伤阈值与辐照时间关系Fig.5 Fuslon threshold VS danmage threshold and irradiation

由图5可知:在激光照射时间较短时,两种阈值功率都非常高,但随着时间的增加,曲线迅速下降,逐渐趋于平缓。K9玻璃的热应力损伤功阈值功率低于熔融损伤功阈值功率,所以损伤形态表现为炸裂或解理。

表2给出了不同功率连续激光照射 K9玻璃的实验结果[12],但未给出具体的玻璃半径及厚度。在此,利用本文的模型计算与之比较。当激光功率为274 W时,由本文模型计算得到的应力损伤时间为5.4 s,与实验中的6 s大体一致,这说明了该模型和结果的科学性。

表2 连续波激光器破坏实验结果Tab.2 Expermental results of CW laser damage

4 结语

本文以傅立叶热传导理论和热弹性理论为基础,运用有限元法建立了激光辐照材料的三维有限元数值计算模型,并以 K9玻璃为例计算了激光辐照光学材料引起的温度场和热应力场分布,得出了材料的热熔融损伤阈值和热应力损伤阈值,分析了材料的激光损伤类型,探讨了激光参数和材料性质对损伤阈值的影响。采用同样的理论方法,也可对强激光辐照下的半导体等非透明材料靶的熔融和汽化过程展开类似的研究,为激光对抗和激光加固提供理论参考。

[1]郭少锋,陆启生,程湘爱,等.光学材料的激光损伤形态研究[J].强激光与粒子束,2002,14(2):238-242.

[2]孙承伟.激光辐照效应[M].北京:国防工业出版社,2002:278-279.

[3]孙杨,李成富,张强.白宝石晶体的激光损伤[J].中国激光,1992(19):861.

[4]胡建平,马平,许乔.光学元件的激光损伤阈值测量[J].红外与激光工程,2006,35(2):187-91.

[5]Walker T W,Guenther A H.IEEE J.Quant.Electr,1981(QE-17):2053-2065.

[6]铁摩辛柯,古地尔.弹性理论[M].徐芝纶,译.北京:高等教育出版社,1990:252.

[7]巴斯著 KJ.工程分析中的有限元法[M].傅子智译.北京:机械工业出版社,1991.

[8]齐文宗,黄伟,张彬,等.红外连续激光反射镜热畸变的有限元分析[J].强激光与粒子束,2004,16(8):953-956.

[9]龚辉,李成富.连续CO2激光对红外窗口材料损伤研究[J].光学学报,1996,16(3):332-335.

[10]郭少锋,陆启生,邓少永,等.ns脉冲激光对 K9玻璃的破坏验[J].强激光与粒子束,2004,16(7):817-820.

[11]黄峰,牛燕雄,汪岳峰,等.光学窗口材料激光辐照热力效应的解析计算研究[J].光学学报,2006,26(4):576-580.

[12]夏晋军,龚辉,程雷,等.光学材料连续波激光热应力破坏效应[J].光学学报,1997,17(1):20-23.

Thermal Damage to Optical Material Based on Finite Element Method

LIU Xiaoyong1,LU Pei2,HUANG Xuchu1,Jing Qun1,Tang Guanghui1
(1 Key Laboratory of Ecophysics/Department of Physics,Teachers College,Shihezi University,Shihezi 832003,China;2 College of Information Science&Technology,Shihezi University,Shihezi 832003,China)

Under the prerequisite of considering the influence of temperature distributions to the thermodynamic parameters of the material,based on the thermal conduction equations and the thermal-elastic equations,the transient distributions of temperature and thermal stress in the optical material K9 is calculated by a finite element analysis method.Temperature and thermal-stress distribution,fusion and heat stress damage threshold figure of space Gaussian distribution when the CO2laser irradiation optical material are known clearly.The research on damage threshold of optical material by laser is very important to scientific research and production.

laser-induced thermal damage;finite element analysis method;thermal-elastic theory;optical material

O443;TP391 < class="emphasis_bold">文献标识码:A

A

2010-04-27

刘效勇(1976-),男,讲师,从事激光与光通信研究;e-mail:llxxyy1017@sina.com。