平面上有限级Dirichlet级数和随机Dirichlet级数的增长性

曹月波,倪科社

(石河子大学师范学院数学系,石河子832003)

平面上有限级Dirichlet级数和随机Dirichlet级数的增长性

曹月波,倪科社

(石河子大学师范学院数学系,石河子832003)

利用型函数及Newton多边形讨论了平面上有限级Dirichlet级数和随机Dirichlet级数的增长性和系数间的关系。通过引理得出:当时,Dirichlet级数的增长性和系数间的重要关系,以及对于随机变量序列满足条件:存在α＞0,使得snu≥p0E(|Xn|α) ＜ ∞;存在β＞ 0,使得的随机 Dirichlet级数 f(s,ω)和 Dirichlet级数有几乎相同的关于型函数的增长性。

Dirichlet级数;增长性;有限级;型函数;下级

ey words:Dirichlet Series;growth;finite-order;type-function;lower-order

这种级数是Dirichlet在研究数论时引进的。特别地,当λn=n,e-s=z时,Dirichlet级数变成了 Taylor级数,因此,Dirichlet级数可看做是 Taylor级数的推广。对Dirichlet级数增长性的研究具有重大的理论和现实意义。

Dirichlet级数的增长性和它的指数及系数之间有着密切的联系,在这方面国内外数学家作了大量研究[1～13]。其中,余家荣等[1]引入了概率中的一些重要结论和不等式,研究了满足一定条件的独立同分布的随机Dirichlet级数的收敛性和增长性;田宏根等[2,3]对平面上零级Dirichlet级数的增长性进行了研究;刘名生[4]对半平面上有限级Dirichlet级数的正规增长进行了深入研究得到了重要结果;罗仕乐[5]对半平面上无限级 Dirichlet级数与随机Dirichlet级数的增长性进行了研究;尚丽娜[6]对全平面上零级Dirichlet级数的增长性进行了研究;而金其余等[7]对左半平面上的无限级Dirichlet级数的上下级进行了研究。

本文对平面上有限级的Dirichlet级数及随机Dirichlet级数当时下级的情况进行讨论。

1 定义及引理

设Dirichlet级数

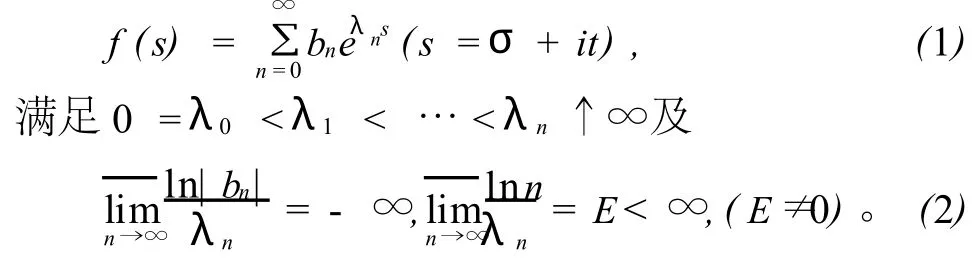
式(1)、(2)中{bn}为复数序列,σ和‘t为实变量。

级数(1)在全平面上是收敛与绝对收敛的,由它表示的函数 f(s)为一整函数。令称为级数(1)的级,称为级数(1)的下级 ,称υ(σ)为f(s)的最大项指标。

当级数(1)满足式(2)时,在oxy直角坐标平面上作点列,任取σ＞0,过点An作斜率为σ的直线与y轴的交点为y=-λnσ-ln|bn|,即取定σ＞ 0,L(σ)与 y 轴的交点越低,对应项的对数值就越大。因此,过最大项指标υ决定的点斜率为的直线的下方不会有{An}中的点。

记W(f)={最大项指标集合},H(f)={最大项指标决定的点集}。连接 H(f)中的点,得到一个以最大项指标决定的点为顶点的凸多边形Y(f),称其为牛顿多边形。∀σ＞0,斜率为σ的直线L(σ)与Y(f)相切,即 L(σ)在 Y(f)的下方 ,且与 Y(f)只有一个交点时,所过点的对应项必是最大项。L(σ)与Y(f)的一条边重合时,L(σ)上至少有{An}中的两个点都对应σ的最大项,但只有顶点对应的指标λn且n最大时才为最大项指标。

最大项指标是单调上升左连续的阶梯函数,记υ(σ)的间断点为它满足＞ 0,k=1,2,…,称{λNk}为最大项指标序列,且对应的点是 Y(f)的顶点。

本文中C表示常数,且先后出现表示不同的意义,不再一一说明。在以上规定下,本文得到以下关于平面上有限级Dirichlet级数的重要结果。

2017年12月，广东发改委就曾开展港珠澳大桥车辆通行收费标准听证会，对比当时的两个听证方案，最终正式公布的收费方案主要是降低了穿梭巴士的通行费，由原来的450元/车次降至300元/车次，这也大大降低了来往游客的消费标准。

引理1[1]在前述最大项指标及牛顿多边形的规定下,存在正整数 M,使当 k＞M时,有:

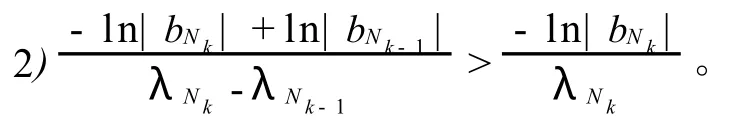
引理2[1]在条件(2)及前述最大项与最大项指标的规定下,有:

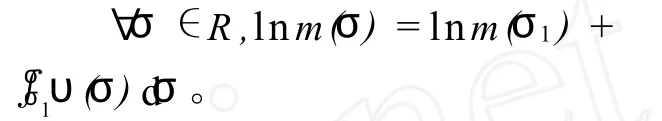
引理3[2]设Dirichlet级数(1)满足条件(2),则对有

引理4[3]设Dirichlet级数的级ρ为有限正数 ,引进函数 U(σ)=rρ(σ),其中ρ(σ)在σ≥σ0上非负、连续、单调,且满足=0;③对于任意正数

引理5设U(σ)是型函数,若Dirichlet级数满足(2),则

2 主要结果

定理1 设U(σ)是型函数,若Dirichlet级数满足条件(2)

而由型函数的性质知:对任意的ε＞0,当σ足够大时有:

对充分大的σ＞ 0,存在 k使得σ ∈[σk-1,σk),此时υ(σ)=λNk-1,故有

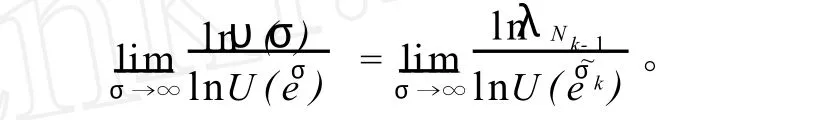
而由引理1知,存在正整数 M,使当 k＞ M时,有:

上述证明结合引理5可知本定理结论成立。

设随机Dirichlet级数

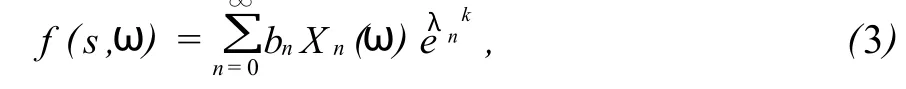
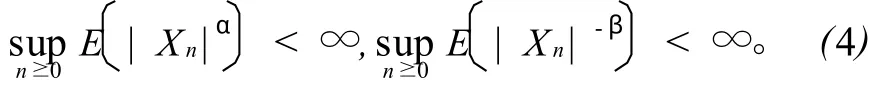
记 f(s,ω)的最大模和最大项分别为

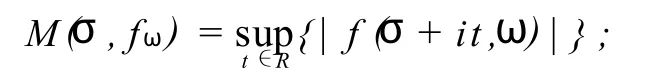
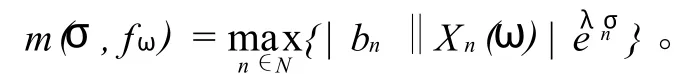
引理6若{Xn(ω)}是概率空间中独立复随机变量列,且满足式(4),则对存在 N(ω) ∈N,当 n ＞ N(ω)时,有

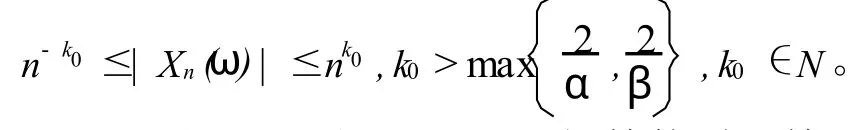
定理2设U(σ)是Dirichlet级数的型函数,随机变量序列{Xn(ω)}满足引理6的条件。若随机Dirichlet级数满足条件(2),则下式成立:

由引理6知,当 n充分大时,有

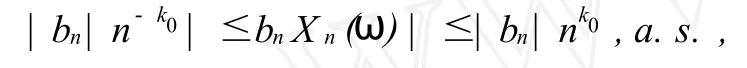
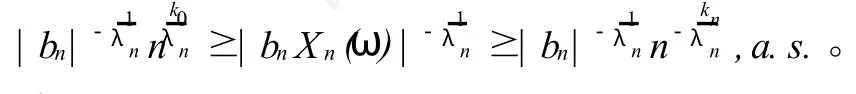
由以上讨论可知本定理2成立。

3 小结

研究有限级Dirichlet级数和随机Dirichlet级数关于型函数的下级是研究Dirichlet级数的一个重要方面。本文利用型函数及Newton多边形,对平面上有限级Dirichlet级数的增长性进行了研究,并得出了当时级数的增长性和系数及指数间的重要关系,得出了在 Xn满足一定条件下两类级数有几乎相同的关系型函数的增长性。

[1]田宏根,孙道椿,郑承民.平面上零级Dirichlet级数[J].系统科学与数学,2006,26(3):270-276.

[2]余家荣,丁晓庆,田范基.Dirichlet级数与随机Dirichlet级数的值分布[M].武汉大学出版社,2004:39-41.

[3]刘名生.半平面上有限级Dirichlet级数的正规增长[J].系统科学与数学,2002,22(2):229-238.

[4]罗仕乐,孙道椿.半平面上无限级Dirichlet级数与随机Dirichlet级数的增长性[J].数学物理学报:A辑,2009,29(2):475-485.

[5]尚丽娜.全平面上零级Dirichlet级数的增长性[J].数学的实践与认识,2007,37(18):151-154.

[6]Tian Hong-gen,Sun Dao-chun.The Growth of the Zero Dirichlet Series in Right Half Plane[M].Chin.Quart J of Math,2007,22(4):512-517.

[7]金其余,邓冠铁,郭晓晶.左半平面上的无限级Dirichlet级数的上下级[J].北京师范大学学报:自然科学版,2008,44(4):354-359.

[8]丁晓庆,刘军霞,孙华杰.整Dirichlet级数的增长性[J].西安工业大学学报,2007,27(6):588-590.

[9]曹月波,田宏根.双随机 Taylor级数的收敛性和增长性[J].济南大学学报,2008,22(2):203-205.

[10]HUO Ying Ying,SUN Dao Chun.The Growth of Random DirichletSeries[J].Journal ofMathematical Research&Exposition,2008,28(4):1027-1030.

[11]Sun Daochun,Yu Jiarong.On the Distribution of Values of Random Dirichlet Serie(II)[J].Chin Ann of Math:series B,1990,11(1):28-41.

[12]陈聚峰,刘名生.有限级Dirichlet级数及随机Dirichlet级数[J].数学物理学报:A辑,2005,25(7):965-973.

[13]杨祺.零级Dirichlet级数和随机Dirichlet级数的增长性[J].石河子大学学报:自然科学版,2008,26(2):261-264.

The Growth of Finite-order Dirichlet Series and Random Dirichlet Series on the Plane

CAO Yuebo,NI Keshe
(Department of Mathematics,Teachers College,Shihezi University,Shihezi 832003,China)

O174.52 < class="emphasis_bold">文献标识码:A

A

The relations between the cofficient and the growth of the finite-order Dirichlet series and random Dirichlet series on the plane are studied in the use of Newton polygon.It gains some lemmas and relations bettween the cofficient and the growth of the finite-order Dirichlet series whenr=eσ(σ→+ ∞),and further proves that the growth of random Dirichletis almost surely equal to the growth of Dirichlet serieswhen the random variable sequencesatisfies the condition: ∃α＞0 andβ＞0,making snu≥p0and snu≥p0K

2009-12-11

曹月波(1980-),男,讲师,从事复分析研究;e-mail:caoyuebo㊦tea@shzu.edu.cn。