关于炮弹运动方向、抽水做功辨析

陶印修

(天津渤海职业技术学院,天津市 300402)

关于炮弹运动方向、抽水做功辨析

陶印修

(天津渤海职业技术学院,天津市 300402)

对某高职高数教材的例题关于炮弹运动方向的处理展开研究,澄清导数的几何意义涉及到的角并非是炮弹运动方向中提到的角,而二者的正切值相等具有必然性,体现炮弹运动方向中正、负角的含义,品味正、负号的美,品味炮弹运动轨道方程;此外,还就几乎所有高数教材关于抽水做功的例题展开研究,澄清质量、重力(重量)、比重这些概念,揭示抽水做功的思想、方法。

方向;抽水做功;积零为整;微元法

数学在实际中如何应用,让我们来看下面两个问题.

一、炮弹运动方向问题与理想炮弹运动轨道方程

例1 不计空气阻力的情况下,炮弹以初速度 v0、发射角α射出,它的轨道由参数方程表示,t为参数.试求在任意时刻t炮弹的运动方向.解(书上的解法)这是一个抛物线方程(见图1).

用θ表示轨道的切线与水平方向的夹角,因此它刻画了炮弹运动的方向.则

图1

2.θ角与切线的倾斜角的联系

当炮弹往上运动时,θ角由发射角α逐渐减小,且θ角是正锐角,正号表示炮弹往上运动,到达顶点时θ角为零弧度的角β,此θ角是切线的倾斜角β,即;θ=β (2)

当炮弹往下运动时,θ角由零弧度的角逐渐减小,且θ角是负锐角,负号表示炮弹往下运动,虽然θ角不是切线的倾斜角β,但θ角与切线的倾斜角β之间满足:-θ+β=π,即θ=β-π. (3)

当炮弹往上运动时,根据(1)、(2)式,得当炮弹往下运动时,根据(1)、(3)式,得

需要强调的是,θ角既不是数学中两向量之间的夹角,也不是数学中关于直线的倾斜角,而是数学中有关的正、负角,体现了θ角逐渐减小的实际意义,即θ角由发射角α(正锐角)逐渐减小到零弧度的角(炮弹往上运动),再逐渐减小,θ角就只能是负锐角(炮弹往下运动),亦即正号表示炮弹往上运动,负号表示炮弹往下运动.关键问题是,“+”号表示“正方向”,“-”号表示“反方向”.在此也能体会到数学中关于正、负号的美.

4.理想炮弹运动轨道方程

实际上炮弹不是从地面上射出,而是从离地面一定的高度h处射出,因而炮弹的轨道方程应调整为

上面理想炮弹运动轨道方程把炮弹运动方向的数学模型作了调整,以期更符合实际.需要说明的是,h相对于炮弹上升的最大高度微乎其微,可以忽略不计,这就是例1.中为什么不加h的缘故;但对于投掷运动员来说,为提高运动成绩,就必须考虑投掷物出手的高度.

本文对炮弹运动方向问题研究可以深刻理解恩格斯所说的数学是什么的问题,即数学是关于数量关系及空间形式的科学,体会到数学中关于正、负号的美;本文对可忽略与不可忽略的情形作了简单介绍,体现数学在实际中如何应用.

二、抽水做功的问题

下面所用单位为国际单位.

1.抽水做功中应引起重视的几个基本概念问题

抽水做功中用到质量、重力(重量)、密度这些概念,由于诸多教材中的这些概念或多或少有问题,因此有必要澄清这几个基本概念.

首先看质量与重力的区别

质量是物体的属性,质量不会因物体所处的位置而改变,质量一般用 m表示,其国际单位为 kg(千克);重力是物体受其它物体(如地球、月球等)的吸引而受到的力,重力会因物体所处的位置而改变,重力一般用 G表示,其国际单位为 N(牛顿).

其次看质量与重力的联系

在地球上,物体的质量 m与重力G之间的联系为G=m g,而在月球上,物体的质量 m与重力G之间的联系为其中 g的国际单位为m/s2(米/秒2)或 N/kg(牛顿/千克),一般地取 g=9.8m/s2或 g=9.8N/kg.本文用到 g的国际单位为N/kg.

另外需澄清,重力才是物体的重量,重量不等同于质量,故唐国兴主编高等数学(二)第二分册在第185页上[例6.1]把质量写成重量不妥,应把重量改写成质量.

最后看比重

比重即密度.以前的教材用比重概念,而现在的教材用密度概念.

所谓密度,即单位体积的质量,而非单位体积的重力.密度的国际单位为 kg/m3(千克/米3).水的密度应为103kg/m3(单位体积的质量).故同济高数第四版教材在第360页上第一行把水的比重写成9.8 kN/m3(单位体积的重力)不妥.

2.抽水做功的计算

抽水做功的计算也用定积分来计算,其思想是积零为整,即把抽水过程实质上看成把一层层水分别提升到指定位置的过程;其方法是微元法,即将各层水抽出所做功的和,认为是泵抽水所做的功.

首先完善杨杰、丛金明主编书上第150页的例7(本文例2)

例2 半径为 Rm,高为 Hm的圆柱形水箱盛满了水,问要将箱内的水全部抽出要做多少功?

解 作 x轴如图2(原点选在水面圆心处,向下的方向为正方向),取水深度 x为积分变量,它的变化区间为[0,H].

图2

相应于[1,H]上任一小区间[x,x+d x]的一薄层水的高度为 d x,这薄层水的体积为πR2d x,质量为103πR2dx·g=103πR2gd x,重力为。把这薄层水抽出箱外需做之功近似地为 dW=103πR2gd x·x=103πR2gx d x,此即功元素.

于是所求的功为

说明一:例7的解把原点选在水底圆心处,向上的方向为正方向,未画出薄层水,其求解公式为W=103πR2(H-x)d x未推导;而例2的解把原点选在水面圆心处,向下的方向为正方向,画出薄层水,其求解公式为W=03πR2gx d x做了推导.

说明二:例7无单位(该书在第153页的习题5-4的第7题也无单位),其解中把质量当成重力(习题答案中也把质量当成重力),答案为π 2·R2H2;而例2补充了单位,其解中把质量与重力区分好,答案为

说明三:例2的解若也像例7那样,把原点选在水底圆心处,向上的方向为正方向,类似例2的解法,可得所求的功的公式,即

取水高度 x为积分变量,它的变化区间为[0,H].

相应于[0,H]上任一小区间[x+x+d x]的一薄层水的高度为 d x,这薄层水的体积为πR2dx,质量为103πR2dx·g=103πR2gd x,重力为.把这薄层水抽出箱外需做之功近似地为

dW=103πR2gd x·(H-x)=103πR2g(H-x)d x,此即功元素.

于是所求的功为

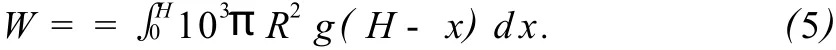
我们还可以证明(4)式与(5)式是等价的.

事实上,在(5)式中,设 H-x=y,则 d x=-dy,x=0时,y=H,x=H时,y=0。故

至此,(4)式与(5)式是等价的.

说明四:杨杰、丛金明主编高等数学在变力做功中只写了一个例题(本文例2),容易使读者误认为变力做功,但该例并非变力做功。

其次修正杨杰、丛金明主编书上第153页的习题5-4的第7题的答案(本文例3)

例3 半径 Rm为的半球形水池中贮满了水,要把这一池水抽到高为 Rm的水塔顶上,要做多少功?

解 作 x轴如图3(原点选在水面圆心处,向下的方向为正方向),取水深度 x为积分变量,它的变化区间为[0,R].

相应于[0,R]上任一小区间[x,x+dx]的一薄层水的高度为 d x,这薄层水的体积近似为π(R2-x2)d x,质量近似为103π(R2-x2)d x,重力近似为 103πg(R2-x2)d x.

把这薄层水抽出水池需做之功近似地为

dW=103πg(R2-x2)d x·(R+x)=103πg(R2-x2)(R+x)d x,此即功元素.

图3

最后完善阎章杭等主编书上第152页的例2(本文例4)之解

例4 修建一座大桥的桥墩时先要下围囹,并抽尽其中的水以便施工.已知半径是10m的圆柱形围囹的上沿高出水面2m,河水深18m,问抽尽围囹内的水做多少功?

原题的解中,把质量当成重力,需完善之.下面的解与原题的解仅此区别.

解 作 x轴如图4(原点选在围囹上沿处,向下的方向为正方向),取水深度 x为积分变量,它的

杨杰、丛金明主编书上第153页的习题5-4的第7题的答案为变化区间为[2,20].

图4

相应于[2,20]上任一小区间[x,x+d x]的一薄层水的高度为 d x,这薄层水的体积为π·102d x,质量为103π·102d x=105πdx,重力为105πgdx。把这薄层水抽出围囹外时,需要提升的距离近似为x,因此需做之功近似地为 dW=105πgx d x,此即功元素.

[1]胡农.高等数学[M].北京:高等教育出版社,2006.

[2]杨杰,丛金明.高等数学[M].山东:山东电子音像出版社,2002.

[3]唐国兴.高等数学(二)第二分册[M].武汉:武汉大学出版社,2000.

[4]阎章杭,刘青桂,张卫华.高等数学与工程数学[M].北京:化学工业出版社,2005.

[5]张顺燕著.数学的源与流[M].北京:高等教育出版社,2001.

[6]顾沛.数学文化[M].北京:高等教育出版社,2008.

[7]张顺燕著.数学的美与理[M].北京:北京大学出版社,2004.

[8]同济大学数学教研室.高等数学上册(第4版)[M].北京:高等教育出版社,1997.

[9]张顺燕著.数学的思想、方法和应用[M].北京:北京大学出版社,2003.

A bs tra c t:This article illustrates the author’s research on several controversial p roblems regarding shell’s movement direction and pumping w ork that appear in advanced mathematics course books and clarifies the concep ts such as the geometric meaning of derivative,quality,gravity and p roportion,and also reveals the idea and method of pump ing work.

Key word s:direction;pumping w ork;deposition of zero;infinitesimalmethod

Disc rim ination of Shells’Movem ent D irection&Pump ing Work

TAO Yin-xiu
(Tianjin Bohai Vocational Technical College,Tianjin 300201 China)

O 369

A

1673-582X(2011)02-0116-05

2010-10-15

陶印修(1963-),男,天津市人,天津渤海职业技术学院副教授,硕士,主要研究概率论与数理统计。