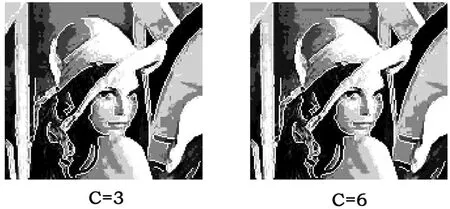基于蚁群模糊聚类算法的图像分割研究
2011-10-12李玉梅
李玉梅
(天津城市建设管理职业学院,天津市 300134)
基于蚁群模糊聚类算法的图像分割研究
李玉梅
(天津城市建设管理职业学院,天津市 300134)
论文提出了一种基于蚁群动态模糊聚类算法的计算机图像分割方法,有效地利用蚁群算法的聚类分析能力,克服了FCM算法对初始化的敏感,动态地确定了聚类数目和中心。然后利用蚁群聚类算法得到的模型进行修改,再进行模糊聚类弥补蚁群算法的不足。最后将该算法应用到计算机图像分割技术。对比实验表明,该算法实验表明该算法速度快、划分特性好,可以准确地分割出目标。
计算机图像分割;蚁群算法;模糊聚类
一、引言
本文用蚁群算法实现了基于改进的目标函数的模糊聚类,解决了动态确定聚类数目问题和防止遗传算法早熟现象的产生,并在计算机图像分割实验中验证了这一算法的有效性。
二、蚁群算法
蚁群算法是意大利学者M.Dorigo等人受自然界中蚂蚁觅食行为的启发而发展起来的一种新的模拟进化算法。该算法利用蚁群在搜索食物源的过程中所体现出来的寻优能力来解决一些离散系统优化中困难问题。蚁群算法的主要特点是通过正反馈、分布式协作来寻找最优解,这是一种基于种群寻优的启发式搜索算法,能根据聚类中心的信息量把周围数据归并到一起,从而得到聚类分类,最终得到最优解。
应用蚁群算法解决问题的一般步骤如下:
1.初始化:给各参变量赋初值,相当于蚂蚁匀在蚁巢,等待出发。
2.优化过程:蚂蚁根据给定路径长度和信息素强度做动态选择,并在运动中释放信息素。
3.路径决策:蚂蚁记录本次迭代的最佳路线。
4.终止条件:对于给定条件,若满足,则算法停止;否则,跳转步骤(2)。
三、模糊C均值聚类算法
模糊C均值聚类是模糊聚类算法中非常有效的一种,它能给出每个样本隶属于某个聚类的隶属度,即使对于很难明显分类的变量,模糊C均值聚类也能得到较为满意的效果。考虑一个样本集合X=[xij],其中:i=1,2,…,n;j=1,2,…,m;n代表所含的样本数,m代表每个样本中所含的变量数。此集合也可表示为:

式(1)中 ,xi={xj1,xj2,…xjm}j=1,2,…,m
将此集合依据一定的准则用模糊聚类的方法分成c个模糊子集,这里c为事先给定的聚类个数,所用的准则一般是某个用来表征聚类的性能指标的目标函数。模糊聚类的结果可用隶属度矩阵U来表示。U=[uij],uij的值在[0,1]之间,表示样本集合中的元素xj属于第i个聚类的程度,同时uij还必须满足:
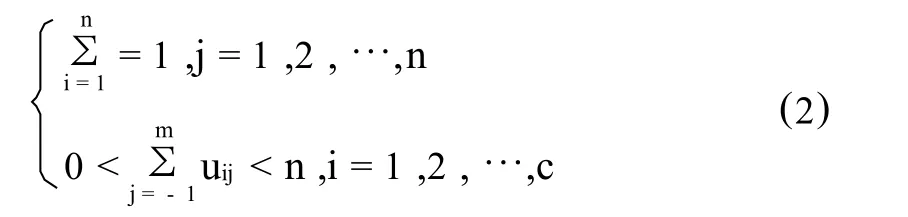
FCM算法的目标函数一般为:
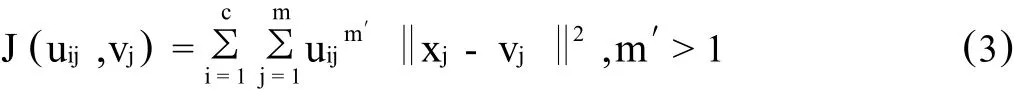
式(3)中,m′为影响隶属度矩阵模糊化程度的指数权重。
求式(3)的极小化问题,可得到uij,vj。
FCM算法提供了一种迭代算法来近似地得到目标函数的最优化值。
模糊C均值算法确定隶属度的具体步骤:
1.根据模糊聚类算法得到的类别数c作为分类个数,允许误差 Emax,t=1。
2.将利用蚁群算法得到的聚类中心点作为FCM初始化聚类中心wi(t),i=1,2,…,c。
3.计算隶属度 uij(t),t=1,2,…c;j=1,2,…n。
4.修正所有聚类中心wi(t+1),i=1,2,…,c。
如果e 蚁群算法主要是利用正反馈原理,当进化到一定代数后,就会由于最优路径的信息素不断增强而使蚂蚁大量聚集于少数的几条路径上,从而出现早熟、停滞现象。因此,单纯的蚁群算法并不能完全有效实现模糊聚类。另外,当聚类数与样本数相等时,显然FCM算法的目标函数为0,这已是最小值。这样,当聚类数不确定时就必须对目标函数改进用蚁群算法实现。应用蚁群算法与FCM算法相结合进行模糊聚类。一方面,蚁群算法的鲁棒性(稳定性)可以有效地克服FCM算法对初始化的敏感;另一方面,它的并行分布式计算可以加速收敛,提高聚类效率。最重要的是该算法的智能搜索和自适应特点可以达到全局最优。基于以上分析,用蚁群算法实现基于目标函数的动态模糊聚类的方法(AC-FCM算法)。 基于目标函数的动态模糊聚类的方法(AC-FCM算法)如下: 1.初始化 给定样本点集X={x1,x2,…,xi,…,xn} 迭代次数N,特征矢量维数m,聚类半径r,统计误差ε,各信息素τij(0)=0,初始中心V;计算dij= ‖xi-vj‖。 (5) 2.优化过程 (1)选择机制:每个样本点设置一个蚂蚁.设簇半径为r,计算各路径上的信息素,若dij≤r,则τij(t)=1;否则pij(t)=0.(t)表示t时刻蚂蚁i由 xi选择到vj的概率: 其中S={Xs|dsjΦr,s=1,2…,j,j+1,…N},为蚂蚁k下一步可以选择的样本点的下标的集合。ηsj(t)为t时刻蚂蚁i由xi选vj的启发信息,可取。α和β分别为残留信息和启发信息的重要程度. (2)更新机制 经过Δt时刻,,t=t+Δt,,l=l+1,完成一次路径搜索.则路径(k,i)的信息素更新为: 其中ρ:为0~1之间的常数,表示信息素的持久强度;1-ρ表示信息素的挥发程度。Δτij(t)表示第i个蚂蚁在时间t~t+Δt之间,在边(i,j)上的信息素改变量;Q是一常量,表示蚂蚁完成一次路径搜索所释放的信息素总量.然后计算新的聚类中心V和样本点到该新的聚类中心的距离dij。 3.路径决策 若pijΕp0,则 Xi归并到 Xj邻域。令Cj={xi|dkjΦr,k=1,2,…J},Cj表示所有归并到Xj邻域的数据集合。根据下式求出理想的聚类中心: 其中:Xk∈Cj。 4.终止条件 聚类中心的第i个分量。计算总体误差,再判断ε≤ε0是否成立。成立输出聚类个数c;若不成立,继续迭代。 为了检验AC-FCM算法的有效性,说明算法的性能,采用151 3 136的Lena(如图1)所示,作演示实验。实验环境为P4 3.0G,1G内存,操作系统为W indow s XP Professional,实验效果图采用Matlab7.0实现。取ρ=0.85,Q=100,N=50,ω=20,分别取C=3和C=6。蚁群算法图像分割结果如图2所示,AC-FCM算法图像分割结果如图3所示。 图1 lena图 图2 蚁群算法的结果 图3 AC-FCM算法的结果 实验结果表明,在聚类个数相同的情况,AC-FCM算法得到的图像处理结果比蚁群算法的处理结果轮廓更加明显,细节更加清晰,图像分割的效果更好,随着聚类个数的增多,更细微的边缘信息也可以被检测到。这说明算法使聚类表现出较优的效果,有较大地可信度。 [1]高新波.模糊聚类分析及其应用[M].西安:西安电子科技大学出版社,2004. [2]刘文,郑丽英.基于蚁群算法的模糊C均值聚类[J].太原科技,2009,(01). [3]Zhe Yan,Han-ming Gu.Research of the Image Segmentation based on Ant Colony A lgo rithm[J].2009 10th ACIS International Conference on Software Engineering,A rtificial Intelligences,Netwo rking and Parallel/Distributed Computing,106-109. A bs tra c t:This paper p roposes a method of computer image segmentation on the basis of the dy2 nam ic fuzzy clustering analysis of ant colony algorithm.The algorithm makes an effective use of the great clustering analysis ability,thus overcomes the sensitivity of fuzzy clustering method(FCM)to ini2 tialization and fixes the num ber and center of clustering dynam ically.Contrast tests show that this algo2 rithm is fast in calculation and accurate in target segmentation. Ke y w o rd s:computer image segmentation;ant colony algorithm;fuzzy clustering analysis Study on Com puter Im age Segm entation based on the Fuzzy Clustering A nalysis of A nt Colony A lgo rithm L I Yu-mei (Tianjin U rban Construction M anagement&Vocation Technology College,Tianjin 300134 China) O 29 A 1673-582X(2011)02-0078-04 2010-10-20 李玉梅(1962-),女,天津市人,天津城市建设管理职业技术学院助讲 ,从事计算机教学工作。四、蚁群模糊聚类算法
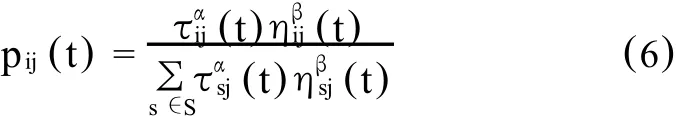
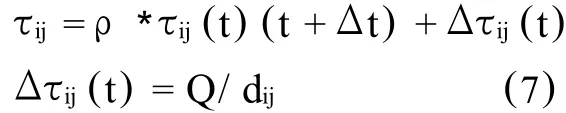

五、实验结果及分析