非加载边支持件对加筋壁板稳定性的影响研究

2011-10-11柯曾言

教练机 2011年1期

柯曾言,徐丹

(洪都航空工业集团，南昌 330024)

0 引言

加筋壁板是飞机翼面上常用的承力结构形式，当其用于翼面受压部位时，屈曲临界应力在很大程度上决定了该结构的承载能力，因此，最大限度地提高临界屈曲应力是整体加筋壁板设计的关键，但如何合理地考虑加筋壁板的边界条件是分析的难点。

目前，大部分参考文献[1-6]中，虽然加筋板的压缩局部屈曲系数最大可以达到约6.8，但在考虑纵向压缩总体屈曲系数时，非承载边的支持条件通常取简支，同时假设加筋条的扭转刚度很小，忽略了板沿加筋条轴线的扭转约束。因而，在估算总体屈曲应力时偏保守。实际结构中，大部分翼面在设计加筋壁板时，都有梁或墙对壁板的非加载边提供支持，不仅限制了壁板的边缘在壁板面内的翘曲，同时也限制了壁板绕壁板边缘（或梁缘条）的旋转。因此，筋条有一定的扭转刚度，在某些情况下，可以起到较强的抗扭作用。可以认为，板的边界实际上是具有某种程度旋转约束的弹性支持。

某型飞机机翼整体加筋壁板在详细设计阶段，有5块壁板的总体稳定性不能满足要求，但在静力试验时以上部位并未出现屈曲。本论文主要以该型飞机机翼整体加筋壁板为研究对象，考虑非加载边支持结构对屈曲应力的影响，总结了适合该型飞机机翼油箱壁板稳定性的计算规律。

1 典型加筋板结构参数

图1为某型飞机机翼整体油箱壁板典型结构。筋条有“工”字形和“Τ”字形两种形式。加筋板剖面示意图见图2，具体参数见表1。

图1 典型加筋板结构简图

加筋板材料及材料属性：7075T651，E=72400 MPa，v=0.33，ρ=2.796g/cm3，σ0.7=475.36MPα，压缩屈服应力，σcy=468.9MPα，σb=538MPα，形状参数 n=25。

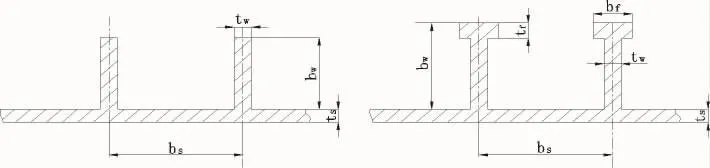
图2 加筋板剖面参数示意图

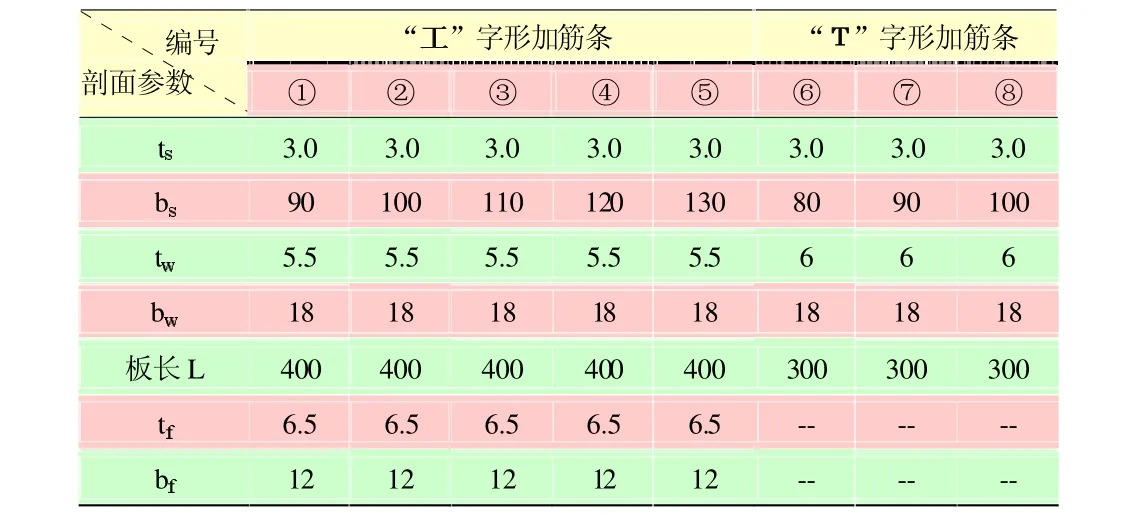
表1 典型加筋板参数（单位：mm）

2 有限元建模

2.1 模型简化

有限元建模时，将加筋板简化为壳元（shell），单元的长宽比为2～4，节点取在加筋板的中面上，有限元网格见图3。

考虑非加载边支持结构的屈曲模型是在图3有限元网格基础上，按支持件的实际参数，修改A-A'和B-B'边单元属性和增加支持件结构部分单元，有限元网格简图见图4，典型剖面见图5。

图3和图4中，A'-B'-C'-D'-E'-F'为加载端。

图3 非加载边无支持件的有限元网格简图

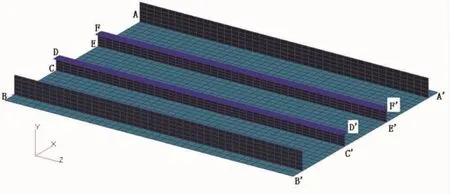
图4 非加载边有支持件的有限元网格简图

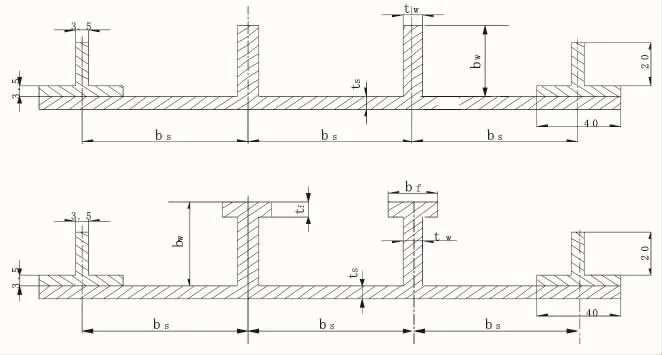
图5 非加载边有支持件的典型剖面

2.2 约束处理

u、v、w 分别为 x、y、z 方向的位移，θx、θy、θz分别为x、y、z方向的转角位移。

江小白1.0语录版，就是个人情绪、举动的碎片化表达。瓶身自带一句情绪型短句，如“关于明天的事，我们后天就知道了”，“低质量的社交，不如高质量的独处”等等，熟悉的鸡汤或反鸡汤式话语印在瓶身最醒目的位置，带给消费群体极大的情绪认同，也有人据称江小白为“情绪饮料”。

板端部 AB：u=v=w=θx=θz=0（边界简支）

筋条端部 C-D 和 E-F：u=v=w=θy=θz=0 （边界简支）

板端部 A'B'：u=v=θy=θz=0（Z 向可滑动简支）

筋条端部 C'-D'和 E'-F'：u=v=θx=θz=0（Z 向可滑动简支）

板端 A'-B'-C'-D'-E'-F'：w1=w2=w3……wn=……（所有节点的w相同，两端保持平面相对接近）

1）非加载边简化为“V”形槽支持

非加载边A-A'和B-B'：在板平面内可以自由弯曲，垂直板平面的位移v=0，垂直于非承载边方向的应力为0，即v=0，u≠常量。

2）非加载边弹性支持

非加载边A-A'和B-B'：在板平面内由支持件提供弹性支持，垂直板平面的位移v=0。

2.3 载荷处理

在加载端A'-B'-C'-D'-E'-F'上施加均布的压缩载荷，本论文在加载端单位面积（mm2）施加300N压力。

2.4 屈曲分析方法选取

基于MSC/NASTRAN的屈曲分析必须要有两种子情况：

第一子情况：定义载荷，进行静力分析。

第二子情况：选取特征值解法，求解屈曲分析的特征值问题。

本论文选取Lanczos法进行线性屈曲分析。

屈曲临界载荷：σcr=λ1·σ0，λ1—屈曲分析的最小特征值，由有限元屈曲分析得到。

2.5 有限元计算结果

MSC/NASTRAN软件中的Buckling模块，计算得各典型剖面的屈曲临界应力见表2，屈曲模态见图6～图 13。

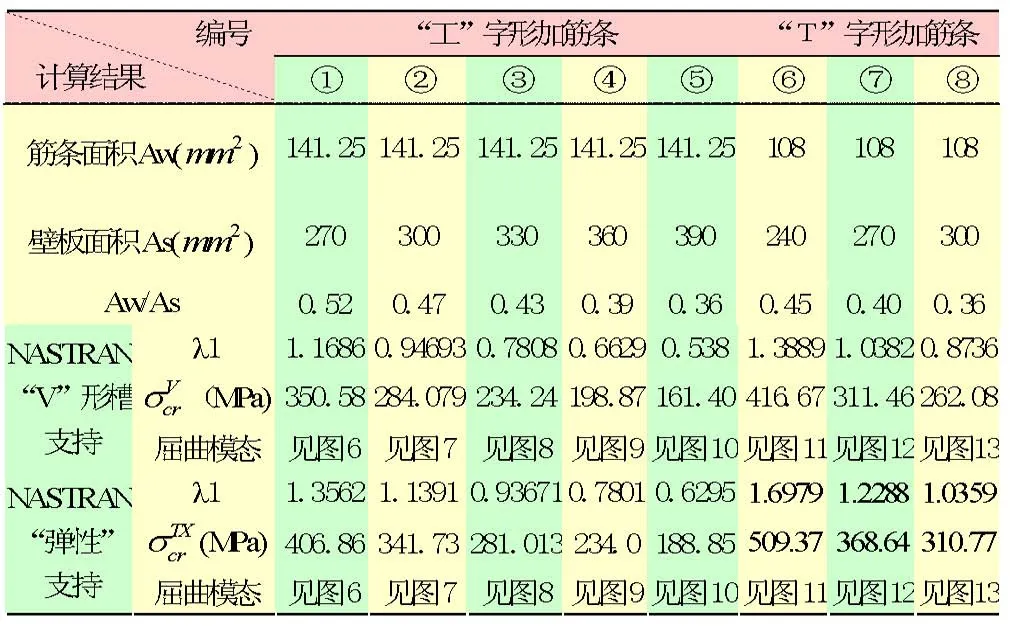
表2 各典型剖面的屈曲临界应力

图6 典型剖面①在两种边界条件下的屈曲模态

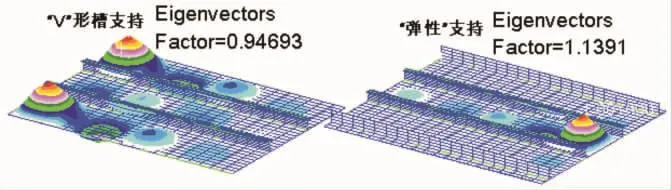
图7 典型剖面②在两种边界条件下的屈曲模态

图8 典型剖面③在两种边界条件下的屈曲模态

图9 典型剖面④在两种边界条件下的屈曲模态

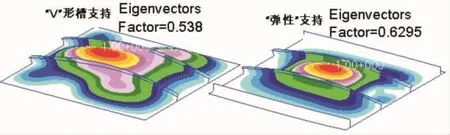
图10 典型剖面⑤在两种边界条件下的屈曲模态

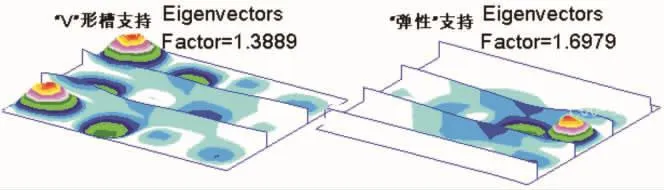
图11 典型剖面⑥在两种边界条件下的屈曲模态

图12 典型剖面⑦在两种边界条件下的屈曲模态

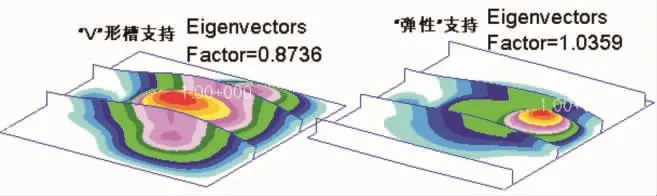
图13 典型剖面⑧在两种边界条件下的屈曲模态

3 计算结果及分析

工程中常用的稳定性分析方法主要使用结构稳定性设计与分析系统SDA1.1软件进行计算。计算得各典型剖面的屈曲应力及屈曲模式见表3。

由表2，各种典型加筋板在不同分析方法下的屈曲临界应力对比分析见表3及图14。

表3 各种典型加筋板的屈曲临界应力对比分析

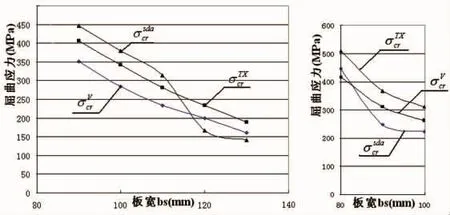
图14 不同分析方法下的屈曲临界应力变化曲线简图

由表3及图14可知：

当筋条面积和壁板面积之比大于0.4时，SDA1.1计算得到的屈曲临界应力较由MSC/NASTRAN计算得到的屈曲临界应力大；当筋条面积和壁板面积之比小于0.4时，SDA1.1计算得到的屈曲临界应力较由MSC/NASTRAN计算得到的屈曲临界应力小。用有限元法计算时，将支持件简化为“V”形槽支持和“弹性”支持对屈曲临界应力有明显影响，“弹性”支持情况的屈曲临界应力比“V”形槽支持情况的屈曲临界应力提高约16%～22%。由图6～图13，NASTRAN屈曲模态与SDA1.1的分析结果非常吻合，即当筋条很强时（Aw/As>0.4），发生局部塑性或弹性屈曲（受筋条约束的薄板屈曲）；当筋条较弱时（Aw/As<0.4），发生总体弹性屈曲（薄板和筋条同时屈曲）。