多媒体CAI课件的信息熵——评价CAI课件的一个量化指标

王翠香

中国地质大学信息工程学院，北京 100083

多媒体CAI课件的信息熵
——评价CAI课件的一个量化指标

王翠香

中国地质大学信息工程学院，北京 100083

通过随机变量的信息熵给出了评价CAI课件的一个量化指标,利用该指标可以从一个侧面评价CAI课件的优劣。

一 、引言

多媒体教学是信息时代一种全新的教学方式，多媒体课件的使用优化了课堂结构，提高了学习效率，已经成为教师进行课堂教学的重要手段和必然选择，因此，CAI课件的评价也成为一个亟须解决的重要问题。

CAI课件是一种信息的集合，我们主张CAI课件应该是一种面向问题型的CAI课件，而不应是一种课堂搬家、书本搬家，基于知识呈现的CAI课件。面向问题型的CAI课件充分反映了CAI的特点，有利于CAI学习的展开，有利于提高CAI的学习效果。课件中的问题不仅用于形成评价和结果评价，也可用于知识的呈现和传递，而学生对问题的应答是实现对学习过程控制的重要内容。课件的问题具有多种呈现方式，多项选择问题是使用最广泛的一种形式，其他的许多问题，如填空题等，往往也是以多项选择题的变形出现的，所以，对CAI课件中多项选择问题的评价在CAI课件的评价中占有重要的地位。以下通过CAI课件中多项选择问题的信息熵，给出了课件评价一个重要的量化指标。

二 、基本原理

熵是1865年作为热力学的一个重要概念引入的，在信息论中熵用来作为信息的度量。

设一个离散型随机变量X的概率分布为 P{X=xi}=pi，（i=1，2，…，n），函数称为随机变量X的信息熵或香农熵，简称为熵。显然，熵只与概率pi有关，而与随机变量的取值xi无关。

随机变量熵的大小可用于表示概率系统的不确定程度。

设在一概率系统中，每一事件发生的概率分布为：（0，…，0，1，0，…，0），它表示该系统中的某一事件发生的概率为1，其他事件发生的概率为0。这是一个确定系统，不确定度为0，计算该系统的信息熵，得H=0。

如果其概率分布是均匀的，即（1/n，1/n ，…，1/n），它表示系统中的每一事件发生的概率相等，我们很难预测哪一个事件发生，这种系统的不确定性最大。可以证明以下的定理[1]：对于离散型随机变量，当其可能的取值等概分布时，其熵达到最大值，且

Hmax（X）=log2n，其中n为X可能取值的个数。

由于信息熵的大小不仅与系统的概率分布有关，还与系统所包含事件的个数n有关，不利于对不同系统的信息熵进行比较。为了有效地比较不同系统的信息熵，对信息熵进行标准化，得到相对信息熵：H*= H/ Hmax。

设系统的概率分布为（p1，p1，…，pn），则相对信息熵为

相对信息熵使得的熵的计算归一化为标准的范围0～1之间，它使得不同系统的信息熵易于比较。

三 、CAI课件评价的一个量化指标

在课件的制作中，问题的设计十分重要，特别是对于面向问题型的CAI课件更是如此。问题的信息量，对课件的评价具有重要意义。从问题、课件所具有的学习功能来看，问题的信息量越大，表示学生的应答分布的分散性越大；问题的信息量越小，表示学生的应答分布的越集中。

例如，对于有5个预选答案的多项选择题，学生的应答的概率分布可能有多种不同的情况：

（1）（1，0，0，0，0）

计算相应的应答信息熵

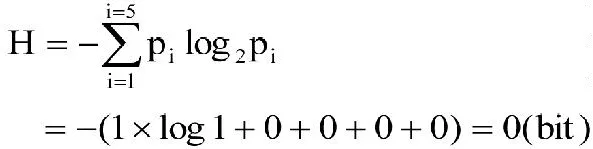
（2）（0.5，0.5，0，0，0）

计算相应的应答信息熵

（3）（0.5，0.125，0.125，0.125，0.125）

计算相应的应答信息熵

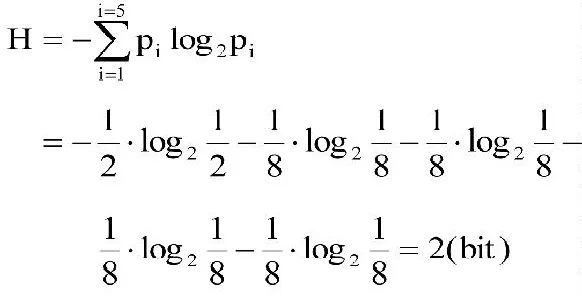
（4）（0.2，0.2，0.2，0.2，0.2）

计算相应的应答信息熵

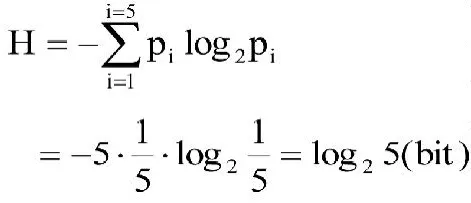
对于应答情况（1），这种应答概率分布的信息熵为零，它表示学生的应答全部集中在第一个预选答案，显然学生在回答这样的问题时，可以不做更多的思考，从学生的学习来看，这种问题不是很好的问题。

对于应答情况（4），这种分布具有最大的信息熵，它表示学生的应答选择十分分散，这样的问题具有较大的“迷惑性”，学生在选择应答时，需要进行认真的思考才能得出结论，这样的问题可以促使学生进行深入地思维，对于课件而言，这是一个很好的问题。（2）和（3）是介于（1）、（4）这两种情况之间，而情况（3）中的问题比（2）中的问题要好。

基于以上的分析，我们可以使用信息熵来评价课件中所设置的问题，从促进学生认真思考，产生较好的学习效果来看，信息熵高的问题优于信息熵低的问题。

为了便于不同的课件相互比较，我们给出以下的定义[2]如果某一课件包含N个多项选择问题，称

为课件中这些问题的平均相对信息熵。

综上所述，信息熵的大小完全由CAI课件本身所决定，没有涉及人为的因素，是客观公正的，因此信息熵可以作为对CAI课件进行评价的一个重要的量化指标。

[1]朱雪龙 编著.应用信息论基础.清华大学出版社.2002年12月

[2]傅德荣，章慧敏 编著.教育信息论处理.北京师范大学出版社.2001年9月

The Information Entroy of the CAI——The Assessment Index of the CAI

Wang Cuixiang
China University of Geosciences, School of Information Engineering, Beijing 100083,China

In this paper we obtain a quantitative index of the assessment of the CAI by information entroy. We can use the index to judge that the CAI is good or not.

10.3969/j.issn.1001-8972.2011.02.042

王翠香 女 副教授，主要从事应用数学的研究。

CAI课件；信息熵；评价指标

CAI；Information Entroy；Assessment Index