三次NURBS样条曲线插补加工螺旋转子建模与加工研究*
2011-09-29余道洋
余道洋 韩 江 夏 链
(合肥工业大学机械与汽车工程学院,安徽合肥 230009)
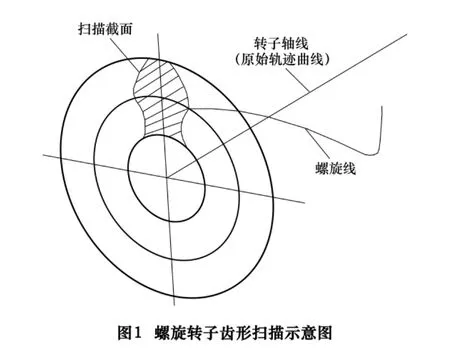
螺旋转子流量计是20世纪90年代末新推出的一种新型流量计,它具有如下优点:动平衡良好,振动及噪声小,体积小,计量容量大;不产生脉冲;转子表面无负荷,在旋转过程中不产生磨损,使用寿命大大延长[1]。螺旋转子是其中最关键的零件,其端面轮廓齿形截面如图1所示。
螺旋转子端面轮廓曲线由3段曲线组成:渐开线、摆线和圆弧。圆弧可以由数控系统圆弧插补来实现,渐开线和摆线现在一般采用微小直线段来拟合实现。但是,微小直线段不仅代码量非常巨大,而且直线段间的不连续破坏了曲率的光滑性,会导致速度加速度的不连续[2],存在加工效率低的问题,在四轴加工中心上加工模数为13.5 mm的螺旋转子需要3 h,加工模数更大的螺旋转子需要更长加工时间,有的甚至需要20 h以上。要克服这些不足,提高加工效率,必须采用自由曲线插补。本文提出用三次NURBS样条插补来拟合渐开线和摆线,大大提高了加工效率。
1 三次NURBS曲线构造与计算
1.1 构造三次NURBS曲线
本文以端面轮廓其中摆线段为例,说明三次NURBS曲线的构造过程。三次NURBS曲线可以表示为1个分段有理多项式矢函数。
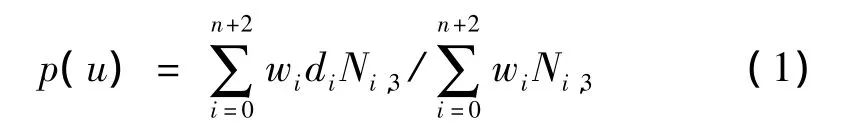
式中:型值点个数为n+1;控制顶点为di(i=0,1,…,n+2),其顺次相连构成控制多边形;wi为与控制顶点di相对应的权因子;Ni,3是3次B样条基函数。
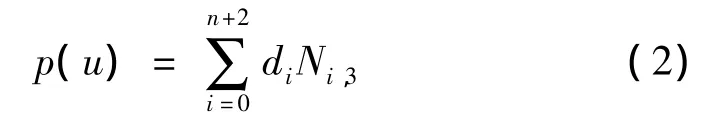
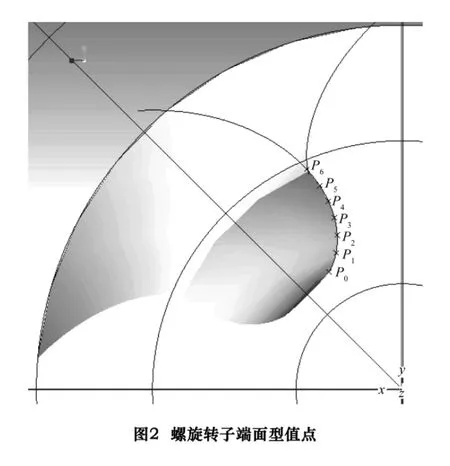
图2是螺旋转子端面轮廓曲线摆线上的7个型值点(本文中设n=6),型值点坐标如表1所示,求通过这些点的三次NURBS曲线。
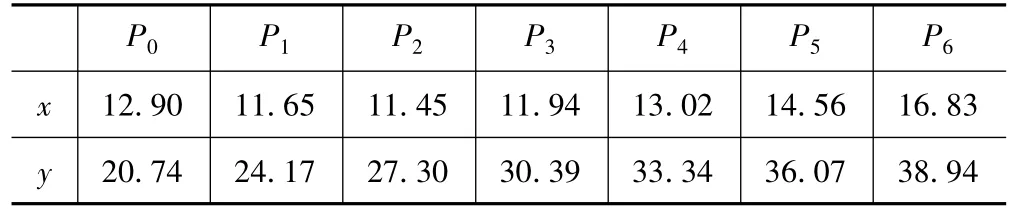
表1 NURBS曲线上型值点的坐标
1.2 确定节点矢量
根据曲线上的型值点 pi,i=0,1,…,n(n=6),采用平方根法确定节点矢量。设7维矢量a=(a0a1…a6),求得a的各个分量如表2所示。
根据式(2),两端采用四重节点,构造n+7(即13)维节点矢量
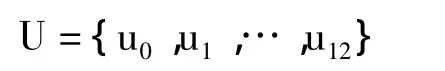
分别在曲线两端构造4次重节点,即u0=u1=u2=u3;u9=u10=u11=u12,求得各分量的值如表3所示。
1.3 计算基函数
采用 De Boor-Cox递推算法[3],
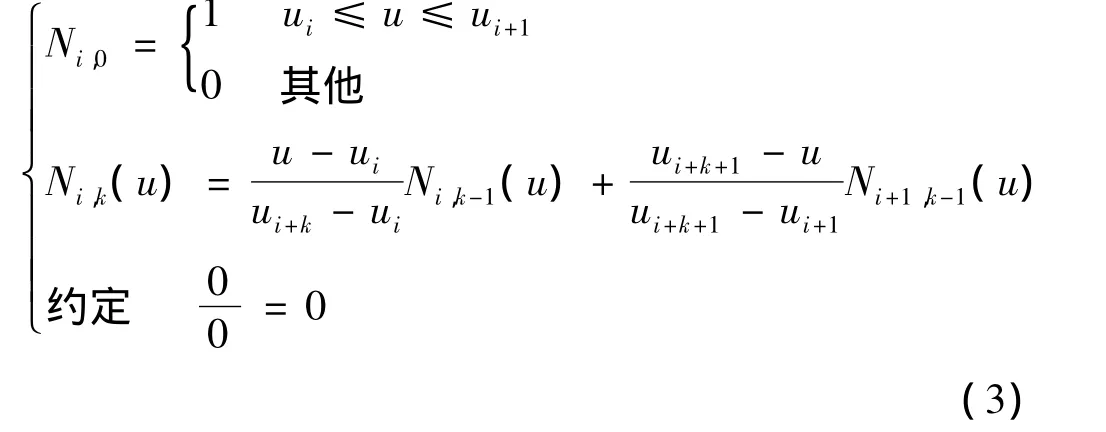
计算时需分别求出0、1、2、3次B样条基函数,亦即将k=0,1,2,3依次代入公式,通过递推关系计算得三次B样条基函数。由于篇幅关系,本文只列出三次B样条基函数。三次B样条基函数为:
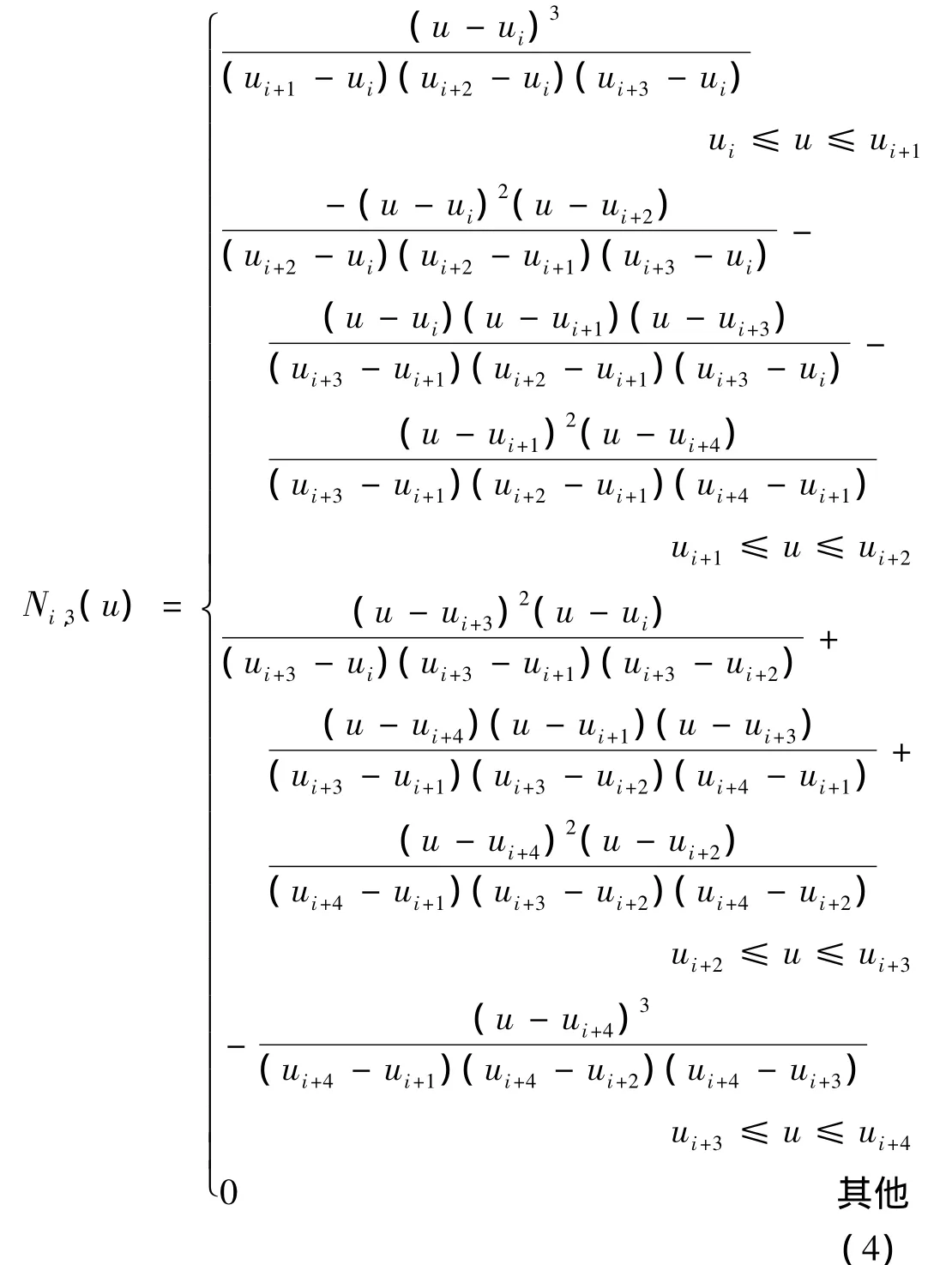
1.4 反求控制顶点
用于拟合n+1 个型值点pi,i=0,1,…,n的三次B 样条曲线可表示为[4-5]:
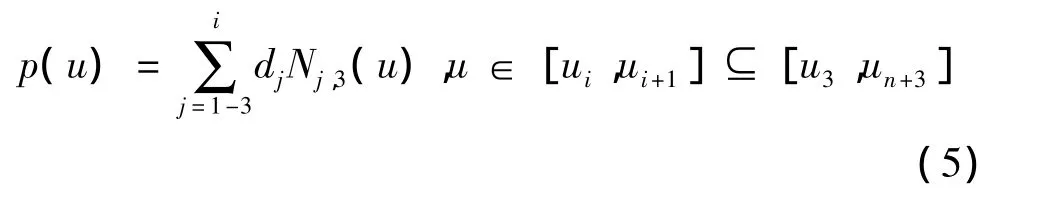

表2 7维矢量a各分量值

表3 节点矢量各分量值
将定义域u∈[u3,un+3]内的节点值依次代入式(5),有
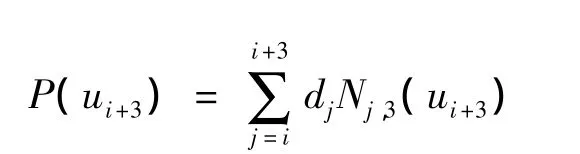
取n=6,结合边界条件可求解;设NURBS曲线的控制顶点 d0、d1、d7、d8和NURBS相切,从而可以求出控制顶点的坐标,如表4所示。
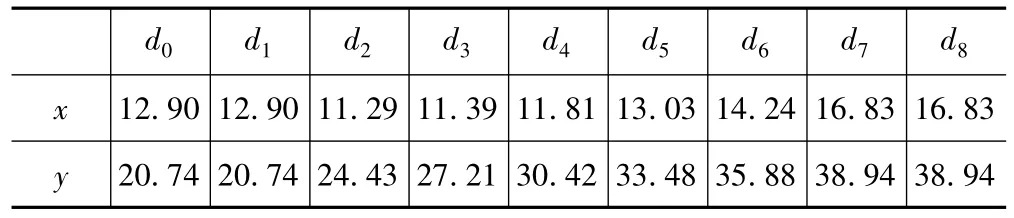
表4 控制顶点的坐标
2 计算三次NURBS样条曲线插补刀位数据
由于大多数高端数控机床都具有刀补功能,计算出三次NURBS样条曲线的基函数和控制顶点后,可以直接用这些点的数值进行编程[6]。
由式(5)可知:
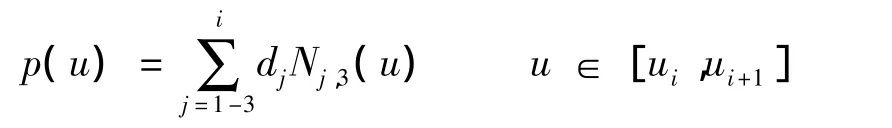
由1.3节已求出Ni,3,由 1.4节已求出控制顶点的坐标,设i=3时,即u∈[u3,u4]时,可以用三次NURBS样条曲线来拟合求出螺旋转子端面轮廓摆线段其中一段:
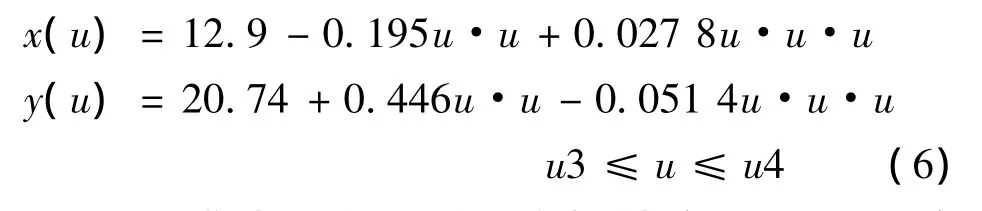
同理可求出其他几段,这样就实现了用三次NURBS样条曲线来拟合端面轮廓摆线段。
由三次NURBS样条曲线性质[7],经过矩阵变换,将式(6)变换成数控系统所需要的三次样条曲线插补方程,就实现了用三次样条插补加工螺旋转子端面轮廓摆线段。
3 刀位数据模拟与误差分析
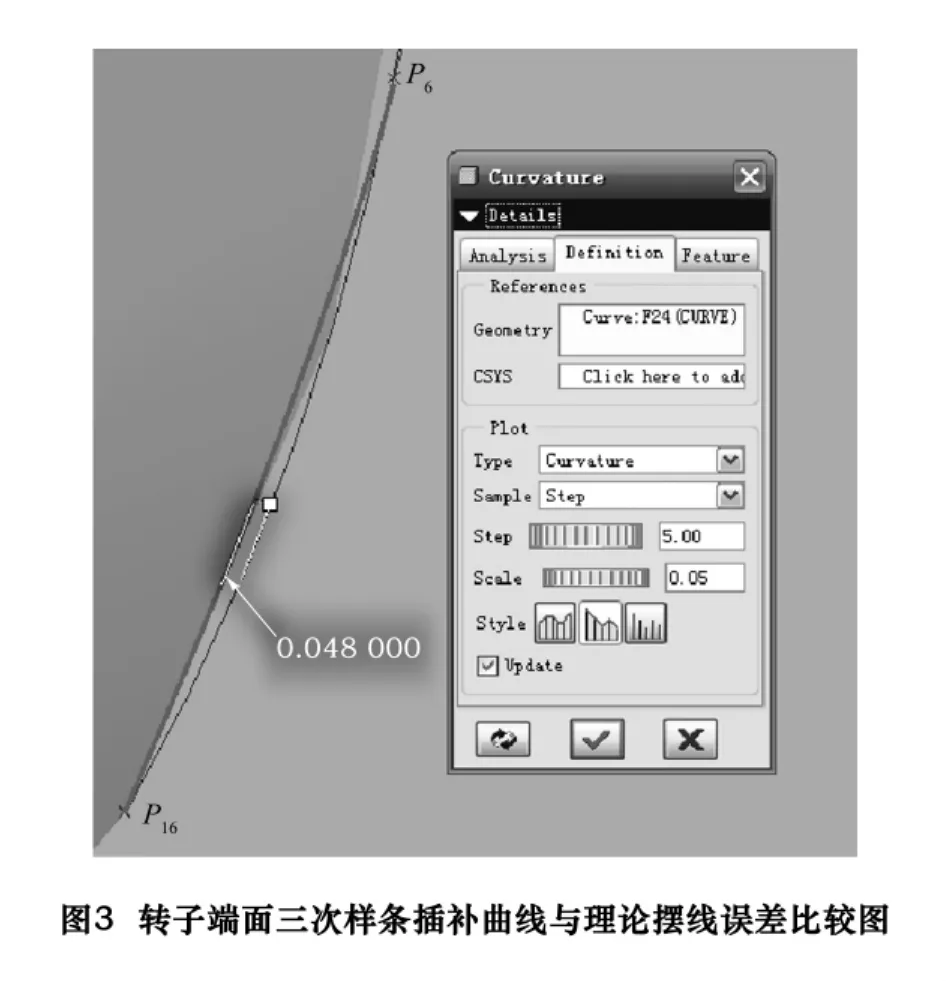
将式(6)输入到Pro/E软件中,结果如图3,细线条表示理论摆线轮廓,粗线条是式(6)表示的三次样条曲线的拟合曲线,经过分析比较三次样条插补曲线与理论摆线误差后得出,最大误差为:0.048 mm,小于螺旋转子的加工制造允许误差范围。同理可以分析比较其他几个三次样条曲线的拟合曲线和理论摆线轮廓误差,经过分析计算,轮廓曲线误差都在允许的误差范围之内。
4 在加工中心上加工验证
螺旋转子的实际加工运用立式四轴加工中心进行数控铣削加工。经过实际加工试验,采用三次NURBS样条曲线插补加工螺旋转子,比采用微直线段插补加工螺旋转子大大提高了螺旋转子的加工效率,在保证螺旋转子制造加工精度的前提下,可以提高螺旋转子的加工效率50%以上。同时,本文采用的三次NURBS样条曲线插补加工方法对于加工一些特殊曲线和曲面也具有一定的借鉴意义。
[1]余道洋,韩江,夏链.螺旋转子数控加工的数学建模分析与研究[J].合肥工业大学学报,2007,30(11):1433 -1435.
[2]李建刚,张婷华,李泽湘,等.数控加工中的连续多段直线轨迹B-Spline拟合[J].哈尔滨工业大学学报,2008,40(10):1606-1608.
[3]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[4]王乾廷,桂贵生,刘全坤.三次NURBS曲线轮廓数控加工刀位数据计算[J].组合机床与自动化加工技术,2003,6:19 -21.
[5]俞芙芳,王乾廷,江吉彬.鞋楦曲面混合有理Bezier构造及刻楦过程仿真[J].机械工程学报,2005,16(21):1899 -1903.
[6]WANG Yongzhang,CHEN Liangji.A real- time NURBS surface interpolator for 5 - axis surface machining[J].Chinese Journal of Aeronautics,2005,18(3):263 -272.
[7]吉贝·德芒热,让皮尔·晡热.曲线与曲面的数学[M].北京:商务印书馆,2000.
