多孔介质中溶质弥散传输过程的体积微元建模法
2011-09-28王长江姜汉桥覃生高李俊健
王长江,姜汉桥,覃生高,李俊健
(1.中国石油大学石油工程学院,北京102249;2.东北石油大学石油工程学院,黑龙江大庆163318)
多孔介质中溶质弥散传输过程的体积微元建模法
王长江1,姜汉桥1,覃生高2,李俊健1
(1.中国石油大学石油工程学院,北京102249;2.东北石油大学石油工程学院,黑龙江大庆163318)
用体积微元法推导出考虑吸附效应的对流弥散新模型,分析HLL模型和理想对流弥散模型的简化条件,通过与马尔科夫方法的推导结果对比,确定出体积微元法建模过程与简化条件的随机统计特征。两种方法中,对流流量中颗粒的俘获项对应漂移变量的空间导数,弥散流量中颗粒的俘获项对应扩散变量的空间导数。结果表明:渗滤系数越大,颗粒浓度越高,弥散率越大,发生吸附的颗粒概率密度越大;多孔介质孔隙度越小,弥散颗粒样本路径越小,发生吸附的颗粒概率密度越大。
体积微元法;对流弥散方程;马尔科夫方法;颗粒俘获
地下水运移过程中,溶质颗粒分子扩散和机械弥散综合作用的结果使得弥散前沿为非均匀的过渡区域,并向前移动[1-2]。对这一过程进行数学描述和求解是水力学和渗流力学研究中的一项重要内容[3-5]。Fick通过试验方法得出了描述稳态扩散的第一定律,并导出了描述非稳态扩散的第二定律。J.E.Altoé F等[6]针对Iwasa[7]构建的模型没有考虑水动力弥散的不足,根据悬浮颗粒的物质平衡方程,在颗粒俘获动力学方程中考虑对流弥散效应,建立了较完整的深层渗滤数学模型。葛家理等[8]利用体积微元法分别推导了理想条件下和考虑实际黏度差及吸附效应的对流弥散微分方程。同时,溶质颗粒的对流弥散具有统计行为特征,弥散前沿颗粒的浓度分布是大量粒子随机游动累积的结果。J.E.Altoé F[6]建立的深层渗滤模型明确从颗粒俘获概率的角度考虑储层损害,葛家理[8]的理想对流弥散方程浓度分布即为一概率解。王子亭等针对对流弥散的Cauchy问题的积分形式,建立了相应的随机微分方程并论述其存在唯一马尔可夫解的条件。但是,目前尚没有多孔介质中溶质颗粒弥散传输的体积微元建模方法及其概率统计意义的报道。笔者根据描述马尔可夫链转移概率的查普曼柯尔莫哥洛夫方程,推导考虑吸附效应的对流弥散控制方程,并与体积微元法推导过程对比,论证随机理论对描述多孔介质传质过程方法的有效性。
1 对流弥散方程的体积微元法推导
假设一单位截面积的体积微元,溶质颗粒浓度较低时,悬浮液密度和孔隙度为常数,悬浮颗粒和沉积颗粒的平衡方程[6]为

式中,c为单位体积流体内悬浮颗粒数;σ为滞留颗粒浓度即单位体积岩石捕集的颗粒数;φ为孔隙度;q为总粒子流量。
颗粒流量q由对流和弥散两部分组成,即

其中

式中,D'为视弥散系数,与流速u成比例;αD为弥散率。
考虑颗粒的吸附效应(图1),在流体通过孔隙体积时,颗粒没有被俘获,但在垂直于流体流动方向上存在一系列颗粒捕集筛。任一粒子被俘获的概率是λl(l为筛间距,λ为渗滤系数,指多孔介质中俘获速率与总的粒子流量的比例系数,颗粒孔隙尺寸比越大,λ越大),通过的概率是1-λl,且俘获速率与总粒子流量成比例[10],一颗粒被孔隙俘获,不管是对流还是弥散流将其携带到孔隙边,

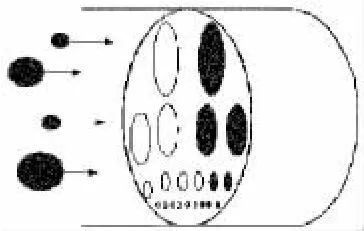
图1 颗粒在孔隙被俘获Fig.1 Particles captured in pores
对式(2)求导,假设在该局部流动时u和D'为常数,有

将式(2)代入式(3),则

将式(4),(5)代入式(1),认为孔隙度为常数,令v=u/φ,D=αDv,则

忽略颗粒俘获方程(2)中的弥散项,即只考虑对流流量中粒子的俘获效应,忽略弥散流量中粒子的俘获效应,则式(6)成为HLL模型[11],即

如忽略方程(1)中粒子的俘获效应,则式(6)变为理想对流弥散模型[8],即

2 考虑吸附的对流弥散过程的随机建模
假定由均质砂粒制成的圆管模型中开始时充油,从某时刻t=0开始,用含有一定浓度(c0)的化学剂进行驱替,初始时刻(t=0)两种液体的界面位于x=0处,在此界面的左侧驱替剂浓度c=c0,而在右侧(即岩心中),驱替剂的浓度c=0;t>0某时刻模型中的浓度分布示意图如图2所示。

图2 弥散流动模型中驱替剂浓度分布Fig.2 Concentration distribution of displacement agent in dispersive flow model
溶质由水携带自注入端向出口端运移,t=0为初始时刻,此后任一时刻t>0,溶质粒子所在的位置是一维随机变量(ξt,t≥0),t在参数集T∈[0,∞]中变化,对应一随机过程,记为{ξt,t≥0}。若已知ξs=y,由于孔隙通道的随机性及溶质粒子的随机运动,ξt(t>s)的分布与s以前过程的取值无关,由马尔可夫过程的定义可知,{ξt,t≥0}是马尔科夫过程,以F(x,t;y,s)=P(ξt≤x|ξs=y)表示它的转移概率分布函数。设f(y,t;x,s)为转移概率密度,则由于溶质在多孔介质中移动存在弥散现象,可以假定对于任意ε>0,Δt>0,f(y,t;x,s)满足下列3个条件:

式(9)表示t时刻自y出发的溶质粒子经Δt后运移出区间(y,x)的概率是比Δt更高阶的无穷小,这反映溶质粒子在孔隙通道中在很短的时间内不能得到很大的位移,即粒子为连续性运动;

在条件(9)下,分析式(10)和式(11)中的A(y,t),B(y,t)的概率和物理意义可知,A(y,t)为在t时刻自y出发质点的瞬时平均速度,B(y,t)与平均波及面积相联系。于是,{ξt,t≥0}是扩散过程,则微分查普曼-柯尔莫哥洛夫方程简化成为福克-普朗克方程,一维条件下的表达式[11]为

相应的过程在数学上称为扩散过程。A(y,t)称为漂移变量,B(y,t)称为扩散变量。在多维空间的福克-普朗克方程中,漂移变量相应地表述为漂移向量,扩散变量相应地表述为扩散矩阵,因为此时y表示空间位置向量;反之,当y为一维变量值时,A(y,t)和B(y,t)都称为一维变量。式(12)则可满足样本路径连续性的要求,因此福克-普朗克方程描述了一个具有连续样本路径的过程x(t)。
下面分析式(12)右边A(y,t),B(y,t)及其偏导数的具体表示形式。在条件(9)下,条件(10)可以写为

A(y,t)为随机位移的平均值与时间差的比值,因此A(y,t)应为溶质粒子在多孔介质中的平均流速,有

在条件(9)下,条件(11)可以写为

德·若斯林·德戎提出[8]弥散系数为

再由方差定义可得

对于微小的Δt,福克-普朗克方程的解仍具有完整的陡峭尖峰形状,因此与p的导数相比,A(y,t)和B(y,t)的导数及其时间效应忽略不计时,可得到一维理想对流弥散方程为

将式(14),(16)代入方程(17),有

在一些物理过程中,需要考虑A(y,t)的导数,忽略B(y,t)的导数和两者的时间效应,式(10)两端对x求偏导数得

可知,式(19)表示一部分颗粒由在t时刻从位置y对流弥散运动到位置x的概率密度为f(x,t+Δt;y,t),速度为(x-y)/Δt。假定这部分颗粒在流体流动方向上发生吸附,且岩心中各位置颗粒发生吸附的概率密度为常数λ,平均吸附速度为v,则有

将式(14),(16),(20)代入方程(21),有
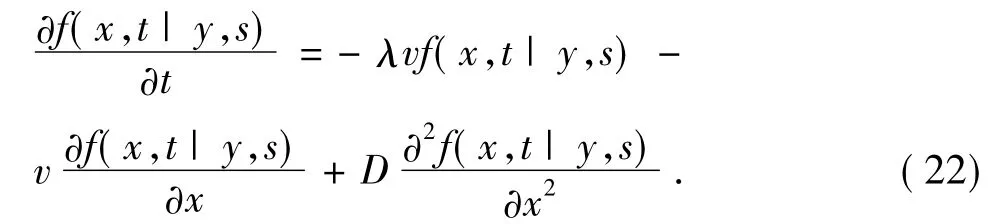
在一些物理过程中,考虑A(y,t),B(y,t)的导数而忽略两者的时间效应时,式(11)两端对x求偏导数得

式(12)的一阶导数展开有


将式(14),(16),(20),(23)代入式(24),有

因λ,D均为常数,则式(25)进一步展开得

将式(14),(16),(20),(23)代入式(26)得

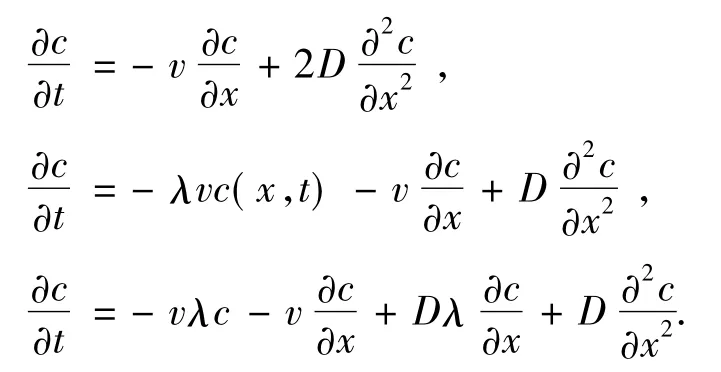
比较方程(6)到方程(7)和(8)的简化条件与漂移变量A(y,t)和扩散变量B(y,t)的导数关系,用下脚标D表示吸附的粒子,有下述关系:
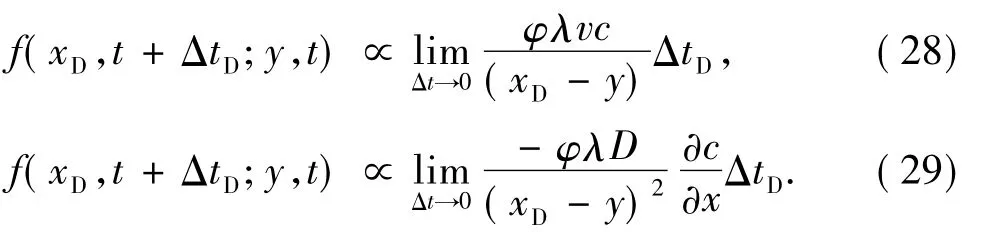
分析式(28)和(29)可知:①渗滤系数λ越大,发生吸附的颗粒概率密度越大,由于λ与颗粒-孔隙尺寸比有关,颗粒-孔隙尺寸比越大,λ越大,因此较细的颗粒容易通过多孔介质;②弥散系数D越大,颗粒浓度c越高,发生吸附的颗粒概率密度越大;③多孔介质的孔隙度φ越小,弥散颗粒样本路径(xD-y)越小,发生吸附的颗粒概率密度越大。即致密多孔介质孔隙度小,边界层流体较厚,颗粒发生吸附的运动路径较短,溶质颗粒更容易发生吸附。
3 结论
(1)同时考虑对流流量及弥散流量中粒子的俘获建立对流弥散数学模型,两者的作用效果使得颗粒在流动方向上的传递发生延滞。
(2)体积微元法与马尔科夫方法建立的对流弥散新模型及各简化条件下的模型具有完全一致的形式,一维情况下对流流量中颗粒的俘获项对应漂移变量的空间导数,弥散流量中颗粒的俘获项对应扩散变量的空间导数。
(3)渗滤系数越大,颗粒浓度越高,弥散率越大,发生吸附的颗粒概率密度越大;多孔介质孔隙度越小,弥散颗粒样本路径越小,发生吸附的颗粒概率密度越大。
[1]王健,姚恒申,罗平亚.化学驱过程中的扩散弥散机理研究[J].石油勘探与开发,2000,27(3):40-43.WANG Jian,YAO Heng-shen,LUO Ping-ya.The diffusion and dispersion mechanisms in chemical flooding process[J].Petroleum Exploitation and Development,2000,27(3):40-43.
[2]张富仓,康绍忠,潘英华.饱和-非饱和土壤中吸附性溶质水动力弥散实验研究[J].水利学报,2002,3:84-90.ZHANG Fu-cang,KANG Shao-zhong,PAN Ying-hua.Experimental study on hydrodynamic dispersion of adsorption solute in saturated-unsaturated soil[J].Journal of Hydraulic Engineering,2002,3:84-90.
[3]崔传智,栾志安.溶剂驱油中的扩散现象研究[J].水动力学研究与进展,1997,12(1):72-79.CUI Chuan-zhi,LUAN Zhi-an.The study of diffusion phenomenon in solvent displacement[J].Journal of Hydrodynamics,1997,12(1):72-79.
[4]张德生,常安定,沈冰,等.土壤中吸附性溶质运移对流-弥散模型的准解析解及其数值模拟[J].水动力学研究与进展,2005,20(2):226-232.ZHANG De-sheng,CHANG An-ding,SHEN Bing,et al.Quasi-analytical solution and numerical simulation for advection-dispersion model of adsorbed solute transport through soils under steady state flow[J].Journal of Hydrodynamics,2005,20(2):226-232.
[5]陈静,黄冠华,黄权中.一维均质与非均质土柱中溶质迁移的分数微分对流-弥散模拟[J].水科学进展,2006,17(3):299-304.CHEN Jing,HUANG Guan-hua,HUANG Quan-zhong.Simulation of one-dimensional solute transport in homogeneous and heterogeneous soils with scale-dependent fractional advection-dispersion equation[J].Advances in Water Scienc,2006,17(3):299-304.
[6]ALTOÉ F J E,BEDRIKOVETSKY P,SIQUEIRA A G,et al.Role of dispersion in injectivity impairment:mathematical and laboratory study[R].SPE 90083,2004.
[7]IWASAKI T.Some notes on sand filtration[J].J Amer Water Works Assoc,1937,29(10):1591-1597.
[8]葛家理.现代油藏渗流力学原理[M].北京:石油工业出版社,2001:282-291.
[9]王子亭,郎兆新.对流-弥散问题的随机过程方法[J].石油大学学报:自然科学版,1996,20(6):29-31.WANG Zi-ting,LANGZhao-xin.Statisticalprocess method for the convective dispersion problem[J].Journal of the University of Petroleum,China(Edition of Natural Science),1996,20(6):29-31.
[10]HERZIG J P,LECLERC D M,LEGOFF P,et al.Flow of suspensions through porous media-applications to deep filtration[J].Ind Eng Chem,1970,62(5):8-35.
[11]王美岚.可逆马尔可夫链的转移概率估计[J].石油大学学报:自然科学版,2003,27(5):133-136.WANG Mei-lan.Estimation of transition probability for reversible MARKOV chains[J].Journal of the University of Petroleum,China(Edition of Natural Science),2003,27(5):133-136.
(编辑 李志芬)
Finite volume modeling method for random process of dispersive flow in porous media
WANG Chang-jiang1,JIANG Han-qiao1,QIN Sheng-gao2,LI Jun-jian1
(1.College of Petroleum Engineering in China University of Petroleum,Beijing 102249,China;2.Petroleum Engineering College of Northeast Petroleum University,Daqing 163318,China)
A dispersion model with adsorption was derived by finite volume modeling method.It can be simplified to the HLL model and further to the ideal model under certain conditions,of which the physical meanings were analyzed also.Compared with the process of derivation by Markov method,the finite volume modeling method was developed based on statistical mechanism of random processes for the model construction and simplification conditions.In the two methods,the spatial derivative of the drift variable matches along with the particle adsorption item of the convective flux while the spatial derivative of the dispersive variable matches along with the particle adsorption item of the dispersive flux.The results indicate that the bigger the infiltration coefficient,the higher the particle concentration and the larger the dispersion ratio,then the greater the probability density of the particles to be adsorbed.The shorter the sample route of the dispersive particles,the greater the probability density of the particles to be adsorbed.
finite volume modeling method;convective dispersion equation;Markov method;particle retention
TE 357.46
A
10.3969/j.issn.1673-5005.2011.01.018
2010-03-10
国家科技重大专项课题(2008ZX05024-02-12);国家“863”重点基础研究发展规划项目(2007AA090701)
王长江(1980-),男(汉族),安徽安庆人,博士研究生,主要从事油气藏工程和渗流力学方面的研究。
1673-5005(2011)01-0093-05
