管翅式换热器流动和换热的低阶模型模拟

丁 鹏,陶文铨

(1.中国石油大学储运与建筑工程学院,山东青岛266555;2.西安交通大学能动学院,陕西西安710049)

管翅式换热器流动和换热的低阶模型模拟

丁 鹏1,陶文铨2

(1.中国石油大学储运与建筑工程学院,山东青岛266555;2.西安交通大学能动学院,陕西西安710049)

采用最佳正交分解技术(POD)建立管翅式换热器的低阶模型,通过数值模拟的方法得到管翅式换热器在雷诺数为100～2000时的流场和温度场。通过对系统样本实施最佳正交分解得到该物理问题的POD基函数和谱系数。POD基函数具有能量最优的特性,即在重构公式中使用较小的截断自由度可将原物理问题的解准确地表示出来,重构公式在非设计参数时的谱系数由线性插值的方法得到。研究结果表明,基于POD的低阶模型可以快速、准确地预测出管翅式换热器内的温度场和速度场,计算时间仅为S IMPLE算法的1/1200。

最佳正交分解;低阶模型;管翅式换热器;对流换热;数值模拟

管翅式换热器广泛应用于暖通空调、石油化工等行业。这类换热器的热阻主要在空气侧,因此强化空气侧换热是提高其综合性能的关键。对空气侧常用的强化措施主要是采用各种强化换热翅片(如波纹翅片、开缝翅片、百叶窗翅片等),这些翅片周期性改变主流方向,从而增强换热效果,但同时流动阻力也大大增加。随着节能要求的不断提高,高效低阻的空气侧结构的研究和优化势在必行。各种结构复杂的新型开缝翅片被开发,这些新型的开缝翅片含有很多开缝和不规则的突起,通过试验手段对各种翅片进行优化设计会花费较高的试验费用和加工成本,同时也难以捕捉其详细的流场信息和温度分布。近年来,数值模拟方法在石油化工等领域得到了广泛的应用[1-3],采用数值方法可以获得计算区域中每一点的流动和温度信息,从而可以进一步对管翅式换热器进行优化设计。对管翅式换热器进行三维的整场数值模拟,通常会使用百万量级的网格,会消耗大量的内存空间和计算时间。笔者采用最佳正交分解技术建立管翅式换热器的低阶模型,低阶模型可以在很短的时间内得到较为准确的结果。

1 POD的理论基础

最佳正交分解(proper orthogonal decomposition,

POD)是一种功能强大、效果显著的高效数据处理方法,它可以把高维的物理过程用最佳级数展开的形式进行低维的近似描述,它提供了一个能够准确描述高维数据的低维空间。POD在流动传热问题中的应用可见文献[4-7]。假设f(x,tn)为一物理场,

比如温度场、速度场等,其中参数tn为获得此物理场时的参数,f(x,tn)可以通过数值方法得到并称之为一个样本。POD的最终目的是将f(x,tn)表示为以下级数形式:

式中,α(tn)为谱系数;φ(x)为POD基函数;M为截断自由度。

求解POD基函数φ(x)的过程等同于求解以下积分特征值问题[8-9]:

式(3)仅能获得设计参数tn对应的αk(tn)值。对于非设计参数t,由于t对应的物理场f(x,t)为待求,所以无法通过式(3)求出αk(t)的值。本文中通过线性插值的方法求得非设计参数t对应的αk(t),

将描述谱系数α演化的方程称为低阶模型。

最后,非设计参数t对应的物理场f(x,t)可以用重构公式(1)方便地求出。此时在重构公式中采用的基函数φ(x)仍是由设计参数时的物理场求出的基函数。

2 样本收集

图1为管翅式换热器示意图。雷诺数Re的变化范围为100～2000。图1所示的阴影部分的网格数为152(x)×35(y)×16(z)。建立低阶模型的第一步是采集系统样本,应该遵循的原则是使样本尽可能多地含有原系统的动力学信息。采用S IMPLE算法[11-13]分别求解了21个Re时的速度场和温度场,并将其分别存储在样本矩阵中,这21个设计参数分别是Re1=100,Re2=300,Re2=500,…,Re21=2 000。可以看出这些样本对应的是换热器在整个层流范围内的流场和温度场。试算表明增加样本数量不能进一步提高低阶模型的精度,所以可认为采用21个样本即可获得与样本个数无关的解。

图1 管翅式换热器示意图Fig.1 Schematic diagram of tube-fin heat exchanger

3 结果分析

采用“快照”方法对采集到的速度和温度样本进行最佳正交分解,共可得到21组基函数和21个特征值。表1中给出了速度样本和温度样本的前5个ξ与η的计算值。观察可以发现两个样本的ξ值减小很快。由最佳正交分解的性质[9]知,通过POD获得的基函数具有“能量”最优(对于速度样本而言,“能量”具有严格的物理意义,代表动能;对于温度样本而言,可以理解为在式(1)中的贡献程度)和快速收敛的特性,即仅用前面几个基函数就可以通过式(1)重构出较为准确的结果,仅使用前3组基函数就可以捕捉到原系统99.98%以上的能量。图2中给出了前3组速度基函数的矢量图和前3组温度基函数的等值线分布图。由图2可以发现,排在前面的基函数代表物理场中大尺度的结构,而排在后面的基函数则含有越来越多的小尺度结构。

表1 计算得到的ξ与η值Table 1 Calculated value ofξandη%

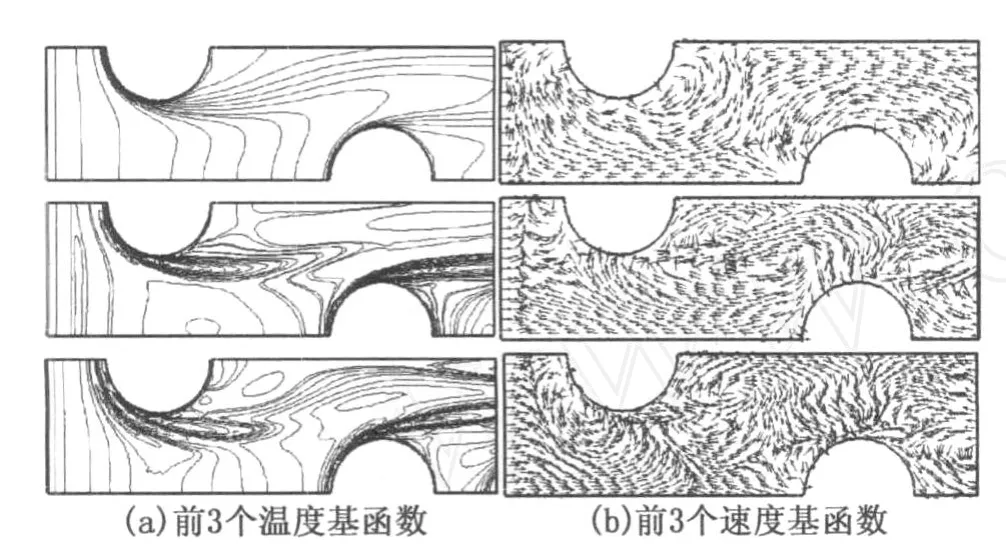
图2 由POD技术计算得到的基函数分布Fig.2 Basis functions obtained by POD technique

现定义相对误差E=‖f(x,t)-f(x,t)POD‖‖f(x,t)‖,其中‖·‖代表范数。相对误差E表示由低阶模型计算得到的物理场f(x,t)POD与数值解f(x,t)的相对偏差。

图3中给出了设计参数时的温度场和U速度分量的重构相对误差E。由图3(a)可以发现,相对误差E随着截断自由度M的增加而迅速减小,当M=6时,E的数值已经到了1%左右。与温度场相比,速度场需要较大的截断自由度M才能达到同一精度。

为了检验低阶模型在计算非设计参数时的准确度,采用低阶模型分别计算了3个非设计参数Re=386,1625和1915时的温度场和流场。这3个非设计参数对应的谱系数αk(t)由低阶模型(4)计算得到,最后利用重构公式(1)得到温度场和流场。图4中给出了非设计参数条件下的相对误差E与阶段自由度M的关系。由图4可以发现,在非设计参数条件下,低阶模型同样给出了比较准确的结果,并且误差E随着M的增加逐渐下降并趋于一个固定值。图5中给出了Re=1915时中心平面上的等温线分布。由图5可以发现,低阶模型的计算结果与数值解几乎相同。

图5 中心平面上的等温线分布Fig.5 Isotherm distribution of center plane

表2为S IMPLE算法与低阶模型所需计算时间对比。低阶模型的优势是非常明显的,要比S IMPLE算法快1200倍。低阶模型的计算时间并没有包括前期收集系统样本计算基函数的时间,这个阶段属于低阶模型的“训练”阶段。在实际的应用中,求得POD基函数后,低阶模型可以直接对其进行调用而不用再次求解。

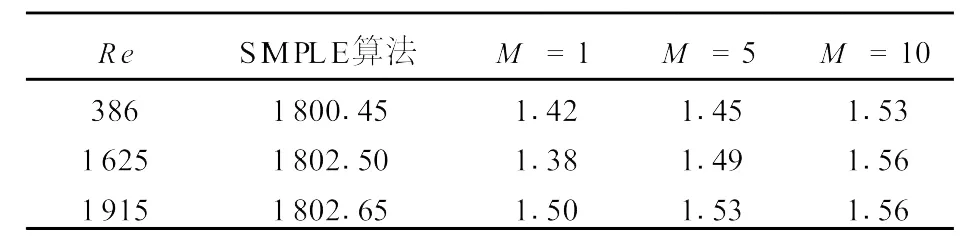
表2 S IM PLE算法与低阶模型所需计算时间对比Table 2 Comparison of computation t ime between S IM PLE and ROM methods

4 结束语

采用最佳正交分解(POD)技术建立了一管翅式换热器的低阶模型,非设计参数条件下重构公式中的谱系数采用线性插值的方法得到。与数值解对比,低阶模型在设计参数和非设计参数时均给出了相当准确的结果,并且在计算时间上有明显的优势。与S I M PLE算法相比,计算速度提高了1200多倍。

[1] 岳大力,吴胜和,程会明,等.基于三维储层构型模型的油藏数值模拟及剩余油分布模式[J].中国石油大学学报:自然科学版,2008,32(2):21-27.YUE Da-li,WU Sheng-he,CHENG Hui-ming,et al.Numerical reservoir simulation and remaining oil distribution patterns based on 3D reservoir architecture model[J].Journal of China University of Petroleum(Edition of Natural Science),2008,32(2):21-27.

[2] 金有海,姬广勤,曹晴云,等.旋风分离器排气管内气相流场的数值模拟[J].中国石油大学学报:自然科学版,2008,32(6):109-112.J IN You-hai,J I Guang-qin,CAO Qing-yun,et al.Numerical simulation of gas-phase flow field in vortex finder of cyclone separators[J].Journal of China University of Petroleum(Edition of Natural Science),2008,32(6):109-112.

[3] 高慧,周晓君.气液两相分层流动相界面迁移的数值模拟[J].中国石油大学学报:自然科学版,2009,33(1):68-73.GAO Hui,ZHOU Xiao-jun.Gas-liquid two-phase stratified flow[J].Journal of China University of Petroleum(Edition of Natural Science),2009,33(1):68-73.

[4] D ING P,WU XH,HE YL,et al.A fast and efficient method for predicting fluid flow and heat transfer problems[J].AS ME Journal of Heat Transfer,2008,130:1-17.

[5] D ING P,TAO WQ.An inverse analysis for the estimation of boundary heat flux in a circular pipe employing the proper orthogonal decomposition[J].Progress in Computational Fluid Dynamics,2009,9(3):231-246.

[6] SEMPEYA, INARD C,GH IAUS C,et al.Fast simulation of temperature distribution in air conditioned rooms by using proper orthogonal decomposition[J].Building and Environment,2009,44(2):280-289.

[7] L IBERGE E,HAMDOUN IA.Reduced order modelling method via proper orthogonal decomposition(POD)for flow around an oscillating cylinder[J].Journal of Fluids and Structures,2010,26(2):292-311.

[8] BERKOOZ G,HOLMES P,LUMLEY J L.The proper orthogonal decomposition in the analysis of turbulent flows[J].Annual Review Fluid Mechanic,1993,25:539-575.

[9] HOLMES P,LUMLEY J L,BERKOOZ G.Turbulence,coherent structures,dynamical systems and symmetry[M].U K,Cambridge:Cambridge University Press,1996.

[10] SIROV I CH L.Turbulence and the dynamics of coherent structure:PartⅡ,Ⅱ,Ⅲ[J].Q Appl Math,1987,XLV(3):561-571.

[11] PANTANKAR SV.Numerical fluid flow and heat transfer[M].New York:Academic Press,1981.

[12] 陶文铨.数值传热学[M].2版.西安:西安交通大学出版社,2001.

[13] PATANKA SV,SPALD ING DB.A calculation procedure for heat,mass and momentum transfer in three-dimensional parabolic flow[J].International Journal Heat Mass Transfer,1972,15:1787-1806.

(编辑 沈玉英)

Reduced order modeling of fluid flow and heat transfer in tube-fin heat exchanger

DING Peng1,TAO Wen-quan2

(1.College of Storage&Transportation and Architectural Engineering in China University of Petroleum,Qingdao266555,China;2.School of Energy and Power Engineering,Xi´an Jiaotong University,Xi´an710049,China)

The reduced order model(ROM)of a tube-fin heat exchanger was developed based on the proper orthogonal decomposition(POD)technique.The flow and temperature fields of a tube-fin heat exchanger were obtained from numerical simulation at different Reynolds number,which is 100-2 000.The best orthogonal decomposition method was used to the system sample to get POD basis functions and spectral coefficient.The POD basis function has the best characteristics of energy.In the reconstruction formula,a smaller cut freedom may be the solution of the original physical problem accurately.The spectral coefficient in non-design parameters was obtained by linear interpolation at the reconstruction formula.The results show that the reduced order model can predict the temperature and velocity field of the tube-fin heat exchanger quickly and accurately and the calculation time is 1200 times faster than that of S IMPLE algorithm.

proper orthogonal decomposition;reduced order model;tube-fin heat exchanger;convection heat transfer;numerical simulation

TK 124

A

10.3969/j.issn.1673-5005.2011.02.024

2010-09-22

国家自然科学基金青年基金项目(51006121)

丁鹏(1980-),男(汉族),山东曲阜人,讲师,博士,主要从事计算流体、传热反问题及油藏数值模拟方面的研究。

1673-5005(2011)02-0137-04