湍流弥散对轴心通风器油气分离过程的影响
2011-09-28徐让书宗庆贺刘立博王娟娟
徐让书,宗庆贺,刘立博,王娟娟
(沈阳航空航天大学动力与能源工程学院,沈阳 110136)
0 引言
美国F110等先进航空发动机的润滑系统大多采用轴心通风装置。这种结构在保证油腔内空气与大气相通的同时,还可以将油雾中的油滴分离出来,从而减少或取代传统的离心通风器,简化发动机结构,对提高其性能具有重要意义[1-2]。
轴心通风器内部流道结构比较复杂,并处于高温工作区,其内部流动的空气和滑油相互作用,形成复杂的气液两相流动[3]。在高速旋转流场中,离心分离是主要分离机理。然而,强烈的湍流具有较大的速度脉动,可以改变油滴颗粒的“正常”运动轨迹,造成颗粒的湍流弥散,对轴心通风器内分离过程的影响同样不可忽略。但是,由于光学测量受到空间的限制和流场试验十分耗时,进行详细的油滴轨迹跟踪试验研究难度很大。Glahn[4]等指出,对于颗粒运动分析需要采用数值计算与试验相结合的方法来进行。
本文对某轴心通风器试验装置进行CFD数值计算。使用RSM湍流模型模拟通风器内的复杂的带有强湍流的流动。在考虑湍流弥散对颗粒轨迹的影响时,采用随机追踪(Stochastic Tracking)模型;且采用壁面液膜模型(Wall FilmModel)模拟油滴碰壁后的运动形式。通过比较计算结果,讨论湍流弥散对轴心通风器分离过程的影响。
1 数学模型
在航空发动机轴心通风器中,油滴的体积分数约为8%~10%,属于稀相两相流[5,7]。这种形态的两相流动,采用Euler-Lagrangian方法描述较为合适。因此,在计算过程中使用DPM模型来模拟油滴的运动。
1.1 气相控制方程
(1)连续性方程
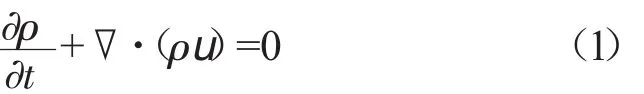
式中:ρ为空气密度;u为速度矢量。
(2)动量方程
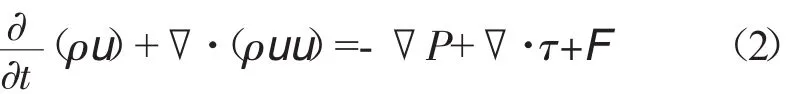
式中:P为静压;F为外部体积力矢量(考虑来自分散相作用力);τ为应力张量。
1.2 油滴相控制方程
轴心通风器内油滴的体积分数较小,可以忽略油滴间的相互作用。由于油相表面张力较大,所以假设油滴颗粒为球形,且不变形。油滴颗粒被看作惰性颗粒,即不考虑润滑油的蒸发。在Lagrangian参考系下,通过积分颗粒的运动方程计算其运动轨迹。忽略虚假质量力、压力梯度力、Magnus力、Basset力等作用。由颗粒的惯性与受力平衡,给出颗粒运动方程为
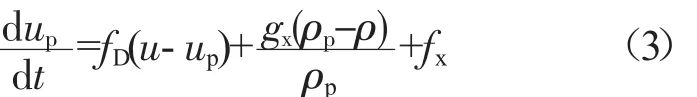
式中:up为颗粒速度;ρp为颗粒密度;fx为附加加速度项;fD(u-up)为单位颗粒质量受到的阻力。
1.3 分散相随机追踪模型
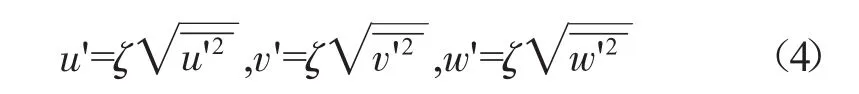
式中:u、v、w分别为速度分量;ζ为1个正态分布随机数。
1.4 壁面液膜模型
相关研究表明,在壁面温度不同时,液滴动量和入射角度不同,与壁面碰撞的相互作用可能产生油滴反弹、黏附、散布或飞溅等4种结果。对此,采用壁面液膜模型作为油滴碰壁的壁面边界条件,可以根据碰撞能量和壁面温度条件进行判断[6]。
碰撞能量
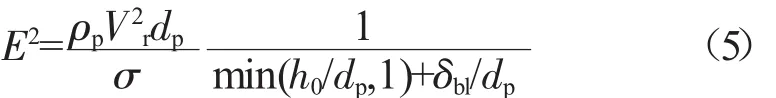
式中:Vr为液滴颗粒相对于壁面的速度;dp为油滴直径;σ为液体表面张力;h0为初始液膜厚度;δbl为边界层厚度。
2 计算域及网格划分
2.1 研究对象
以某型发动机轴心通风器为研究对象,其内部结构如图1所示。
在该试验器中,油气混合物从进气管进入试验器后,被高速旋转的转子轴带动而旋转,然后经转子轴上的径向孔进入轴心通风器。
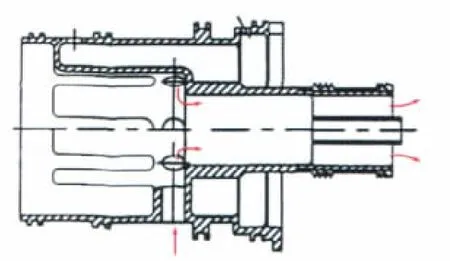
图1 某型发动机轴心通风器
2.2 计算域及网格划分
该模型计算域包括试验器、进气管、通风管以及通风器的内部流道。除转子轴和通风器是旋转部件外,包括试验器在内的其它部件均是固定部件。因而,随着通风器的转动,计算域是变化的。因此,采用滑动网格方法进行计算。用圆柱面将计算域分为固定网格区域和运动网格区域2部分,之间的滑动网格截面为非一致网格界面。设置动网格区域与通风器相同的旋转速度,则与旋转域相邻的旋转壁面(转子轴表面和通风器表面)相对于该区域的转速为0。
网格划分大部分采用6面体网格、部分区域如进气管与通风器的过渡区域以及环形腔等处的单元为4面体单元,关键的壁面附近采用边界层网格,保证壁面y+在合理的范围内,从而保证了较高的网格质量。网格总数约为160万的方案的求解结果具有网格的独立性。
考虑到采用整体模型计算时不易收敛和非常耗时,本文在确保计算结果不受影响的前提下,对计算域进行适当调整。调整后的计算域包括试验器内转子轴径向孔进口附近的环形空间、通风器的内部空间以及1段通风管。该区域的流动具有以近似60°为周期的旋转周期性,因此,局部计算域仅需取其1/6扇区。同样划分了几种疏密度的网格,局部计算域网格单元总数约为70万时具有解的独立性。
3 边界条件及求解
3.1 边界条件
整体计算模型与局部计算模型采用相同的参考压力,即标准大气压力。
整体计算模型根据试验条件进行设定:模型进口采用压力进口边界条件,出口采用压力出口边界条件。试验器出口为大气条件,试验器进、出口压力差Δp为8 kPa。则计算模型进口总压和出口静压分别为8000 Pa和0 Pa,流动方向均垂直于进、出口面。计算模型进口总温为378 K。颗粒相按对数Rosin-Rammler分布函数定义油滴颗粒群尺寸,分布指数为3.5,质量流量率为8.8×10-5kg/s。通风器试验器以及其进气管壁面为固定壁面。转子轴和通风器的所有表面为运动壁面,运动方式定义为与相邻单元区域相对旋转速度为0,所有壁面剪切条件均为无滑移,颗粒碰壁处理采用壁面液膜模型作为壁面边界。
局部计算模型:取所截的整体计算模型内径向孔进口附近的环形空间区域的剖面函数,作为局部计算域的进口边界条件。其采样所得到的颗粒分布作为喷射边界条件。周向的截面均设置为周期性边界条件。出口和壁面的边界条件均与整体模型运动部分的相同。
3.2 求解
整体计算模型计算主要是为获得局部计算模型的边界条件。考虑到局部计算模型进口面附近的流动主要是由周期性结构引起的周期性非定常流动,时间步长取通风器旋转1周时间的1/150,即主要非定常流动周期的1/25。因此,通风器转速为2000、4000r/min时,整体和局部计算模型的计算时间步长分别为2×10-4、1×10-4s。
4 计算结果及分析
计算结果表明,轴心通风器内湍流强度平均约为13%,属于较强烈的湍流流场。这样,流体微团的随机脉动速度会带动惯性较小的小尺寸颗粒产生相对于平均流的随机脉动运动,进而加强颗粒的迁移[8]。本文通过是否采用随机追踪模型的方法,模拟忽略和考虑湍流弥散的2种情况。根据分离效率的差异,判断在湍流流场分布不变的条件下,湍流的脉动速度对分离过程的影响。
4.1 分离效率
分离效率是评价通风器油气分离性能的重要指标,表征通风器从流体中收集油滴颗粒的能力。通过采集一定时间内逃离进口和通过出口的油滴颗粒。可得分离效率为

式中:mp,outlet为通过局部计算模型出口面被采样的颗粒质量流量,既未分离颗粒质量流量;minj为喷射文件中全部颗粒包的质量流量;mp,inlet为通过局部计算模型进口面被采样的颗粒质量流量。
计算分段分离效率可以分析通风器各段对油气分离的贡献。与计算总分离效率的方法类似,分段分离效率表示为
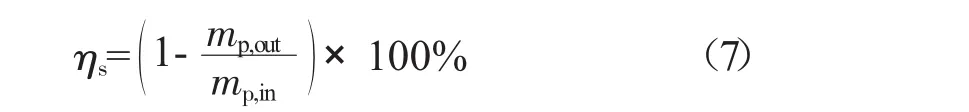
式中:mp,out为通过某段出口面被采样的颗粒质量流量,即未分离颗粒质量流量;mp,in为通过某段进口面被采样的颗粒质量流量。
整体分离效率见表1。其结果表明,在使用随机轨迹追踪模型时,油气分离效率的计算结果与试验测量值符合得很好。
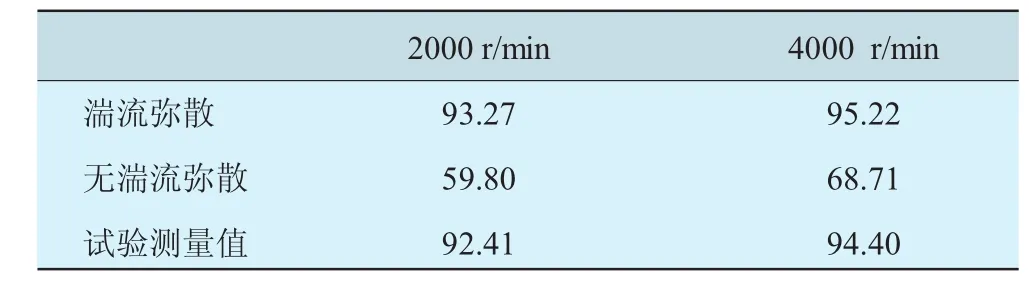
表1 有无湍流弥散情况下计算所得整体分离效率 %
4.2 分离机理
各段分离效率对比见表2、3。从表中可见,环形腔和通风管的油气分离过程是轴心通风器的主要分离阶段。在环形腔中,径向距离较短,由第1级径向孔流入环形腔的空气首先冲向通风器外表面,在环形腔内折回后流入通风孔。在此过程中,细小的油滴颗粒随空气一起运动,而粗大的油滴颗粒具有较大的惯性,在空气折回流动时会脱离流线,与壁面发生碰撞,发生惯性分离。
在通风管中,由通风孔进入通风器内腔的混合气,经低压转子轴高速旋转的带动形成强旋气流,其主要的分离机理是离心分离。
对比2000 r/min和4000 r/min 2种工况,在环形腔中,在高转速工况条件下油滴运动速度较大,动能较大,由于是惯性分离,所以油滴碰到壁面后更容易发生反弹或飞溅,而非黏附,这不利于油滴的分离。但在通风管中,转速越大,离心力就越大,更有利于油滴分离出来,因此,在通风管中分离效率与转速成正相关,而环形腔则相反。
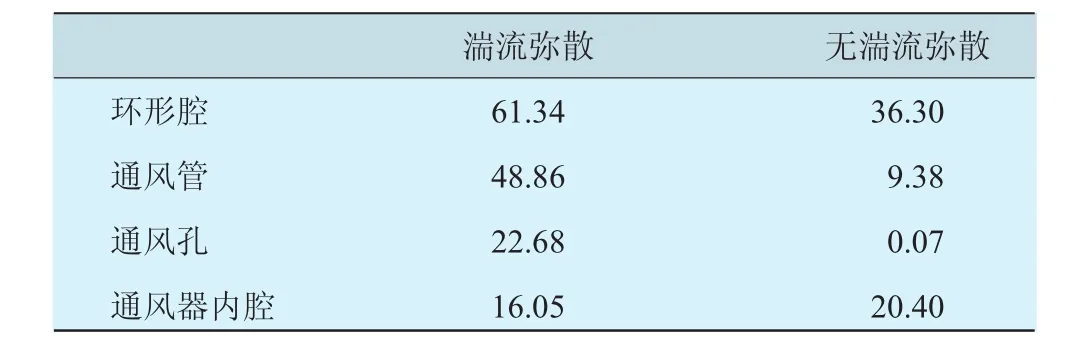
表2 2000 r/min工况下各分段分离率 %
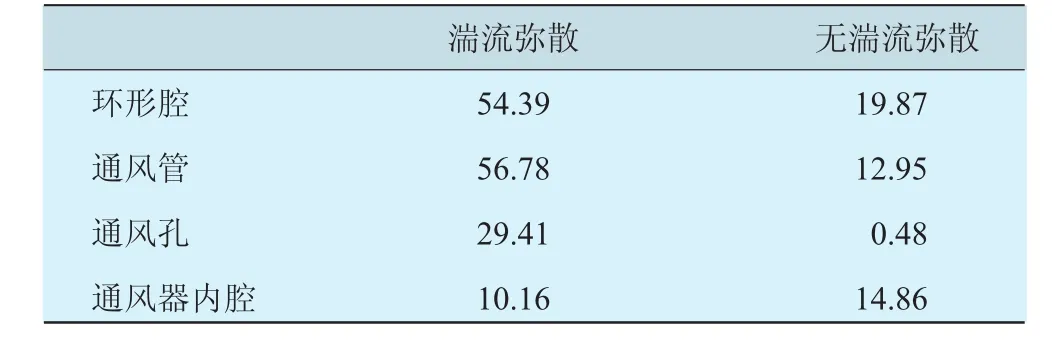
表3 4000 r/min工况下各分段分离效率 %
4.3 湍流弥散的影响
从表1示出的整体分离效率上看,忽略湍流弥散的分离效率大约为正常分离效率的2/3,转速增大,其比值减小到约3/4。由此可以看出见,湍流弥散在轴心通风器的分离过程中起着非常重要的作用。
在环腔位置,分离效率可以在湍流弥散的作用下提高20%以上。而在离心力起主要作用的的通风管中,湍流弥散的影响更为明显,2种情况下的分离效率相差数倍。通风管壁面上的油膜分布如图2所示。如果没有湍流的脉动作用,油滴基本全部跟随旋转气流的运动轨迹,撞击到壁面的油滴所形成的油膜大多分布在气流经过的位置,而湍流脉动引起的颗粒弥散改变了油滴的“正常”运动轨迹,可以使油膜在壁面上的分布更为均匀,分离出的油滴也更多。
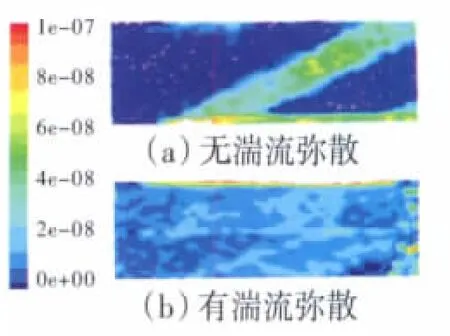
图2 通风管壁面油膜分布
对于起着2级分离作用的轴心通风器,特别是对处于分离最后阶段的通风管而言,其中小直径的油滴占更多更大比例,小直径油滴相对于比大直径油滴更容易受到湍流脉动的影响。通风管中沿径向的向心加速度分布趋势是先增大,后减小,如图3所示,在半径3/11处达到最大值。在忽略湍流脉动作用的情况下,在向心加速度最大的位置,几乎没有油滴的存在,如图4(a)所示。小尺寸油滴质量较小,在其高度集中的区域,其向心加速度同样也很低小。因此,小油滴所受到的离心力不足以使其运动到壁面完成分离,大量的小油滴在径向3/4位置大量的小油滴均随空气排出。可是在湍流弥散作用下,如图4(b)所示,无论是径向还是轴向的湍流脉动,都会使小油滴的分布更加均匀,在向心加速度很高大的位置,可以使质量小的油滴获得相对较大的向心力,有利于小油滴的分离。
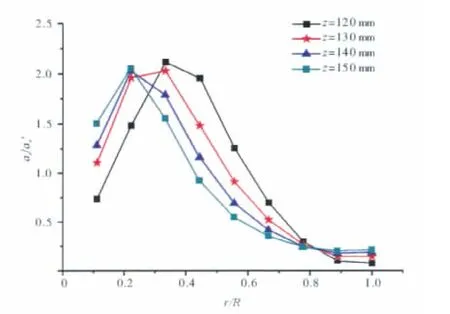
图3 通风管中径向向心加速度分布
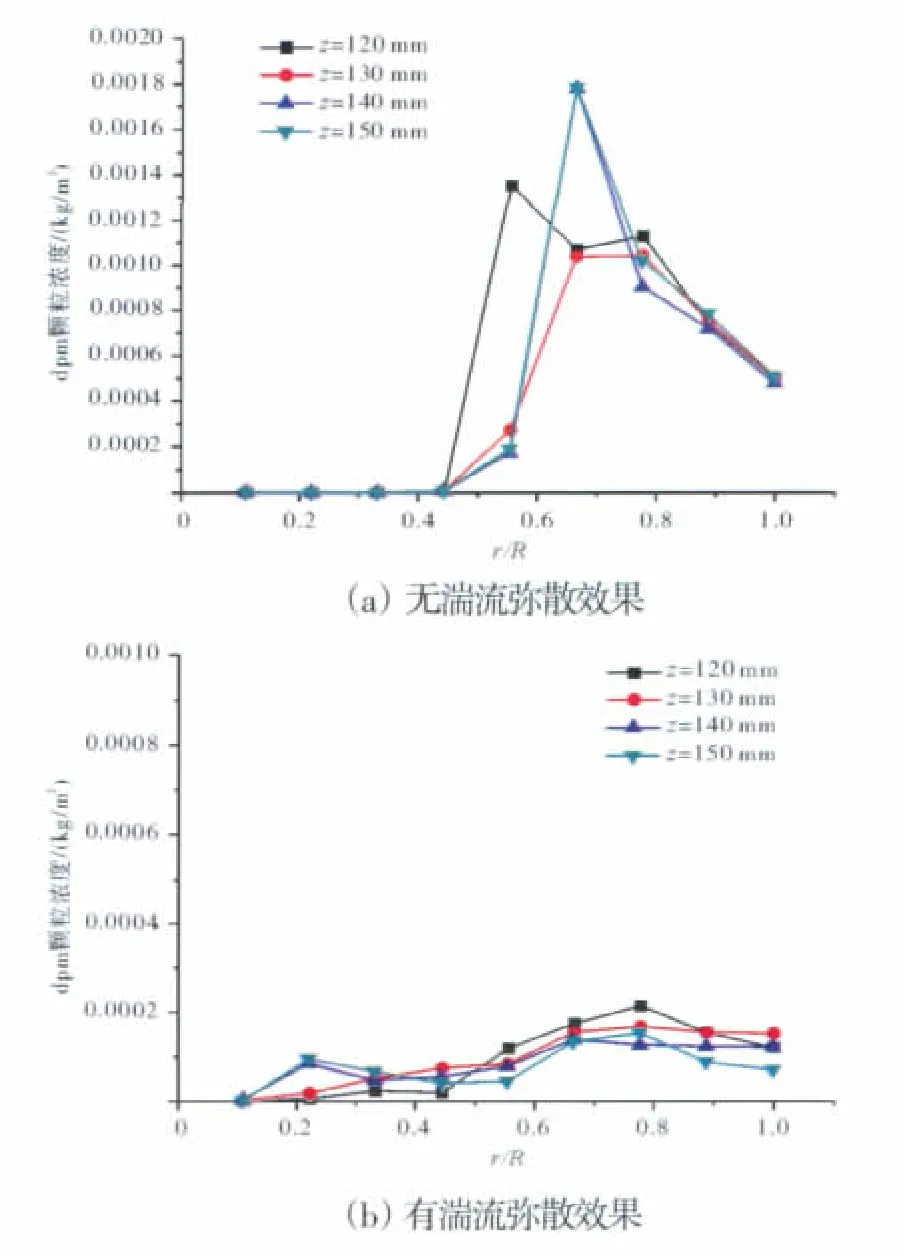
图4 通风管中径向油滴浓度分布
此外,湍流弥散使油滴在流出管道的过程中运动轨迹曲折,延长了其运动到通风器出口的时间,这样反复复杂的运动也可以增大分离油滴的几率。所以,在通风管中,湍流脉动引起的颗粒弥散在空间和时间上均对分离过程起到了重要作用。
在通风孔位置,平均气流方向与壁面基本平行,几乎没有撞壁运动,如图5所示。但是,在湍流沿孔的径向脉动作用下,油滴颗粒仍可以向壁面运动,令此处具备了一定的分离能力。
但是,在通风器内腔位置,湍流弥散的作用反而减弱了此处的分离效果。在通风器内腔处于通风孔和通风管的交界处,即油气混合气进入轴心通风管的入口处,运动情况复杂,存在很多涡流。湍流脉动令油滴颗粒摆脱了拟序涡结构,使其未能很好地分离就进入了后端的通风管。不过从数值上看,该位置分离效率较低,在整体分离过程中所起到的作用并不大,并且湍流弥散所引起的反作用更小,可以忽略不计。从结构优化的角度考虑,可以将径向通风孔与轴心相交的位置适当前移,这样,既可以减小通风器内腔空间,削弱湍流脉动不良影响,还可以增加分离能力更强的通风管的作用范围。
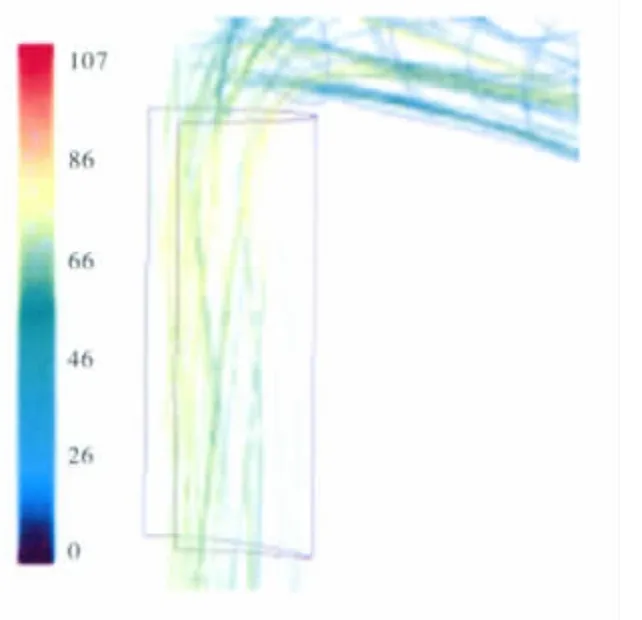
图5 通风孔内气相流线
4.4 湍流强度
湍流强度是反映湍流脉动速度相对于时均速度的强弱程度。通风管中不同轴向位置的湍流强度沿径向分布如图6所示。通风器内腔位置湍流强度最大,说明此处湍流最为剧烈,是后端通风管内湍流脉动的主要来源。在径向上靠近壁面位置,湍流强度有明显减小趋势,这可以减少由于较大的湍流脉动所引起向壁面运动的油滴偏离轨迹的概率和避免壁面上油膜的2次飞溅[9]。
5 结论
(1)在轴心通风器中,环形腔和通风管起主要分离作用。其中环形腔主要分离机理为惯性分离,通风管主要分离机理为离心分离。
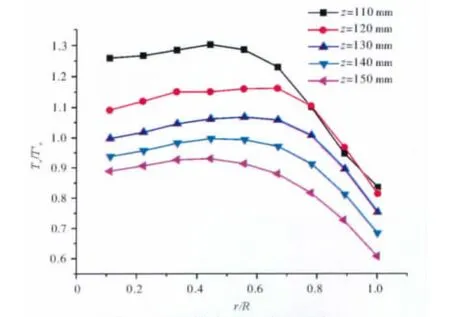
图6 通风管内径向湍流强度
(2)湍流脉动可以提高轴心通风器的油气分离能力。在通风孔和通风管中,湍流弥散作用最为明显,环形腔次之,只有在通风器内腔湍流弥散对分离有反作用,但影响甚小,可以忽略不计。
(3)通风管内径向的湍流强度分布有利于油滴分离,并避免油膜2次飞溅。
[1]航空发动机设计手册总编委会.航空发动机设计手册:传动及润滑系统:第12册 [M].北京:航空工业出版社,2002:507-508.
[2]马玫.航空发动机轴心通风系统的结构演变及分析[J].燃气涡轮试验与研究,1994(4):23-30.
[3]马玫,赵炜.航空发动机轴心通风器油气分离技术研究及油滴运行轨迹跟踪[J].航空发动机,1997(2):13-16.
[4]Glahn A,Kurreck M,Willmann M,et al.Feasibility study on oil droplet flow investigations inside aeroengine bearing chambers-PDPA techniques in combination with numerical approaches[J].Journal of Engineering for Gas Turbines and Power,1996,118(4):749-755.
[5]车得福,李会雄.多相流及其应用 [M].西安:西安交通大学出版社,2007:516-520.
[6]Farrall M,Hibberd S,Simmons K.The effect of initial injection conditions on the oil droplet motion in a simplified bearing chamber[J].Journal of Engineering for Gas Turbines and Power,2008,130(1):1-7.
[7]周华,夏南.油气分离器内气液两相流的数值模拟[J].计算力学学报,2006,23(6):766-771.
[8]王兵,张会强,王希麟,等.湍流分离流动中的颗粒弥散机制[J].清华大学学报,2003,28(5):1507-1510.
[9]苏亚欣,岑可法,骆仲泱.方形旋风分离器内气固两相流湍流特性的研究[J].热能动力工程,2002,17(98):147-150.
