稀土离子4fn-15d组态的配位场理论*

范英芳 李彩云

(1山西大学分子科学研究所 山西太原 030006; 2武装警察学院基础部 河北廊坊 065000)

稀土离子在不同基质中产生的4fn-15d→4fn强跃迁可发射相干真空紫外光(VUV:λ<200nm,E>50000cm-1)或紫外光[1]，如LiYF4:Ce3+在325nm产生激光[2]；掺杂稀土离子的荧光材料可作为高量子产率的磷光体，应用于等离子体显示屏、汞灯管、快速闪烁器和光波通讯。第一个固态VUV激光是基于LaF3:Nd3+掺杂晶体中Nd3+离子的f-d发射[3]；Ce3+离子的荧光特性在闪光晶体中的运用被广泛研究[4]，而且因为成功制备掺杂Ce3+的激光材料，使得镧系离子4fn→4fn-15d(f-d)组态间的跃迁光谱引起人们的研究兴趣[5]。关于4fn-15d组态的理论研究因实验数据不足而受到很大限制，目前仅有少量的文献报道[6-7]，其拟合计算主要运用配位场理论模型，能级拟合涉及以下几个方面：4f组态的库仑作用、旋轨耦合和晶体场作用；5d组态的晶体场作用、旋轨耦合以及4f与5d电子的库仑作用。本文在这方面做了一些探索性研究，以4f15d1组态为例，运用配位场理论方法得到了4fn-15d组态的谱项和支谱项，探讨了波函数的推导及其配位场能级的计算方法。

1 4fn-15d组态的谱项和谱项波函数

1.1 谱项的推求

在给定的电子组态下，S、L有确定值的状态的全体称为一个谱项，用2S+1L表示。推求谱项有两种方法。

1) 逐级消去法。具体步骤如下：

① 求出组态所属全部微观状态的ML、MS值，并列表分类。

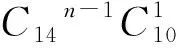
例如，对于4f15d1组态，ml1=±3,±2,±1,0；ml2=±2,±1,0。所以最大ML=5，最小ML=-5，全部微观状态的ML值有±5,±4,±3,±2,±1,0；而ms=+1/2或-1/2，故4f15d1组态的最大MS=1，最小MS=-1，全部微观状态的MS值有1,0,-1。据此，我们将4f15d1组态的微观状态按ML、MS值列入表1(只写出正值部分)。

② 从具有最大ML、MS值的微观状态开始，确定L及S值，决定其所属谱项。

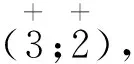
③ 从余下的微观状态中找出最大ML、MS值，确定其所属谱项。

除去属于3H谱项的所有微观状态后，具有最大ML、MS值是ML=5、MS=0，属1H谱项，它共有11个微观状态：ML=±5,±4,±3,±2,±1,0；MS=0。同样从表1中消去这11个微观状态。

④ 重复③步操作，直到找出该组态的所有谱项。

4f15d1组态共有10个谱项：3H,3G,3F,3D,3P,1H,1G,1F,1D,1P。

表1 4f15d1组态的微观状态*

*表中标记略去了φ、n、l，且第一个电子为4f电子。

2) 先组合4fn-1和5d组态的谱项，再得到组态4fn-15d的谱项。

4f1组态的谱项是2F，5d1组态的谱项是2D，将2F与2D两谱项耦合可得到4f15d1组态的谱项，其总轨道角动量量子数L=|L1-L2|,……,|L1+L2|，即L=5，4，3，2，1；总自旋角动量量子数S=|S1-S2|,……,|S1+S2|，即S=1，0。因此，4f15d1组态的谱项为3H,3G,3F,3D,3P,1H,1G,1F,1D,1P，这与上面推导的结果相同。由于4fn组态的谱项已经全部得到，所以用这种方法可以很方便地得到所有4fn-15d组态的全部谱项。

1.2 谱项波函数的推求

2 4fn-15d组态的支谱项及其波函数

2.1 支谱项的推求

4fn-15d组态的各谱项在旋轨耦合作用下简并度降低，分裂成一系列J-支谱项(2S+1LJ)，J的取值范围是|L-S|≤J≤|L+S|，简并度为(2J+1)，用支谱项波函数(|2S+1LJ,MJ〉)来表示，其中MJ=±J,±(J-1),…,±1,0。

例如，对于4f15d1组态的3H谱项，在旋轨耦合作用下可分裂成3个支谱项：3H6、3H5和3H4，它们的简并度分别为13、11和9。

2.2 支谱项波函数的推求

支谱项波函数由谱项波函数线性组合而成，即：

表2 4f15d1组态的MJ表

3 4fn-15d组态在S4对称场中的能量算符

在中心场近似下，稀土离子未充满壳层中N个电子运动的哈密顿算符为：

(1)

(2)

若将配体看作点电荷，则配体场参数Ak,m如下：

(3)

式中用到的球谐函数Yk,q的表达式参见文献[8]。

4 4fn-15d组态的能级能量

4.1 谱项能量

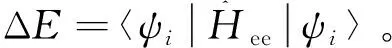
(4)

其中，

U(ai;aj)=I(ni,li;nj,lj)δli,ljδmli,mljδmsi,msj

(5)

Rk(ni,li;nj,lj;np,lp;nq,lq)

(6)

(7)

所以，

(8)

对于fd组态，k=1,3,5，Fk是由f,d组态共同决定的参数，有关它的具体数据迄今为止还没有看到，所以不能得到确切的能级分裂值。

4.2 支谱项能量

支谱项能量可由支谱项波函数的能量矩阵元求得，即：

(9)

(10)

(11)

采用相似的方法可得4f15d1组态其他支谱项的相对能量。由此可见，4fn-15d组态的相对支谱项能量值是由f和d轨道的旋轨耦合常数共同决定的。

4.3 配位场微扰能级的能量

5 S4对称场中的光谱跃迁选律

在S4点群对称场作用下，不可约表示基函数可以按照点群链关系SO(3)⊃O⊃D2d⊃S4组合得到，具体方法可参阅文献[9]。

在S4点群对称场中，uz属于B表示，Rz属于A表示，(ux,uy)、(Rx,Ry)属于E表示，根据直积关系可得到S4点群的电、磁偶极跃迁选律，如表3、表4所示。

表3 S4点群的电、磁偶极跃迁选律

表点群的电磁偶极跃迁选律

6 小结

到目前为止，由于缺乏Fk参数，通过理论计算还不能得到各谱项和支谱项的能量，因而也不可能通过计算得到各斯塔克能级的能量。另一方面，由于实验条件的限制，没有得到稀土离子4fn-15d组态的光谱精细结构，也就是说，没有足够的有关4fn-15d组态各斯塔克能级的实验光谱数据，所以也不可能通过与实验光谱拟合求得各斯塔克能级的能量。本文中虽然不能运用理论作定量的计算，但可以从理论上对实验光谱作一些定性的讨论。三价镧系离子的线状发射光谱主要是由电偶极跃迁引起，而磁偶极跃迁常影响谱线的强度。对于自由离子，4fn-15d组态的跃迁选律服从[10]：ΔS=0,Δl=±1,ΔL=0,±1,ΔJ=0,±1,(J=0→J=0禁阻),ΔL=ΔJ。但在配体场作用下，自由离子光谱选律失效，而跃迁选律应严格服从群论选律。

[1] Nicolas S,Laroche M.JPhysCondensMatter,1999,11:7937

[2] Ehrlich D J,Moulton P F,Osgood R M.OptLett,1979,4:184

[3] Waynant R W,Klein P H.ApplPhysLett,1985,46:14

[4] Van Eijk C W E.ProcSPIE，1996,2706:158

[5] Stephana M,Zachaub M,Grötinga M,etal.JournalofLuminescence,2005,114:255

[6] Dorenbos P.JournalofAlloysandCompounds,2002,341:156

[7] Duan C K,Reid M F.JournalofSolidStateChemistry,2003,171:299

[8] 冯星洪，曾成.化学通报，1984(1):15

[9] Fan Y F,Pan D F,Yang P.ScienceinChina,1997,B40(4):389

[10] Kollia Z,Sarantopoulou E,Cefalas A C,etal.OpticsComm,1998,149:386