关于导函数连续的条件分析

王雪琴

(渭南师范学院数学与信息科学系，陕西渭南714000)

关于导函数连续的条件分析

王雪琴

(渭南师范学院数学与信息科学系，陕西渭南714000)

通过对导函数特性的分析，得到了导函数连续的几个充分条件，为继续研究分段函数的连续性及后续的积分学提供了理论依据.

导函数连续性;一致可微;凹凸性;充分条件

1 预备知识

定义［4］设f(x)在区间I上有定义，若对时，有

则称f(x)在区间I上一致可微.

引理1［1］若函数f(x)在U(x0)内连续，在U0(x0)内可导，且极限存在，则f'(x)在x0点连续.

该引理是导函数的连续性定理，说明导函数极限存在就连续，即不存在第一类间断点.它与一般函数不同，这是导函数的一大特性.

引理2［5］若函数f(x)在开区间(a，b)内可导，且f'(x)在(a，b)单调，则f'(x)在(a，b)内连续.

该引理说明导函数如果单调就连续，但对一般函数而言，需要满足单调有界定理才能有极限，所以谈不上连续.它又体现了导函数的特性.

引理3［3］若函数f(x)在开区间(a，b)内可导，f(x)为凹(凸)函数当且仅当f'(x)为减(增)函数.

2 结论及证明

结论1 若函数f(x)在开区间(a，b)内可导，且f(x)为凹(凸)函数，则f'(x)在(a，b)内连续.

证明:由引理3及引理2可证得.

说明:若x0为f'(x)的间断点，则必是第一类间断点:即凹(凸)函数不存在第二类间断点.

结论2 若f(x)在区间I上一致可微，则f'(x)在区间I上连续.

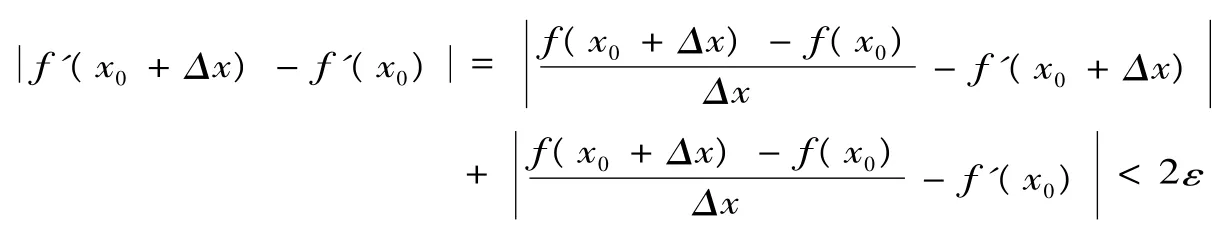
数学分析研究的对象是函数，导函数是函数中极其特殊的一类函数，而导函数的特性是数学理论与数学教学中值得探讨的一个课题，它对丰富数学的内容，培养学生数学思维的能力具有重要的意义.参考文献［1］、［2］、［3］中给出了导函数的连续性及介值性定理.本文在此基础上继续研究导函数连续的充分条件，得出几个重要结论.

由连续的定义知f'(x)在x0连续.由于x0的任意性，所以f'(x)在区间I上连续.

说明:可微是局部性，一致可微是整体性.一般情况下f(x)的导函数f'(x)不一定连续，但在一致可微的情况下导函数一定连续.

结论3 若f(x)满足f″(x0)存在.令，则g'(x)在x0连续.

证明:f(x)在x0的泰勒公式为

由引理1知g'(x)在x0连续.

说明:该函数是一个构造性函数.它与导函数的概念密切相关，它同样具有导函数连续性的特性.为研究导函数分段点的连续性及泰勒公式的延拓提供了理论依据.

3 结束语

从以上的分析研究可以看出，导函数是极其特殊的函数，它具有介值性但不要求其连续;具有连续性只要求有极限、单调或为凹凸函数.在此基础上，还可以继续研究导函数的其他特性及其这些结论的具体应用，为后续课程的学习及研讨奠定良好的理论基础.

［1］华东师范大学数学系.数学分析(第三版)［M］.北京:高等教育出版社，2003.

［2］谢惠民.数学分析习题课讲义(上册)［M］.北京:高等教育出版社，2003.

［3］刘玉琏.数学分析习讲义学习指导书(上册)［M］.北京:高等教育出版社，1990.

［4］裴礼文.数学分析中的典型问题与方法［M］.北京:高等教育出版社，2002.

［5］钱吉林.数学分析题解精粹［M］.武汉:崇文书局，2003.

［责任编辑 舒尚奇］

Abstract:The certain sufficient conditions of the continuity of derivative functions are obtained by the analysis of the characteristics of derivative functions，which offers a theoretical rationale for further study of the continuity of sub-function and the integral calculus.

Key words:continuity of derivative functions;consistent differentiability;convexity-concavity;sufficient conditions

The Analysis of Conditions of the Continuity of Derivative Functions

WANG Xue-qin
(Department of Mathematics and information Science，Weinan Teachers University，Weinan 714000，China)

O172

A

1009—5128(2011)02—0036—02

2010—10—26

王雪琴(1962—)，女，陕西大荔人，渭南师范学院数学与信息科学系副教授.