基于扩散滤波的多尺度三维变分研究

李冬，王喜冬,2，张学峰,2，吴新荣,2，李威，韩桂军

（1.国家海洋局海洋环境信息保障技术重点实验室 国家海洋信息中心， 天津 300171；2.中国科学院南海海洋研究所LED重点实验室，广东 广州 510301）

基于扩散滤波的多尺度三维变分研究

李冬1，王喜冬1,2，张学峰1,2，吴新荣1,2，李威1，韩桂军1

（1.国家海洋局海洋环境信息保障技术重点实验室 国家海洋信息中心， 天津 300171；2.中国科学院南海海洋研究所LED重点实验室，广东 广州 510301）

将扩散方程引入三维变分分析，揭示了传统 3D-VAR不能有效提取多尺度观测信息的根本原因，即观测导致的目标函数梯度在空间的不连续分布。将扩散滤波融入基于梯度的最优化算法，发展了基于扩散滤波的多尺度3D-VAR。海表面温度数据同化试验结果表明，新方法可从长波至短波有效地提取多尺度的观测信息。

三维变分；数据同化；各向异性；递归滤波；扩散方程

Abstract: The diffusion equation is introduced into 3D-VAR analysis in this paper.As it reveals, the root cause of the inefficiency of the traditional 3D-VAR scheme in extracting multi-scale information resolved by observations lies in the discontinuous distribution of gradient of the cost function caused by the inhomogeneous distribution of observations.A multi-scale 3D-VAR scheme is developed by incorporating diffusion filtering into gradient-based minimization algorithm.The new scheme is applied to a two-dimensional idealized SST assimilation experiment with real AVHRR SST observations, which shows a superior performance and the multi-scale observational information, and from longer to shorter wavelengths, such observational informationcan be extracted successively by this scheme.

Keywords: 3D-VAR; data assimilation; anisotropic; recursive filter; diffusion equation

1 引 言

气象、海洋三维变分数据同化（3D-VAR）通常可归结为如下目标函数的最小化问题（Lorenc 1986; Couriter 1997）

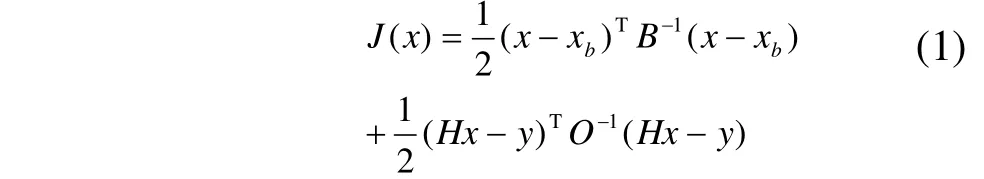
在递归滤波3D-VAR中，递归滤波的实质其实是高斯滤波，用以对背景误差协方差矩阵的作用进行模拟。由于高斯滤波最早来源于热扩散方程的求解，本文将从扩散滤波的角度认识3D-VAR，由此分析3D-VAR不能有效提取多尺度观测信息的根本原因，并将扩散滤波融入基于梯度的最优化算法，发展基于扩散滤波的多尺度3D-VAR。

文章第二部分简单介绍递归滤波3D-VAR；第三部分引入扩散方程，从扩散滤波的角度认识3D-VAR，并分析其不能有效提取多尺度观测信息的原因；第四部分提出基于扩散滤波的多尺度3D-VAR；第五部分将多尺度3D-VAR用于海表面温度（SST）同化试验，第六部分给出本文结论。

2 递归滤波3D-VAR简介

3D-VAR中的背景场误差协方差矩阵通常采用高斯函数进行描述，例如，对二维情形的各项同性的背景误差相关，B可表达为（Daley, R.,1991）:

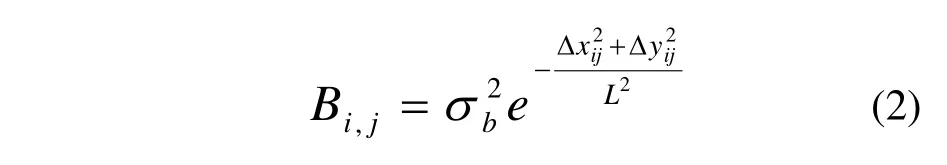
为了避免B的求逆及相关运算带来的巨大的内存与计算开销，并加快3D-VAR中优化算法的收敛速度，定义新的控制变量（Lorenc 1988; Derber 和Rosati 1989）：

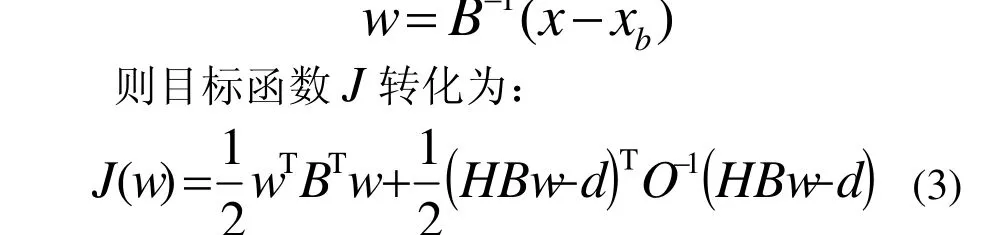
考虑到BT=B, (3) 可改写为：

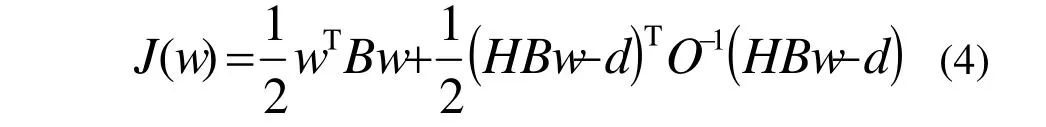
式中：α为滤波参数，决定了低通滤波器的带宽。α越大，带宽越窄，只有低频（长波）信息可以通过；α越小，带宽越宽，使得较高频率（短波）的信息也可通过。理论上可以证明，当 ，u为无限长序列，时，上述递归滤波器可逼近于一个一维的各向同性高斯滤波器。对高维情形，由各向同性高斯滤波的可分离性，可转化为多个一维递归滤波，例如，对二维情形，可以先对每一行进行滤波，再对每一列滤波。

递归滤波法，不需显式地构造B矩阵，而是通过选取滤波参数间接的反映B的信息，可显著减少因B矩阵的存储和相关运算带来的内存和计算开销。但在实际应用中，递归滤波方法最大的困难在于滤波参数的选取。以各向同性递归滤波为例，若选取的滤波参数α过大，则同化结果过于平滑，无法提取观测的短波信息；相反，若α过小，又不能准确地提取长波信息，于是短波信息也不可能很好的提取。

3 从扩散滤波的角度认识和分析3D-VAR

递归滤波3D-VAR中，递归滤波的实质是高斯滤波。由于高斯滤波最早即来源于扩散方程的求解，下面我们基于扩散方程，对传统3D-VAR进行分析，以探寻传统3D-VAR难以提取多尺度观测信息的根本原因。

3.1 3D-VAR中引入扩散滤波

高斯滤波可以通过求解扩散方程实现。考虑如下一维扩散方程的柯西问题：

以看出，扩散系数a和积分时间t决定了滤波器的频窗宽度（为4σ），也即代表了尺度。a越大，扩散越快，滤波越强，结果越平滑，得到的是低频信息；同理，积分时间t越长，结果也越平滑。显然，在积分时间固定的情形下，滤波的强弱仅取决于扩散系数的大小。另外，需要说明的是，3D-VAR中没有时间的概念，因此这里的并不是真正的时间，而是为用扩散方程进行滤波而引入的“虚拟”的概念。

推广至二维有限区域，扩散方程可改写为：

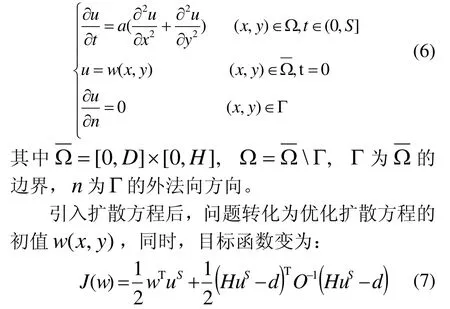
3.2 伴随方程及目标函数的梯度

在基于梯度的优化算法中，需要知道目标函数关于控制变量的梯度。引入了热扩散方程，便可以利用变分伴随方法推导出梯度的表达式。通常来讲，应该从离散的扩散方程直接推导出离散的伴随方程和目标函数梯度，但限于篇幅，本文仅给出连续形式的伴随方程及梯度表达式，并略去推导过程。同时，为便于叙述，假设观测点位于分析网格点上，O为单位矩阵，并暂时略掉背景项。可以证明，基于上述假设，伴随方程有如下形式：

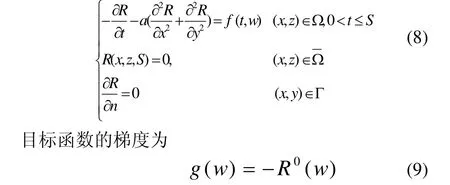
3) 计算 f。

5) 采用合适的最小化算法优化w。

6) 转至步骤2），直至满足收敛条件。

3.3 3D-VAR不能提取多尺度观测信息的原因分析

以下将基于扩散滤波分析3D-VAR不能有效提取多尺度观测信息的原因。

显然，伴随模型（8）也是扩散方程，因此梯度的求解过程实际上是对进行高斯滤波，滤波的强弱由扩散系数所决定。由于在有观测的分析网格点上而在无观测的网格点上，所以在空间的分布存在“跃变”。当滤波参数 a比较大时，滤波效果比较强，因此可以滤掉在空间的“跃变”，使得梯度比较平滑并保持物理上的连续性，但滤波参数大，同时意味着将滤除许多有价值的短波信息；而当a比较小时，则无法滤除的这种“跃变”，从而导致梯度在空间上的不连续性分布。显然，这种现象并不是物理上真实存在的，而是由观测数据的空间分布造成的。如果将此梯度直接应用于优化算法（例如最速下降法、共轭梯度法、L-BFGS方法等）进行三维变分分析，在观测稀疏的区域将得到错误的结果。

以最速下降法为例，其以在当前迭代点的梯度负方向作为下一次迭代的搜索方向，即：其中搜索步长可由线性搜索算法计算得到。由于梯度存在“跃变”，因此新的迭代值也会存在“跃变”，如此迭代下去，最终的分析结果在观测稀疏的区域会失去观测的长波特征。其他通用的优秀的最优化算法，如共轭梯度法、L-BFGS方法等，其设计也主要基于收敛速度的考虑，并不考虑尺度信息，因此应用于三维变分分析时存在与最速下降法同样的问题。

因此，由观测引起的目标函数梯度的空间不连续分布，是导致传统3D-VAR（包括相关尺度法、递归滤波法）无法提取多尺度观测信息的根本原因。

4 多尺度扩散滤波三维变分

基于扩散滤波思想，我们对3D-VAR进行了改进，将观测的尺度信息融入最优化算法中，设计了多尺度三维变分分析方法，以下简称多尺度3D-VAR。算法基本步骤如下：

3) 计算 f。

7) 减小扩散系数b。

8) 转至步骤2），直至满足收敛条件。

下面对此算法进行简要的分析：

需要指出的是，虽然此算法中的每一迭代步都对梯度进行各向同性扩散滤波，但由于滤波系数随迭代过程变化，依次提取不同尺度信息，因此整个优化过程的累积效果，实际带有非均匀各向异性滤波的特征，即可以在观测稀疏的区域及其周边区域进行较强的滤波以提取长波信息，而在观测数据密集的区域进行较弱的滤波以便不丢失短波信息，本文后面的试验结果也证明了这一点。

5 海表面温度数据同化试验

为检验多尺度3D-VAR提取观测信息的能力，我们分别将递归滤波3D-VAR及多尺度3D-VAR应用于SST二维数据同化试验，并对两者进行比较。

5.1 试验数据及参数设置

（1）“真实”场、观测数据及相关参数

分析区域为200˚E～220˚E，30˚N~40˚N，分析网格的分辨率为 0.25˚×0.25˚。图1a为我们假设的“真实”场，来源于2001年2月2日的AVHRR SST数据（AVHRR Pathfinder Version 5.0）。起初，在分析区域内随机选取500个观测, 然后人为地去掉位于 205˚E～209˚E，35˚N～38˚N区域内的观测，剩余466个观测（其分布见图1b），下面的试验中将用这些观测对真实场进行重建，以此检验多尺度3D-VAR在观测稀疏的区域提取观测信息的能力。假设观测误差不相关，故R为对角阵，这里假定为单位阵。观测算子H取为双线性插值算子。

（2）多尺度3D-VAR的差分格式及相关参数

多尺度 3D-VAR中扩散方程（6）的差分格式采用ADI格式（交错方向隐格式），可以证明，离散的伴随方程应采用LOD格式(局部一维格式)，而且扩散方程及伴随方程的差分格式绝对稳定，限于篇幅，证明此处略。扩散系数取0.2，扩散系数取为下面的高斯函数:

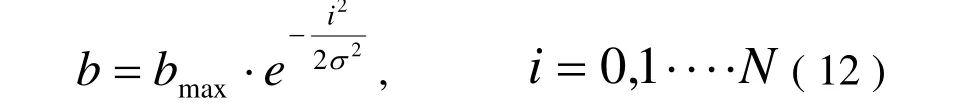
（3）优化算法

递归滤波3D-VAR中的优化算法采用L-BFGS (Liu and Nocedal, 1989)方法；多尺度3D-VAR中采用的线性搜索算法基于 Jorge J.More和 David J.Thuente的研究（Jorge J.More和David J.Thuente，1992）。

5.2 试验结果

图2a, 2b, 2c, 2d, 2e为递归滤波3D-VAR的分析结果，其滤波系数分别取α=0.2，0.3，0.4，0.5，0.6；图2f为多尺度3D-VAR的分析结果，扩散系数取为 0.2。与“真实”场（图1a）相比较可以看出，在递归滤波3D-VAR中，α的选取是非常困难的，若α过小，在观测稀疏的区域难以提取观测的长波信息；若α过大，会牺牲掉许多短波观测信息。然而，在多尺度3D-VAR中，无论长波还是短波观测都能很好地被提取出来。

为了更清楚地显示多尺度3D-VAR提取多尺度观测的过程，图4给出了迭代过程中分析场及下降方向的变化，迭代步分别为第10，20，40，60，80，160步。为便于比较，图3还给出了递归滤波3D-VAR的相应结果，其优化算法采用最速下降法，迭代步分别为第10，20，40，60步，滤波系数α取为0.2。可以看出，在递归滤波 3D-VAR 中，当α比较小时，在无观测（或观测稀疏）的区域，由于下降方向（采用最速下降法时其下降方向即为负梯度方向）缺乏长波结构（图3b，3d，3f，3h），从而导致分析场（图3a，3c，3e，3g）同样在此区域不能反映观测场的长波。事实上，若递归滤波3D-VAR中采用其它的优化算法，例如 L-BFGS、共轭梯度法等，依然会存在同样的问题。而图4a，4c，4e，4g，4k，4m，表明，多尺度3D-VAR方法可以从长波至短波依次提取观测信息，这是由于算法中的下降方向（图4b，4d，4f，4h，4l，4n）是对梯度进行高斯滤波得到的，弥补了梯度在观测稀疏的区域存在的缺陷。

图1 真实海温场（a）及观测的分布（b）Fig.1 (a): 图 True temperature field (b): Distribution of observations

图2 递归滤波3D-VAR及多尺度3D-VAR的分析结果。(a), (b), (c), (d), (e)分别为滤波系数α=0.2, 0.3, 0.4, 0.5, 0.6时递归滤波3D-VAR的分析结果；(f)为多尺度3D-VAR当扩散系数a= 0.2时的分析结果Fig.2 Analysis results of the recursive filter 3D-VAR and the multi-scale 3D-VAR.(a), (b), (c), (d) and (e) are for the recursive filter 3D-VAR with α=0.2, 0.3, 0.4, 0.5, and 0.6 respectively; (f) is for the multi-scale 3D-VAR with a=0.2.

图3 采用最速下降法的递归滤波3D-VAR的分析场（左列）及目标函数下降方向（右列）。其中，滤波系数α=0.2，迭代步数分别为10, 20, 40, 60Fig.3 Analysis results (left) and the descent direction (-g) (right) at iteration 10, 20, 40 and 60 using the steepest descent algorithm for the recursive filter 3D-VAR

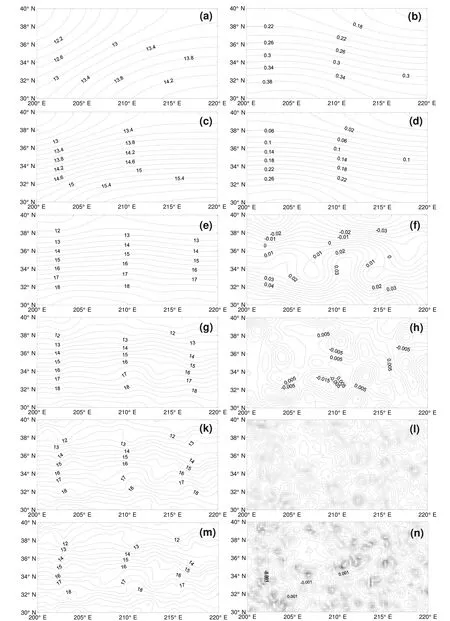
图4 多尺度3D-VAR的分析场（左列）及目标函数下降方向（右列）。其中，扩散系数a=0.2，迭代步数分别为10, 20, 40, 60, 80, 160Fig.4 Analysis results (left) and the descent direction (right) at iteration 10, 20, 40, 60, 80 and 160 using the multi-scale 3D-VAR ( a=0.2)

6 结 语

本文将扩散滤波引入三维变分分析，并与最优化算法相结合，提出了基于扩散滤波的多尺度三维变分方法，克服了传统三维变分难以提取多尺度观测信息的缺陷。应用于二维海温SST同化试验，效果良好。本文主要结论概括如下：

(1)传统三维变分难以很难有效提取多尺度的观测信息。由背景误差的非均匀和各向异性特征，理论上讲，3D-VAR中的相关尺度或滤波系数也应为非均匀及各向异性，且应根据误差统计确定。但在实际应用中，由于我们无从确切地知晓物理量的真实状态，因而据此进行的误差统计也很难保证其准确性和合理性。而若简单地以各向同性滤波器（如各向同性的递归滤波器）来模拟背景误差协方差的作用，则不能根据观测自动调整滤波行为，无法提取多尺度观测信息。

(2)3D-VAR中求解梯度的过程实际是滤波过程。当滤波系数很小时，在优化算法迭代的每一步，梯度在物理意义上代表当前解的观测余量。因而，纵观优化算法的整个迭代过程，所有的观测信息实际上都包含在这些梯度之中，从而使得我们可将滤波与优化算法相结合，对梯度进行滤波以提取需要的观测信息，这是本文算法的基础。

(3)由观测数据引起的目标函数梯度在空间的不连续分布，是导致传统三维变分方法无法提取多尺度观测信息的根本原因。如果将此梯度直接应用于传统的最优化算法（例如最速下降法、共轭梯度法、L-BFGS方法等）进行三维变分分析，在观测稀疏的区域有可能导致错误的结果，其原因是这些优秀算法的设计主要基于收敛速度的考虑，并不考虑尺度信息。

(4)本文提出的多尺度3D-VAR方法，从另一个角度看实际也是一种适用于多尺度变分分析的优化算法。在迭代的每一步，对梯度进行高斯滤波，作为新的线性搜索方向，而高斯滤波算子的正定性保证了此方向必为下降方向。滤波系数随迭代次数的增加而减小，从而可从长波至短波依次提取多尺度的观测信息。虽然，与现在通用的高效优化算法（如L-BFGS）相比，收敛速度尚有欠缺，但至少启发我们：适用于变分分析的优化算法既要考虑算法的收敛速度，也应考虑尺度信息，需要两者之间的平衡。

(5)多尺度 3D-VAR虽然在每一迭代步采用的是均匀的各向同性滤波，但从整个优化过程的累积效果看，实际带有非均匀各向异性的特征，因此即使在观测稀疏的区域也能捕捉到观测的长波信息，同时又不会损失观测密集区域的短波信息。

[1]Behringer D W，Leetmaa M J.A.An improved coupled model for ENSO prediction and implications for ocean initialization.Part I: the ocean data assimilation system[J].Mon.Wea.Rev，1998，126：1013-1021.

[2]Courtier P.Variational methods[J].Meteor.Soc.Japan，1997，75：211–218.

[3]Derber J，Rosati A.A global oceanic data assimilation system[J].Phys.Oceanogr，1989，19：1333–1347.

[4]Daley R.Atmospheric Data Assimilation[M].Cambridge University Press，1991：457.

[5]More J J，Thuente D J.On line search algorithms with guaranteed sufficient Decrease[R].Mathematics and Computer Science Division Preprint MCS-P330-1092. Argonne National Laboratory(Argonne,IL)，1992.

[6]Hayden C M，Purser R J.Recursive filter for objective analysis of meteorological fields: Applications to NESDIS operational processing[J].Appl.Meteor，1995，34：3–15.

[7]Huang X Y.Variational analysis using spatial filters[J].Mon.Wea.Rev，2000，128：2588–2600.

[8]Liu D C，Nocedal J.On the limited memory BFGS method for large scale optimization methods[J].Mathematical Programming，1989，45：503-528.

[9]Lorenc A C.Analysis methods for numerical weather prediction[J].Quart.Roy.Meteor.Soc，1986，112：1177–1194.

[10]Lorenc A C.Optimal nonlinear objective analysis[J].Quart.J.Roy.Meteor.Soc，1988， 114：205-240.

[11]Lorenc A C.Interactive analysis using covariance functions and filters[J].Quart.J.Roy.Meteor.Soc，1992，118：569–591.

[12]Purser R J，Wu W S，Parrish D.Numerical aspects of the application of recursive filters to variational statistical analysis.Part I: Spatially homogeneous and isotropic Gaussian covariances[J].Mon.Wea.Rev，2003a，131：1524–1535.

[13]Purser R J，Wu W S，Parrish D.Numerical aspects of the application of recursive filters to variational statistical analysis.Part II: Spatially inhomogeneous and anisotropic general covariances[J].Mon.Wea.Rev，2003b，131：1536–1548.

Multi-scale 3D-VAR based on diffusion filter

Li Dong1, Wang Xi-dong1,2, Zhang Xue-feng1,2, Wu Xin-rong1,2, Li Wei1, Han Gui-jun1

（1.Key Laboratory of Marine Environmental Information Technology, SOA, National Marine Data and Information Service, Tianjin 300171, China; 2.Key Laboratory of Tropical Marine Environmental Dynamics(LED),South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301,China)

P731.22

A

1001-6932(2011)02-0165-08

2009-11-23；收修改稿日期：2010-12-07

国家重点基础研究发展计划课题(2007CB816001)和国家自然科学基金项目（40776016、41030 854和40906016）联合资助。

李冬(1974-)，男，研究员，现主要从事海洋数据同化、并行计算及科学数据可视化研究。电子邮箱：lidong2003@gmail.com。