波高与风速联合概率分布研究

陈子燊

（中山大学水资源与环境系，广东 广州 510275）

波高与风速联合概率分布研究

陈子燊

（中山大学水资源与环境系，广东 广州 510275）

基于copula函数论述了两变量的联合概率分布方法。此方法的主要优点是边缘分布可由不同的分布函数构成，变量间可具相关性。以粤东汕尾海域极值波高与相应风速为研究实例，经分析获得以下结果：(1) 优选的极值波高和风速可分别由P-III型和GEV分布表示； (2) 拟合优度检验指标表明二者的最优连接函数为Archimedean copula类的Gumbel-Hougaard copula；(3) 与联合分布比较，重现期介于5—200年之间的波高边缘分布设计值的相对差值大约介于3.1% ～ 8.1%之间，风速设计值相对差值大约介于2.8% ～6.4%之间；(4) 特定风速设计频率条件下，波高与风速的遭遇概率随波高设计频率的减小而减小，特定波高设计频率随风速条件频率的减小，二者的遭遇概率随之增大。

极值波高和风速；边缘分布；联合概率分布；Copula函数；条件分布

Abstract：This article introduced the method of bivariate joint probability distribution based on the copula function.A major advantage of this method is that marginal distributions of individual variables can be of any form and the variables can be correlated.Some of conclusions were reached by using extreme wave height and wind speed as an example collected in Shanwei sea area as the following: (1) Optimized marginal distributions of wave height and wind velocity can be represented by the Pearson pattern three and generalized extreme value distribution, respectively; (2) Gumbel–Hougaard Copula that belongs to Archimedean copula family was the optimal copula selected by the goodness-of-fit test; (3) The relative differences of the special frequency design values between the marginal distribution of wave height and the joint distribution fall in between 3.1% and 8.1% for the return periods between 5 and 200 years, and the relative differences of wind velocity fall in between 2.8%～6.4%; (4) The encountering probabilities of wave height given wind velocity decrease along with decreasing the frequency of wave height; whereas the encountering probabilitiy increase while the specific wave height frequency is along with decrease of wind velocity frequency.

Keywords：extreme wave height and wind velocity; marginal probability distribution; joint probability distribution; copula function; conditional probability distribution

全球暖化可能导致出现极端气象事件的频率和强度加大，甚则常态化，此对于海岸和海洋工程安全构成极大威胁。众知，风浪的形成与发展主要是由风直接作用下的海洋动力过程。大浪与极端风速密切相关，也都是造成海岸工程损毁和海岸侵蚀的重要动力因子。深入分析极值波高和风速的联合概率分布对海岸工程与海岸防护的规划设计和风险控制十分重要。

至今已有一些多变量联合概率分布应用于海洋水文气象要素的研究。如，周道成应用耿贝尔逻辑模型描述了年极值风速和有效波高两随机变量的联合分布[1]；董胜采用边缘分布为皮尔逊Ⅲ型的联合分布估计了年极值有效波高与风速的联合出现概率[2]；潘锦娥使用对数正态分布探讨了波高与周期的联合分布[3]。然而，采用传统的多变量联合概率分布时存在一定的约束条件，其要求各个边缘分布函数类型与多变量分布函数类型一样，而且各个边缘分布必须完全相同。而且，不同的水文气象要素或不同空间位置的同一水文气象要素通常并不服从同一分布，水文气象要素的正态分布也难以满足。这使得传统的多变量分布函数的概率分析受到较大限制。近十年来，解决多变量联合概率分布的一个强有力工具的Copula 函数已被广泛应用于金融工程领域，国内外在陆地水文气象领域也得以较多应用[4-12]，但国内在海洋水文气象领域的研究还仅见于参考文献[13]。本文将在论述Copula函数主要理论与方法基础上，应用实例构造二变量水文气象要素的联合概率分布模式，深入分析水文气象变量间的概率分布主要特征。

1 基于 Copula函数的联合概率分布模型

1.1 Copula函数、参数估计和拟合优度评价

Copula的数学涵义是指把多个变量的联合分布与它们的边缘分布连接在一起的函数。根据奠定Copula函数理论基础的Sklar定理，令F是具有单变量边缘分布函数的n维分布函数，若边缘分布函数连续，则存在一个唯一满足关系的连接函数。相反，如果C是一个n 维Copula函数，n维分布函数。作为一新的概率分布和统计推断方法，Copula函数为描述多变量随机变量之间的相关结构提供了一个新技术手段而得到了广泛应用，曾系统地总结了Copula函数的性质和这个领域的主要研究成果。

根据Copula函数性质，构建两变量的联合概率分布模型可分两步进行：首先分别确定边缘分布然后选择一个能够恰当地反映变量间相关结构的Copula函数式中，在三大类Copula函数——椭圆型、阿基米德型(Archimedean)和二次型中，阿基米德(Archimedean) Copula是由其生成元唯一确定的单参数函数，是当前应用于水文气象领域的一类非常重要的Copula函数。几种常用的二维Archimedean Copula函数及其适用性如下：

与AMH Copula函数类似，但对相关性程度没有限制。Frank Copula结构具有对称性，即在其分布的上尾和下尾，变量间的相关性呈对称增长。

Copula参数θ的估计方法大致可分为3种：①相关性指标法：根据Kendall秩相关系数与θ的关系间接求得；②适线法：在一定适线准则下, 求解与经验点据拟合最优的频率曲线的统计参数；③极大似然法。由于不同的Copula 函数代表不同的相关结构，对Copula 函数的选择将直接影响到一些分析和统计推断的结果[15]，因此选择合适的Copula函数显得十分重要。择优选用Copula函数的主要检验方法有由图示直观选择Copula 函数的Genest–Rivest方法[16]、均方根误差(RMSE)准则法和AIC信息准则法等。

1.2 联合概率分布及其重现期

使用“或”符号“∨”，以及“和”符号“∧”，两个单变量事件理论上可以组合成八种两变量事件。

对于极端水文气象事件，关注的主要是以下两种两变量事件：

同理，还可定义给定随机变量X≥x和X≤x条件下的随机变量Y的4个条件概率。

2 实例研究

2.1 基本数据

基本数据采用位于粤东汕尾海域的汕尾海洋观测站 1972—1992年观测的历年热带气旋影响期间E向浪的最大波高与相应的极端风速。样本的基本统计特征值表明，最大风速为45 m/s，达到强台风等级，最大波高为9.50 m。极值波高及其相应的极值风速的偏态系数分别为1.21和1.10，都属于正偏分布。

2.2 联合分布计算与分析

2.2.1 边缘分布函数 对两样本的边缘分布，都使用了以下两个三参数的概率分布函数择优：

a、广义极值分布(GEV)：

表1 边缘分布参数与优度检验值Tab.1 Parameters of the marginal distribution and the values of goodness of fit test

2.2.2 Copula 函数的参数估计及拟合优度评价样本波高与风速的Kendall秩相关系数 (τ) 计算值为 0.629，说明二者具有较高的相关性。采用相关性指标法计算了样本的联合概率分布的copula参数θ，并利用AIC、RMSE检验其拟合优度，结果见表2。根据拟合优度评价指标，选择样本中AIC和 RMSE最小、KT-Ke关系图中点据和理论直线最接近45°对角线的GH Copu1a函数作为联合概率分布的连接函数（为节省篇幅，KT-Ke关系图略），由此构建的极值波高和极值风速的GH Copula联合分布函数如下：

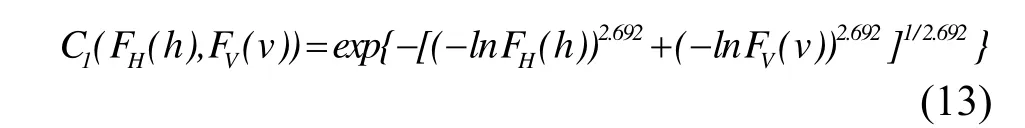
图1 两变量边缘分布图：波高（左图），风速（右图）Fig.1 Diagrams of marginal distribution of wave heights (left panel) and wind velocities (right panel) in the sample one.

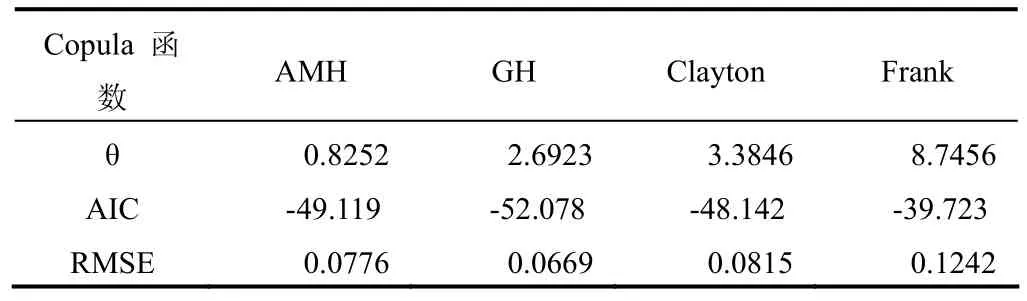
表2样本的Copula参数及拟合优度评价指标Tab.2 Parameters of Copula functions and the evaluation indices of goodness of fit for the sample

2.2.3 联合概率分布与重现期 极值波高和极值风速的联合概率分布、联合重现期和同现重现期见图2所示，不同重现期的设计波高和设计风速见表3。显然，波高风速联合重现期小于边缘分布重现期，边缘分布重现期则小于同现重现期。按照同频率原理，即单变量推算的设计值小于波高风速联合重现期设计值，差值随重现期减小而有所增大，重现期5-200年的波高设计值相对差值大约介于3.1% ～ 8.1%，风速设计值相对差值大约介于2.8% ～ 6.4%。以100年一遇波高为例，波高、风速边缘分布设计值分别为12.05m和同频率的联合分布设计值分别为12.57m和单变量边缘分布50年一遇和100年一遇的同现重现期分别为70年和141年。上述结果表明，如以波高风速联合概率分布为设计值，单变量无论是波高或风速推算的设计值实际上没有达到设计标准。

图2 联合概率分布三维图（左图）、联合重现期(年)等值线图（中图）、同现重现期(年)等值线图（右图）Fig.2 Diagrams of joint probability distribution (left panel), joint return period (middle.panel) and occurrence period (right panel)

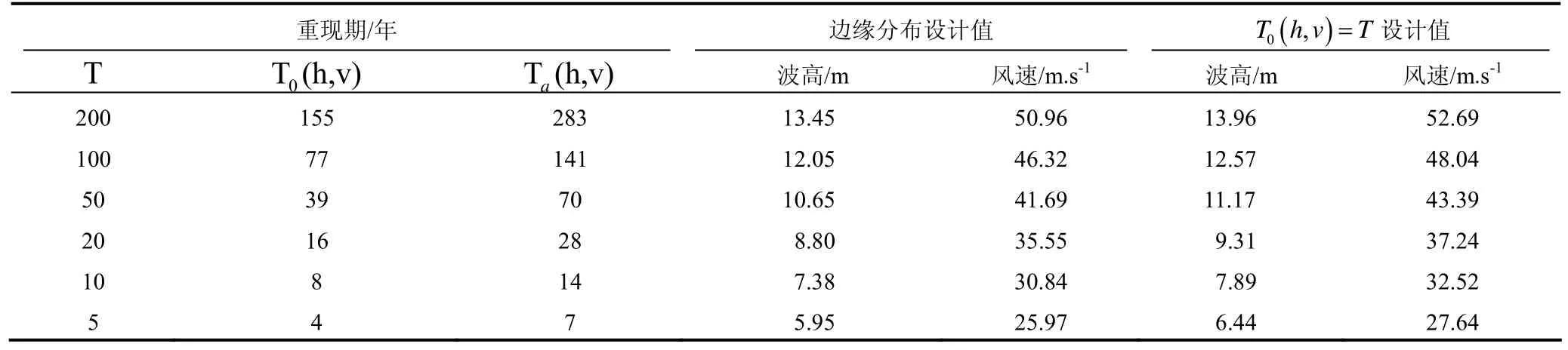
表3 不同重现期设计波高和设计风速值Tab.3 Designed values of different return periods of wave height and wind velocity

2.2.4 条件概率分布与遭遇分析 分别考虑条件概率 1：和条件概率 2：两种条件概率，其中，条件概率 1指的是，当发生超过某一标准的风速v时，出现超过某一标准波高h的概率；而条件概率2的涵义则为发生不超过某一标准的风速v时，出现大于某一标准波高h的概率。二者的实质都是反映极值波高与相应风速的遭遇概率。两种不同条件概率的计算结果见表4。表4显示，特定风速设计频率条件下，随波高设计频率的减小，二者的遭遇概率也随之减小；反之，特定波高设计频率随风速条件频率的减小，二者的遭遇概率随之增大。条件概率1表明，同频率下的极端波况和相应风况的遭遇概率不小于70%。如：设计频率超过20%的波高与设计频率超过10%风速的遭遇概率为91.6%，而设计频率都为10%（重现期10年）时，二者的遭遇概率为72.6%。条件概率2则表明，当设计风速小于某一定值时，相对于条件概率 1，极端波况和相应风况的遭遇概率明显减小，同频率下极端波况和相应风况的遭遇概率都不大于7%。如：设计频率超过20%的波高与设计频率小于10%风速的遭遇概率为12.0%，而设计频率都为10%（重现期10年）时，二者的遭遇概率为3.0%。此对于如何在海岸工程选择与设计波高相匹配的设计风速，需要综合考虑遭遇概率小（风险小安全率高）和工程规模投入资金之间的平衡关系。因此需要在安全、资金投入与产出效益之间寻求平衡点，此需经过严格的经济分析与多方案综合比较才能确定。

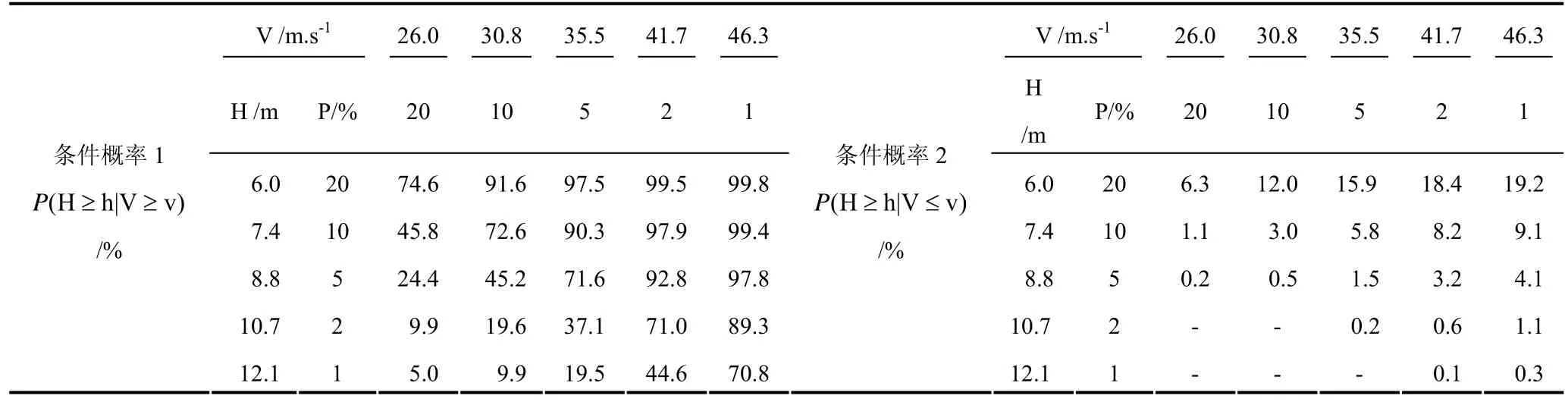
表4 两种条件概率计算结果*Tab.4 Computed results of conditional probability of two types

3 结 语

本文以粤东汕尾海域的台风影响下的海况为实例，基于Copula理论与方法构建了波高和相应风速的联合概率分布模型。分析表明，两变量联合分布比单变量分布能更全面地反映极端海况条件下的重现水平，根据极端海况下的波高与风速的遭遇概率的风险分析可更好地为海岸工程规模的规划设计、资金投入和风险控制之间的均衡考虑提供科学依据。

[1]周道成, 段忠东.耿贝尔逻辑模型在极值风速和有效波高联合概率分布中的应用 [J].海洋工程, 2003, 21(2): 45-51.

[2]董胜, 丛锦松, 余海静.涠洲岛海域年极值风浪联合设计参数估计 [J].中国海洋大学学报, 2006, 36(3): 489-493.

[3]潘锦娥.显著(或有效)波高与平均周期的长期联合分布探讨 [J].海洋通报, 1989, 8(3): 1-10.

[4]刘曾美, 陈子燊.区间暴雨和外江洪水位遭遇组合的风险 [J].水科学进展, 2009, 20(5): 619- 625.

[5]闫宝伟, 郭生练, 肖义, 等. 基于两变量联合分布的干旱特征分析 [J].干旱区研究, 2007, 24(4): 537- 542.

[6]方彬, 郭生练, 肖义, 等.年最大洪水两变量联合分布研究 [J].水科学进展.2008, 19( 4): 505-511.

[7]陆桂华, 闫桂霞, 吴志勇, 等.基于 copula函数的区域干旱分析方法 [J].水科学进展, 2010, 21(2): 188-193.

[8]Zhang L, Singh V P.Bivariate rainfall frequency distributions using Archimedean copulas [J].Journal of Hydrology, 2007, 332: 93-109.

[9]Shiau J T, Song F, Nadarajah S.Assessment of hydrological droughts for the Yellow River, China, using copulas [J].Hydrological Processes, 2007, 21: 2 157-2 163.

[10]Favre A C, Adlouni S E, Perrault L, et al.Multivariate hydrological frequency analysis using Copulas [J].Water resources research, 2004, 40.

[11]Joe H.Multivariate Models and Dependence Concepts [M].Chapman & Hall, London, 1997.

[12]郭生练, 闫宝伟, 肖义, 等.Copula 函数在多变量水文分析计算中的应用及研究进展 [J].水文, 2008, 28(3): 1-7.

[13]秦振江, 孙广华, 闫同新, 等.基于Copula函数的联合概率法在海洋工程中的应用 [J].海洋预报, 2007, 24(2): 83-90.

[14]Nelsen R B.An Introduction to Copulas.Springer Series in Statistics [M].Springer, NewYork, 1999:216.

[15]Embrechts P, Lindskog F, McNeil A.Modeling Dependence with Copulas and Applications to Risk Management Handbook of Heavy Tailed Distributions in Finance [M].Elsevier Science, Publishers, New York, 2003: 329–384.

[16]Genest C, Rivest L.Statistical inference procedures for bivariate Archimedean copulas [J].Journal of American Statistical Association, 1993, 88:1 034-1 043.

Study on joint probability distribution of wave height and wind velocity

CHEN Zi-shen

（Department of Water Resource and Environment，Zhongshan University，Guangzhou 510275，China）

P731.22

A

1001-6932(2011)02-0159-06

2010-08-30；收修改稿日期：2010-09-20

国家自然科学基金资助项目( 40576041)。

陈子燊, (1952―), 男, 福建福州人, 教授, 研究方向: 河口海岸环境。 电子邮箱: eesczs@mail.sysu.edu.cn。