基于能量传递的Er3+浓度猝灭效应分析

刘永皓，佟 欣

(1.大庆师范学院 物理与电气信息工程学院，黑龙江 大庆 163712； 2.大庆师范学院 数学科学学院，黑龙江 大庆 163712)

0 引言

激活离子在基质中的荧光浓度猝灭效应对于材料的发光和激光性能有着直接而重要的影响。浓度猝灭是这样一个过程：随着激活离子浓度的提高，离子之间的距离减小，相互作用增强，从而使能量转移到猝灭中心的几率大大增加，发光效率下降。Er3+离子浓度是EDFA用材料设计中所要考虑的重要参数，因为它决定了实现特定增益所需的光纤长度和泵浦功率[1]。近年来，Er3+掺杂的1550nm微片激光器和平面光波导放大器由于体积小，结构紧凑等优点受到了普遍的关注[2]，这种激光器要求基质玻璃中有足够高的Er3+离子浓度来吸收泵浦光能量，提高单位长度的增益。然而，过高的掺杂浓度往往会引起强烈的荧光浓度猝灭效应，导致Er3+离子荧光寿命降低。

1 理论模型

1.1 Forster-Dexter 模型

1948年，Forster[3]首先提出了基于电偶极相互作用的无辐射共振能量传递理论，Dexter[4]后来发展了这一理论，包括了高阶的电多极相互作用和交换作用并得到了广泛的应用和推广。Forster-Dexter模型主要考虑施主与受主之间的直接能量传递过程，忽略了施主间的能量迁移。对于电偶极-电偶极相互作用，根据Forster-Dexter模型，可以通过施主的发射截面和受主的吸收截面来计算两种重要的能量传递参数：能量传递临界距离R0及能量传递微参量CDD和CDA。临界距离是指能量传递效率为50%时施主与受主之间的距离，它可以定性地说明能量传递发生的难易程度，可以由下面的公式计算：

(1)

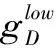
CDD和CDA分别是衡量施主之间及施主与受主之间相互作用的量，其中CDD可以看作是受主即为施主自身时CDA的一个特例。根据这两个参量可以估计材料中能量迁移及能量传递的强弱，这两个参量可由下面的公式计算：

(2)

(3)

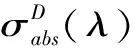
1.2 Auzel模型

荧光浓度猝灭源于能量传递过程，浓度猝灭的分析必须区分不同的能量传递途径。一般情况下Er3+离子的浓度要高于猝灭中心OH-基团的浓度，距离OH-基团较近的Er3+离子通过直接弛豫而发生猝灭，距离其较远的则可由能量迁移的方式迁移到邻近Er3+离子的位置而发生猝灭。因此Er3+离子的弛豫方式一般分为受限扩散弛豫和快速扩散弛豫两种情况。Auzel分别对这两种情况进行了分析，并在偶极-偶极相互作用的机制下建立了相应的浓度猝灭模型[5-6]。

在受限扩散弛豫范围内，发生浓度猝灭时激活离子的荧光寿命可以根据下式计算

(4)

其中，τ0为不存在浓度猝灭时激活离子荧光能级的本征寿命；N是激活离子掺杂浓度；N0是浓度猝灭临界浓度，指以临界距离R0为半径的球内有一个相互作用的离子。

在快速扩散弛豫范围内，激活离子荧光寿命随浓度变化的表达式如下

(5)

其中β是与电声子耦合强度和基质声子能量相关的参量，△E为对应荧光衰减的上下多重态最低晶场能级间的能量差，一般可由吸收光谱直接得到。

2 主要结果

研究浓度猝灭需要测量不同Er3+离子浓度下4I13/2能级的荧光寿命。表1给出了由不同Er3+浓度的荧光衰减曲线根据单指数拟合得到的荧光寿命。从表1中可以看出，当Er3+离子浓度由0.1mol%增加到3.0mol%，荧光寿命明显缩短，由于自发辐射跃迁几率可以认为并不随Er3+掺杂浓度发生改变，这主要是无辐射跃迁几率不断增加造成的。

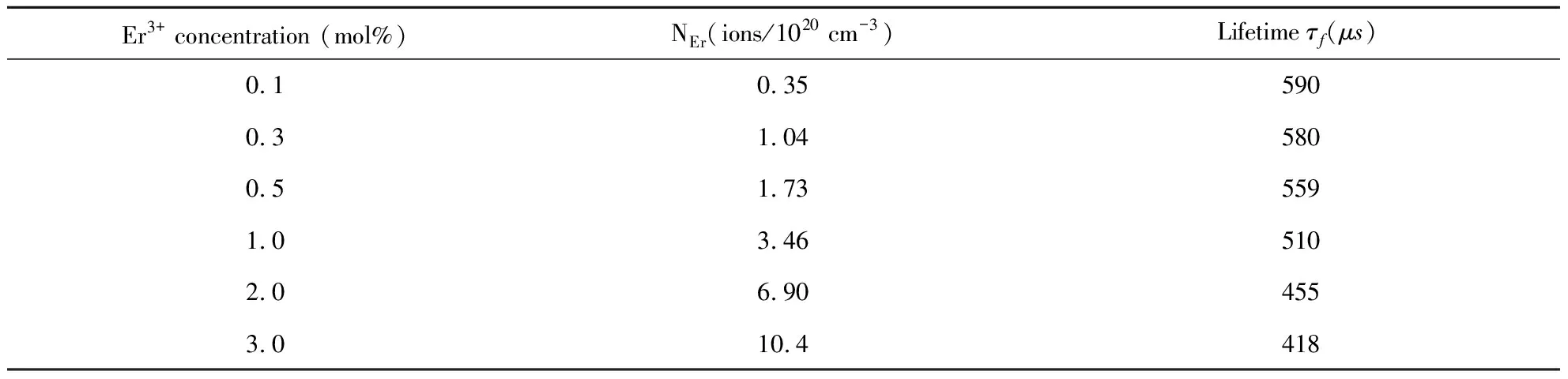
表1 不同Er3+离子浓度硼酸铋玻璃的荧光寿命

Er3+离子的无辐射跃迁几率Wnr主要来源于单个Er3+离子的多声子弛豫几率Wmp，Er3+和OH-基团间的能量传递几率WOH以及Er3+离子间交叉弛豫引起的合作上转换几率WET：

WNR=Wmp+WOH+WET

(6)

根据能隙指数定律可知，单个Er3+离子的多声子弛豫几率来源于Er3+离子与基质晶格振动之间的相互作用，在所讨论的浓度范围可以认为不随掺杂浓度变化[7]。WOH和WET则随着Er3+离子浓度的增加而增大，理论和实验均表明WET与Er3+离子浓度成平方关系，而WOH与Er3+离子浓度成线性关系[8]。图1给出了总的衰减几率随Er3+离子浓度的变化关系。从图1中可以看出，总的衰减几率随Er3+离子浓度的变化呈现了很好的线性关系，说明了体系中的浓度猝灭效应主要是由OH-基团引起的，WET对无辐射跃迁几率的影响可以忽略。

Er3+离子4I15/2→4I13/2的能量间隔约为6500cm-1，而OH-基团振动频率为2700～3700cm-1，因此只需要2～3个OH-声子就可以使Er3+离子由4I13/2能级无辐射弛豫到4I15/2能级，降低其荧光效率。OH-基团对Er3+离子的荧光猝灭示意如图2所示。荧光浓度猝灭可以被看作是一类特殊的能量传递过程，其中猝灭中心OH-基团为受主，Er3+离子为施主，因此猝灭几率由Er3+浓度NEr和OH-基团浓度NOH两方面决定。距离OH-较近的Er3+离子直接将能量传递给OH-而发生猝灭，距离较远的则先通过Er3+离子间的能量迁移到达OH-附近，再与OH-相互作用发生猝灭效应。随着Er3+浓度的增加，Er3+离子之间的能量迁移几率变大，这种单纯的能量迁移并不会导致激发态能量的损失，但却增加了到达猝灭中心OH-基团的几率。

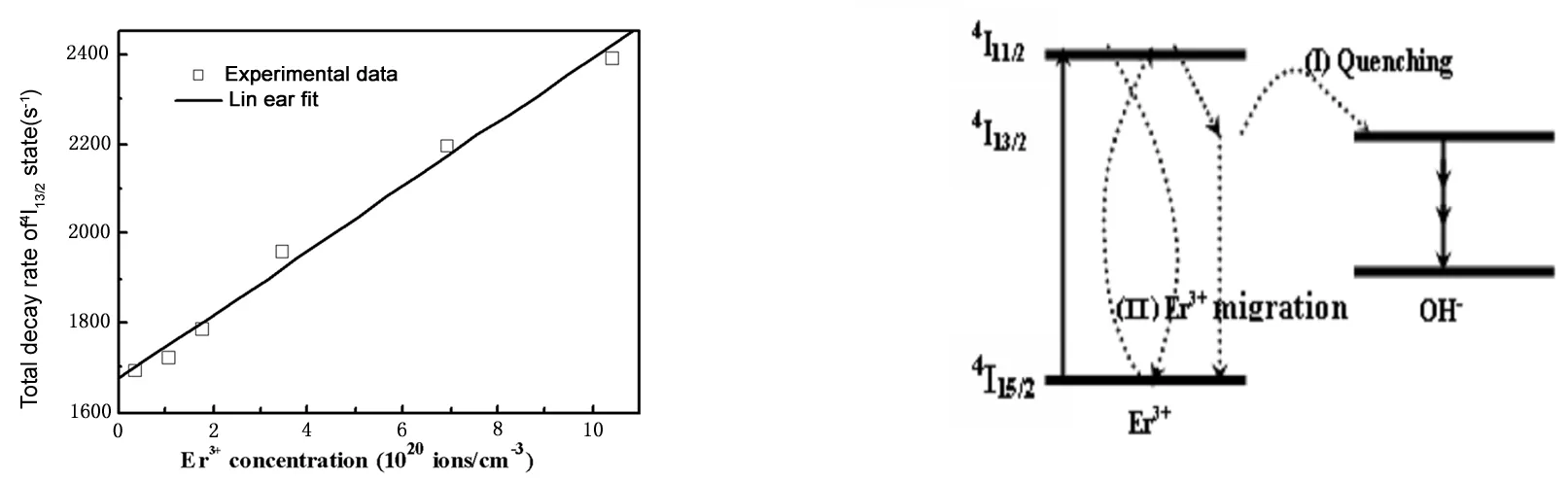
图1 硼酸铋玻璃总的衰减几率随Er3+离子浓度的变化关系 图2 OH-基团与Er3+离子的猝灭作用示意图

我们首先采用受限扩散模型对不同Er3+掺杂浓度下的荧光寿命进行了拟合。如图3所示，拟合曲线同实验值相差较大，这主要是受到高浓度数据点(NEr>3.46×1020cm-3)的影响，并由此初步推断此时Er3+离子的弛豫不在受限扩散弛豫范围内。图4给出的是在NEr≤3.46×1020cm-3时的四个实验点经(4)式拟合的曲线，可以看出拟合曲线与实验值符合得比较好，拟合得到τ0=586μs，N0=10.5×1020cm-3。Er3+离子在浓度最低(NEr=3.46×1019cm-3)的样品中荧光寿命为590μs，这与拟合得到的τ0是相近的。这是由于此时Er3+离子的掺杂浓度NEr远小于浓度猝灭的临界浓度N0，因此浓度猝灭效应对荧光寿命的影响较弱。这说明在较低浓度下(NEr≤3.46×1020cm-3)，Er3+离子的浓度猝灭机制为受限扩散弛豫。利用拟合得到的τ0和N0，代入(5)式对Er3+≥3.46×1020cm-3时的三个实验点进行了拟合，由于缺乏硼酸铋玻璃声子边带谱的相关数据，参数β的准确数值无法得到，在拟合时把它设为一个可调参量。图5所示的拟合效果图可以说明在较高Er3+离子浓度时的猝灭机制中，快速扩散弛豫占主导地位。从上面的拟合结果中还可以得到β为0.78×10-3cm，这与在偏磷酸盐玻璃中报道的结果(β=0.78×10-3cm)很接近，其主要原因可能是两者的声子能量和晶场强度相近造成的，一般认为在硼酸盐中声子能量约为1400cm-1，而在偏磷酸盐玻璃中声子能量也高达1340cm-1。图6给出的是分别采用受限扩散模型和快速扩散模型对实验点的拟合结果，从图中可以很清晰地看出，随着Er3+离子浓度的增加，体系中的浓度猝灭先后经历了受限扩散弛豫和快速扩散弛豫两种猝灭过程。其主要原因是：Er3+离子浓度较低时，Er3+间的能量迁移几率与Er3+到OH-的猝灭几率相比具有相同的量级，这时的浓度猝灭属于受限扩散弛豫；随着Er3+离子浓度的增大，Er3+间的距离减小，能量迁移几率变大，从而使猝灭几率小于能量迁移几率，进入快速扩散弛豫范围。

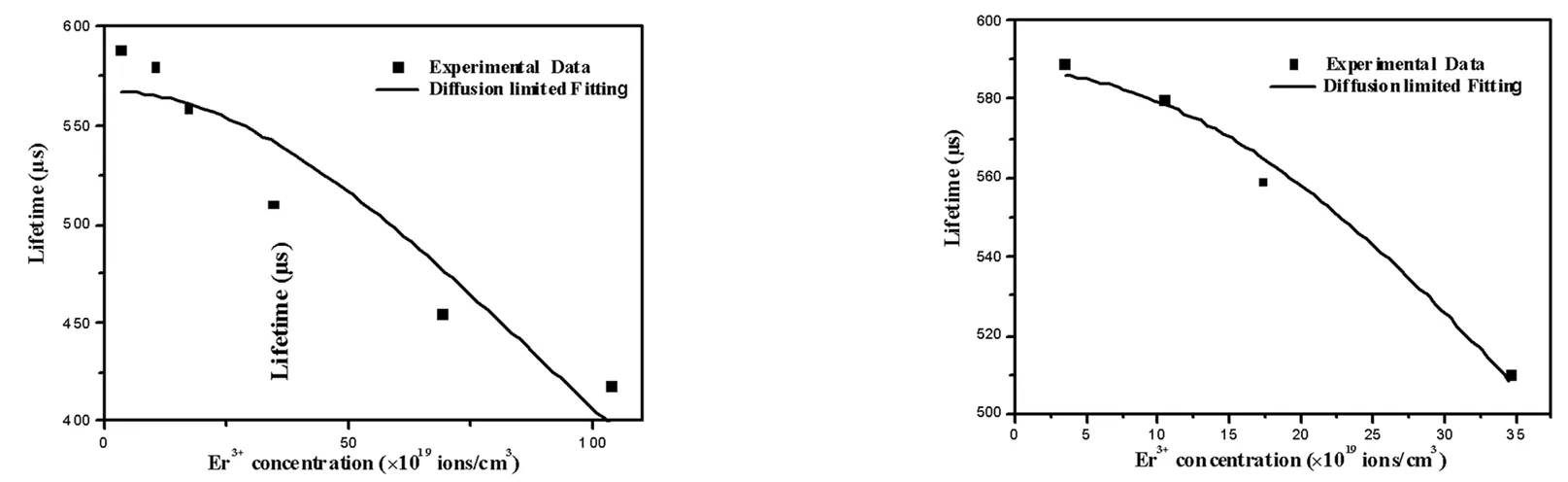
图3 所有荧光寿命实验点的受限扩散模型拟合 图4 NEr≥3.46×1020cm-3时荧光寿命实验点的受限扩散模型拟合

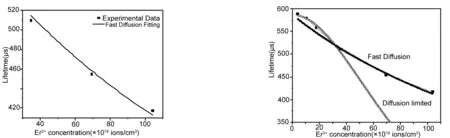
图5 NEr≥3.46×1020cm-3时荧光寿命实验点的快速扩散模型拟合 图6 受限扩散模型和快速扩散模型对荧光寿命实验点拟合结果的对比

3 结语

通过对系列Er3+掺杂浓度下荧光寿命点的拟合得到了体系的多声子驰豫几率，建立了Er3+基于OH-基团作为猝灭中心的浓度猝灭模型。根据Auzel的理论模型分析了浓度猝灭机制，拟合结果显示体系中的浓度猝灭过程先后经历了受限扩散弛豫和快速扩散弛豫两种猝灭过程。

[参考文献]

[1] G. Nykolak, P. C. Becker, J. Shmulovich, et al. Concentration dependent 4I13/2lifetimes in Er doped fibers and Er doped planar waveguides[J]. IEEE Photo. Tech. Let., 1993,5: 1014-1016.

[2] K. Hattori, T. Kitagawa, M. Oguma, et al. Erbium-doped silica-based waveguide amplifier integrated with a 980/1530 nm WDM coupler[J]. Electron. Lett., 1994,30: 856-857.

[3] T. Forster. Intermolecular eNErgy migration and fluorescence[J]. Annal. Phys., 1948,6: 55-75.

[4] D. L. Dexter. A theory of sensitized luminescence in solids[J]. J. Chem. Phys., 1953,21: 836-850.

[5] F. Auzel, F. Bonfigli, S. Gagliari, et al. The interplay of self-trapping and self-quenching fo resonant transition in solids; role of a cavity[J]. L. Lumin., 2001,94-95: 293-297.

[6] F. Auzel, A fundamental self-geNErated quenching center for lanthanide-doped high-purity solids[J]. L. Lumin., 2002,100: 125-130

[7] 罗遵度，黄艺东. 固体激光材料光谱物理学[M].福州：福建科学技术出版社，2003:55-76.