基于二元Box样条的周期多尺度分析构造

刘荣辉,沙元霞

(大庆师范学院 数学科学学院，黑龙江 大庆 163712)

0 引言

自从提出样条函数的概念以来，样条函数方法得到了迅速的发展和广阔的应用，尤其是Box样条函数，它具有结构简单，便于应用的特点，文章通过选取二元Box样条函数作为初始函数，给出了相应的周期多尺度分析构造。 通过周期多尺度分析，我们很容易得到各种多元小波，这对于数字信号的处理，微分方程与积分方程数值求解等实际问题的解决很有帮助。

1 预备知识

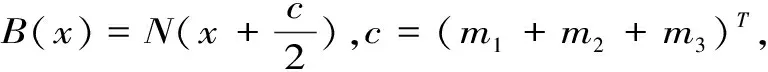
(1)

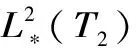
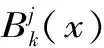
(2)

则由(1)，(2)两式可得如下命题1：

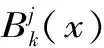
证明：1)对任意j≥0,k∈Z2，由中心Box样条的对称性，我们有

2)

3)

命题成立。

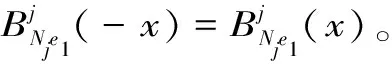
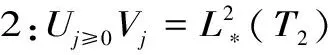
证明：令V=Uj≥0Vj我们只需证V⊥={0}

对任意的f(x)∈V,j≥0,λ∈Z2,有f(x-λhj)∈V，任取函数g(x)∈V⊥，则有0=〈f,g〉=〈f(-λhj),g〉。

设f(x)和g(x)的Fourier级数展开系数分别为{Sv}v∈z2,{λλ}λ∈z2，则我们有

从而

我们可得

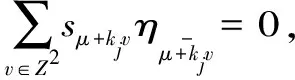
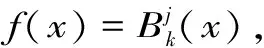
故

令j→∞，则有

故对所有的v∈Z2有ηv=0，这就蕴含着g(x)=0，即V⊥={0},命题成立。

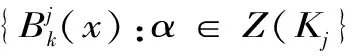
设常数{α}使得

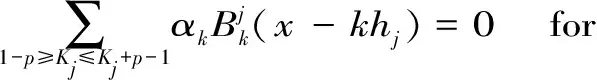
作变量代换y=2jx，可得

将y限制到子区间[m1T,(m1+1)T]×[m2T,(m2+1)T]上，我们有

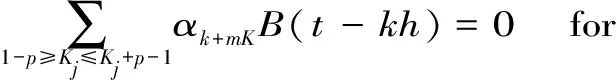
则很容易证出：

αk=0,1-p≤liKj+p-1,i=1,2

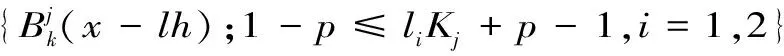
3 主要结果

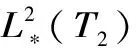
1)Vj⊂Vj+1,j≥0。

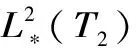
3)对任意j≥0，存在函数fj∈Vj，使得平移函数组{fj(▯-2-jk),k∈Z(Tj)}构成Vj的一组基底。

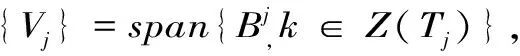
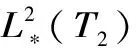
4 结语

通过上面的研究，我们得到了基于二元Box样条的周期多尺度分析的构造，在周期多尺度分析的基础上，很容易构造出具有基插值性质的小波函数，这在实际应用中是非常方便的，能够快速的处理信号问题，节省计算量。

[参考文献]

[1] 刘荣辉.关于二元Box样条的正交周期小波函数构造[J].大庆师范学院学报,2009,29(3):69-71.

[2] I. J. Schoemberg, Contribution to the problem of approximation of equidistant data by functions[J].Part A&B, Quart. Appl. Math.,1946,4:45-99.

[3] X. Z. Liang, G. R. Jin, H. L. Chen.Bivariate box-spline wavelets, in: Harmonic Analysis in China (M. T. Cheng etc. eds)[J].Kluwer Academic Publishers,1995,22:183-196.

[4] C. de Boor, K. HÖllig,S. Riemenschneider.Convergence of cardinal series[J].Proc. Am. Math. Soc.,1986,98:457-460.

[5] S. S. Goh, S. L. Lee， K. M. Teo Multidimensional periodic multiwavelets[J].J.Approx. Theory, 1999,98(1):72-103.