短波通信中的低复杂度时域均衡

，2

(1.解放军理工大学 通信工程学院,南京210007;2.解放军65043部队,吉林 松原 131500)

1 引 言

对于减小等概输入的数据序列的错误概率而言，最大似然序列估计(MLSE)是最优均衡技术[1,2]，其复杂程度随着码间串扰(ISI)长度和信号星座图的大小呈指数增长。现有文献所研究的其它均衡器，如线性均衡器或判决反馈均衡器等，虽然实现复杂度较低，但所获误比特率(Bit Error Rate，BER)性能却远劣于MLSE的BER性能[2]。

降低MLSE复杂度已成为当前研究的焦点[3-6]。文献[7]将逐符号的最大后验概率(Maximum A Posteriori，MAP)均衡和MLSE相结合;另外还有减少状态序列估计(Reduced-state Sequence Estimation，RSSE)的逐幸存路径处理(Per-survivor processing，PSP)[8-10]法和利用分集映射原理减小信号调制阶数法等。

近来，文献[11]将具有非连续性的差分移相键控(Differential Phase Shift Keying，DPSK)和球形译码算法相结合，实现了时变信道下未知参数的多符号差分检测(Unknown-statistics Multiple-symbol Differential Detector，MSDD-US)。但文献[12]已指出，基于球面译码算法的复杂度将随分组长度的增加呈指数增长，因而所获算法只适用于数据较短的情况。

本文提出的低复杂度时域均衡是一种基于Chase算法的准最大似然序列估计的均衡方法。在早期的文献中，Chase算法用来解决Turbo码和RS码的软判决译码。然而，Chase算法最直接的应用是产生多个检测图样，因此会带来复杂性的大幅增加。本文通过引入可信度概念，消除可能性小的幸存路径，同时利用滑动窗[13]实现小范围内的全搜索，有效地减小了码间串扰的影响。

2 MLSE算法

时间离散信道的输出信号可以写成：

(1)

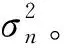
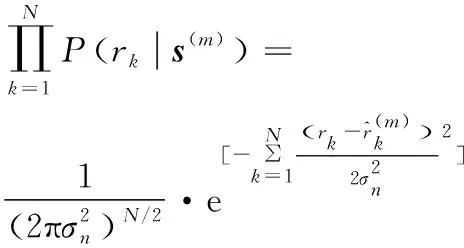
(2)

并选择似然概率最大的输入序列作为均衡器的输出。因为上式仅在指数项上有变量，因此只需使下式最小化即可：

(3)

最直接的方法是穷搜索，需要计算MN(M=2m为符号进制数)条路径的似然概率。实际中，用Viterbi算法代替穷搜索算法可将路径数减小到ML。但是对于码间串扰长的信道，这种算法太复杂。

3 Chase算法

Chase算法实现过程如下：

(1)由接收序列r获得相应的硬判决序列y和可信度序列Γ。y中元素的可信度定义为

(4)

(2)根据可信度最低的位置产生2p个试探序列k；

(3)构造测试序列x，其中x=y⊕k，⊕表示按位异或；

(4)对测试序列x进行硬判决译码，得到的候选码字c归入集合z；

(5)在集合z中寻找与接收序列r有最小欧氏距离的码字，作为译码器的输出。欧氏距离定义为

(5)

由上可见，Chase算法的复杂度主要取决于试探序列集合的大小和硬判决译码算法的复杂度。

4 Chase均衡

由于Viterbi算法存在固定译码时延一般为4L～5L[2]，难以实时跟踪信道变化，从而导致MLSE不能获得最优的结果。针对MLSE时延和复杂度较高的问题，这里描述了一种基于Chase算法的滑动窗搜索时域均衡，有如下特点：

(1)Chase均衡采用的是树状搜索而不是栅格搜索；

(2)采用传统的自适应均衡器消除搜索中可能性小的幸存路径，同时估计信道参数；

(3)用滑动窗搜索的方法解决复杂度呈指数增长的问题。对小范围全部搜索，而不是对全局穷举；

(4)滑动窗搜索后逐比特的判决，而不是对符号序列进行估计，解决了译码时延的问题。

Chase均衡器由3部分组成，包括一个自适应均衡器和一个带滑动窗搜索的Chase算法以及一个信道估计器，如图1所示。

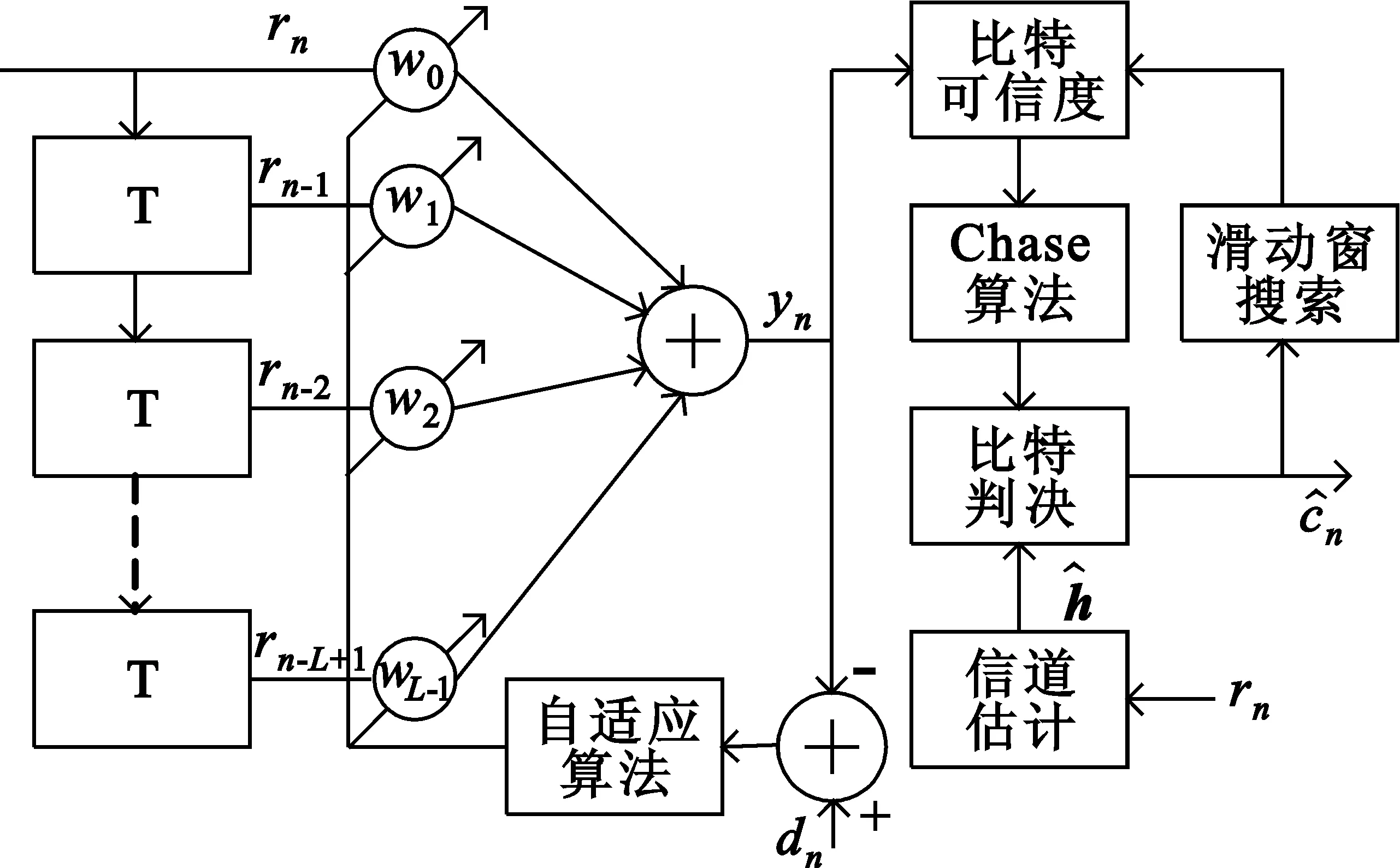
图1 Chase均衡器结构Fig.1 Chase equalizer structure

其中，自适应均衡器通过跟踪算法自适应地调整信道参数。传统的信道跟踪算法有最小均方误差(Least Mean Square，LMS)算法和递归最小二乘(Recursive Least Square，RLS)算法，前者结构简单，后者收敛速度快。

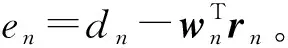
LMS算法是基于最小均方误差准则(Minimum Mean-squared Error，MMSE)的维纳滤波器和最陡下降法提出的。迭代公式为

wn+1=wn+2μ·en·rn

(6)

式中，μ是迭代步长。

RLS算法采用最小二乘准则，即在每一时刻对所有输入信号的加权平方误差和求最小化。同时引入遗忘因子λ，以达到更快收敛，其递推式为

wn+1=wn+kn·en

(7)

其中定义了信号自相关矩阵Rn和卡尔曼增益向量：

(8)

(9)

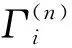
(10)

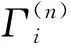
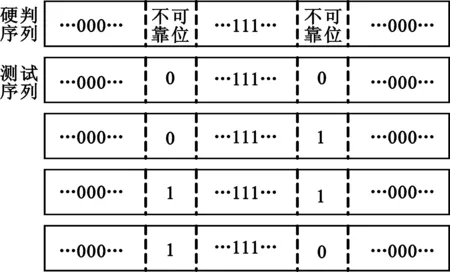
图2 构造测试序列Fig.2 Constructing test sequences

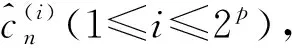
(11)

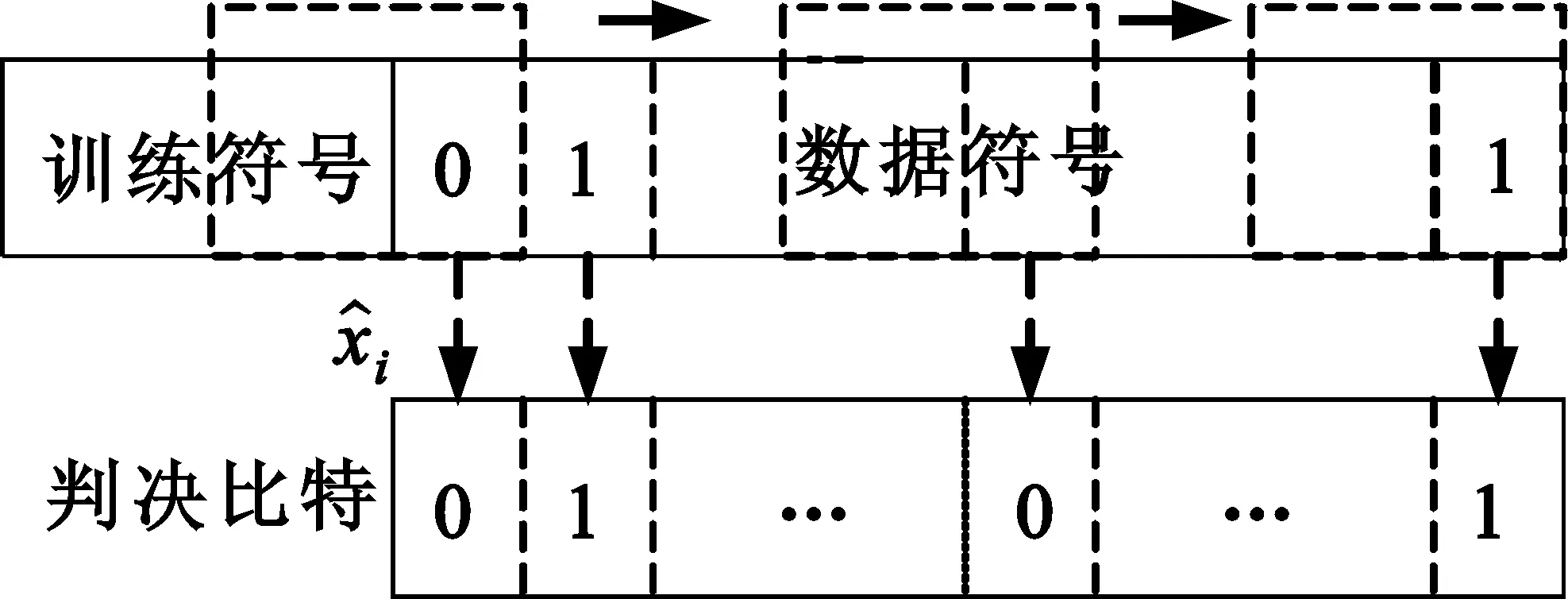
图3 滑动窗搜索过程Fig.3 The sliding window search

虽然前一比特判决的结果会用于下一比特判决中，但是利用了不可靠位构造测试序列，实现小范围内的穷搜索，消除了错误传输。

5 性能分析

5.1 BER性能

假设采用BPSK调制，由于nk是零均值的高斯白噪声，故当发送“0”时，均衡器输出yn的概率密度函数为

(12)

而当发送“1”时，yn的概率密度函数为

(13)

与它们相应的曲线如图4所示。

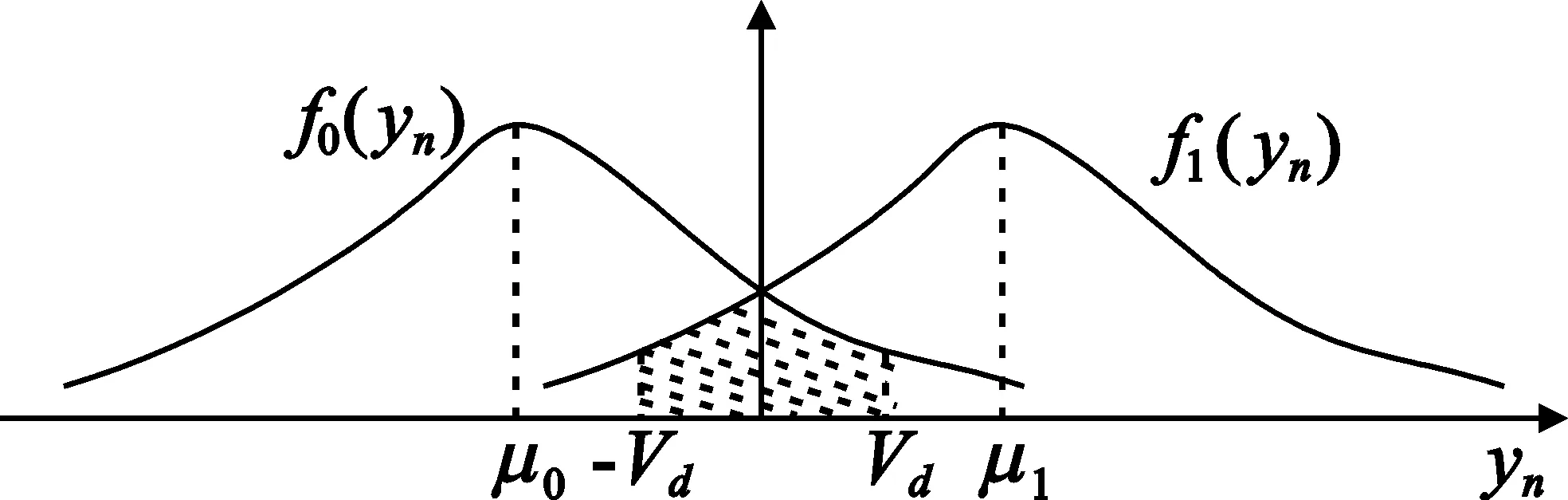
图4 yn的概率密度Fig.4 The probability density function(PDF) of yn

根据全概率公式，总的误码率可以表示为

Pe=P(0)P(10)+P(1)P(01)

(14)

假设BPSK调制输入等概，则上式可写成：

Pe=P(01)=

P(01,yn<-Vd)P(yn<-Vd1)+

P(01,-Vd≤yn≤Vd)P(-Vd≤yn≤Vd1)+

P(01,yn>Vd)P(yn>Vd1)

(15)

由门限判决可知：

(16)

并且设PChase=P(01,-Vd≤yn≤Vd)，故Pe可化简为

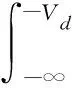
(17)

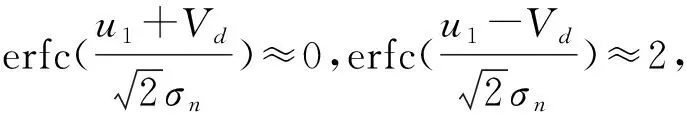
Pe≈PML，Vd→∞

(18)

5.2 复杂度分析

Chase均衡的复杂度主要取决于测试序列集合的大小。设均衡器输出yn在门限Vd内的概率为PV，则：

PV=P(-Vd≤yn≤Vd1)P(1)+

P(-Vd≤yn≤Vd0)P(0)

(19)

由于输入等概，可化简为

PV=P(-Vd≤yn≤Vd1)=

(20)

那么测试序列集合的大小为

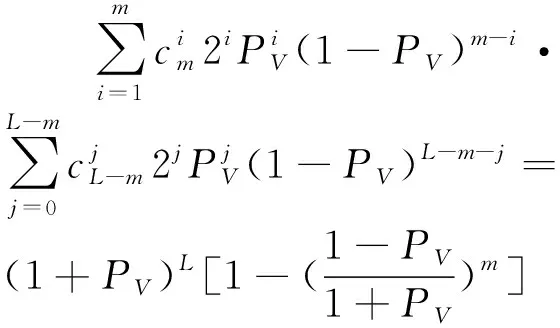
(21)

在BPSK条件下：

ψ2=2PV(1+PV)L-1

(22)

从表1中可以看出，L越大，Chase均衡的路径搜索就越小于MLSE，计算量也就越小。

表1 Chase均衡和MLSE的性能比较Table 1 Performance comparison between Chase equalization and MLSE

6 仿真结果

考虑BPSK调制，采用信道长度L=11的离散时间信道[3]，其冲激响应为[0.04 -0.05 0.07 -0.21 -0.5 0.72 0.36 0 0.21 0.03 0.07]，并且自适应均衡器长度与信道长度相同。设定信源发送的数据包含有500个符号，由100个训练符号和400个数据符号组成。

图5是当信道未知时的BER性能。此时，信道参数是通过训练序列估计得到的。在RLS自适应算法下Chase均衡性能优于LMS算法，这是因为RLS的收敛速度明显比LMS的收敛速度快。

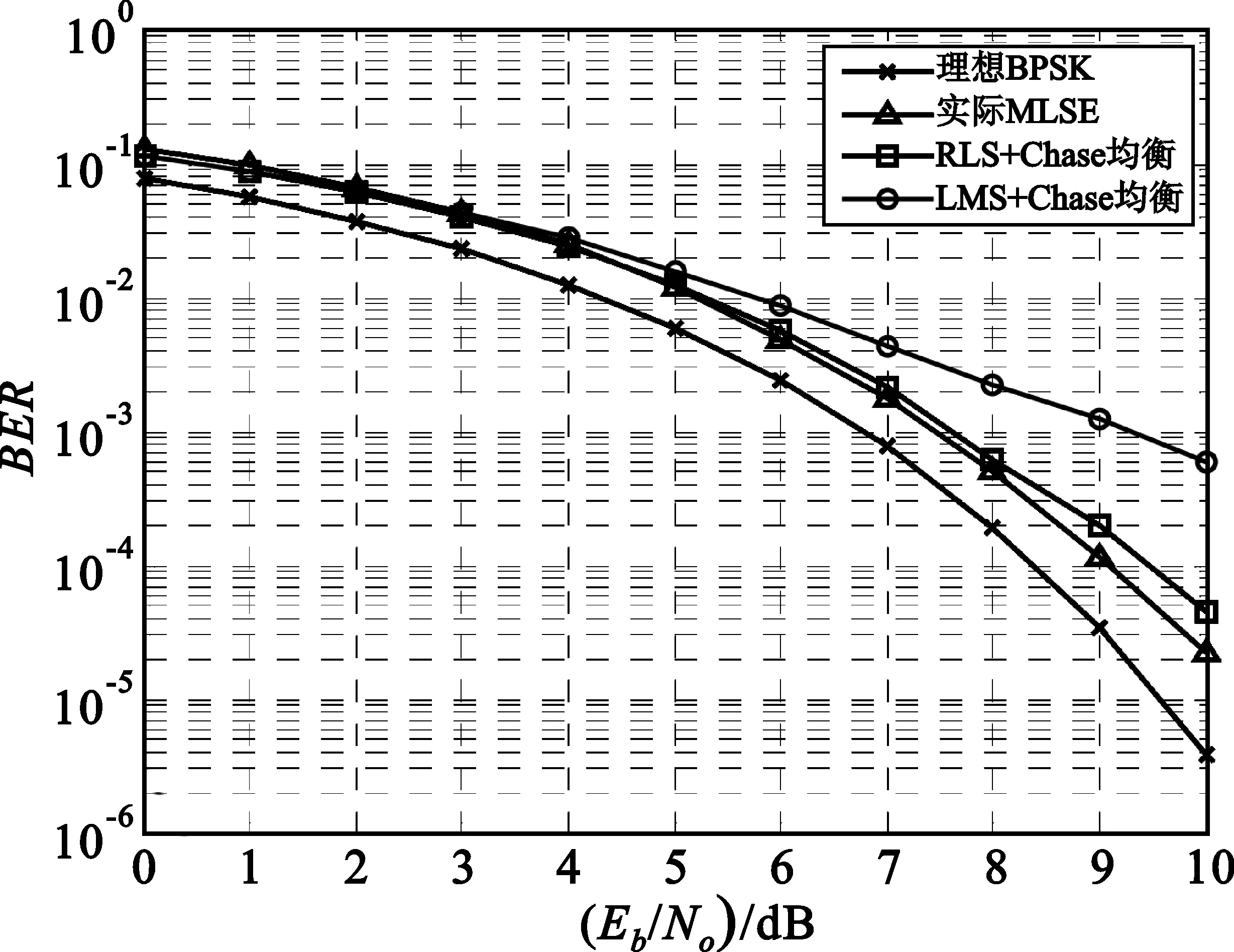
图5 信道未知时的均衡性能Fig.5 BER performance of the unknown channel

图6是可信度门限Vd对Chase均衡BER性能影响的比较。Vd增大计算量随之增大，但误码率下降并形成一个误码平层，因此必须找到一个合适的Vd达到计算量和误码率的折衷。

图6 可信度门限Vd与BER的关系Fig.6 The relationship between Vd and BER

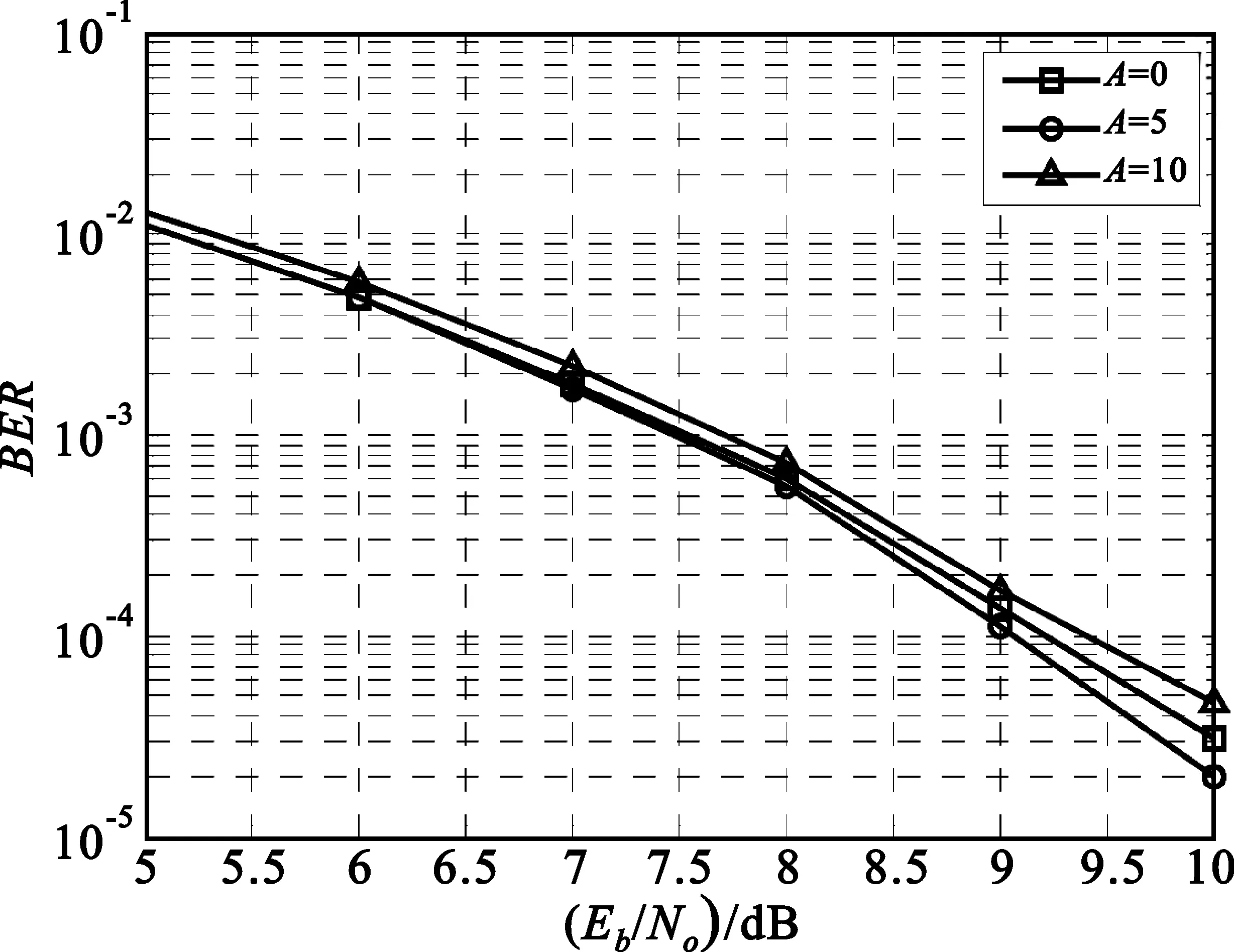
图7 比特判决的位置A与BER的关系Fig.7 The relationship between decision time A and BER

7 结 论

本文研究了一种基于Chase算法的低复杂度时域均衡方法。在信道未知情况下，自适应均衡器的输出作为软值进行可信度的计算，通过判决门限找到滑动窗内的不可靠位，并结合信道估计判决输出与接收序列欧氏距离最小的测试序列，由此消除了不可靠的搜索路径，减小了搜索长度，降低了计算复杂度，同时还保持了与MLSE非常接近的BER性能。理论分析和仿真实验表明， Chase均衡计算复杂度明显低于MLSE，而性能损失却很少。需要指出的是，RLS自适应算法是以复杂度为代价换取性能的提升。因此，如何设计更有效的自适应算法，进一步改善计算复杂度，仍需要进一步分析和研究。

参考文献：

[1] Forney G D. Maximum likelihood sequence estimation of digital sequences in the presence of intersymbol interference[J]. IEEE Transactions on Information Theory,1972,3(18):363-378.

[2] John G Proakis.Digital Communications[M].4th ed. Bei jing:Publishing House of Electronics Industry,2005:598-632.

[3] Myburgh H C,Olivier J C. Near-Optimal Low Complexity MLSE Equalization [C]//Proceedings of Wireless Communications and Networking Conference. Las Vegas:IEEE,2008:226-230.

[4] Myburgh H C,Linde L P. Reduced Complexity Combined Soft-Decision MLSE Equalization and Decoding [C] //Proceedings of Australasian Telecommunication Networks and Applications Conference. Adelaide: IEEE,2008: 209-213.

[5] Rubsamen M, Winzer P J,Essiambre R J. Simple method for MLSE performance estimation[C]//Proceedings of IEEE/LEOS Summer Topical Meetings. Portland:IEEE,2007:61-62.

[6] Luo Jie. Fast maximum likelihood sequence detection over vector intersymbol interference channels[C]//Proceedings of IEEE International Conference on Acoustics Speech and Signal Processing. Honolulu:IEEE,2007:465-468.

[7] Barhumi I，Moonen M. MLSE and MAP Equalization for Transmission Over Doubly Selective Channels[J]. IEEE Transactions on Vehicular Technology,2009,58(8):4120-4128.

[8] Patwary M N,Rapajic P B. Decision Feedback Persurvivor Processing: New Reduced Complexity Adaptive MLSE Receiver[C]//Proceedings of Asia-Pacific Conference on Communications. Perth:IEEE,2005:802-806.

[9] Zhou Hanbing,Li Daoben. A Simplified Kalman-MLSD Receiver over Fast Fading Channel[C]//Proceedings of International Conference on Wireless,Mobile and Multimedia Networks. Hangzhou:IEEE,2006:1-4.

[10] Liu T,Gazor S. Adaptive MLSD receiver employing noise correlation[J]. IEEE Proceedings of Communication, 2006,153(5):719-724.

[11] Ricklin N,Zeidler J R. Block Detection of Multiple Symbol DPSK in a Statistically Unknown Time-Varying Channel[C]//Proceedings of IEEE International Conference on Communications. Dresden: IEEE,2009:1-5.

[12] Jalden J,Ottersten B. On the complexity of sphere decoding in digital communications[J]. IEEE Transactions on Signal Processing,2005,53(4):1474-1484.

[13] Loskot P,Beaulieu N C. Sample Rejection for Efficient Simulation of Intersymbol Interference Channels with MLSD[C]//Proceedings of Wireless Communications and Networking Conference.New Orleans,LA,USA:IEEE,2005:911-916.