混合进化策略算法及其在函数优化中的应用

张成，李明辉(沈阳化工大学数理系，辽宁沈阳110142)

混合进化策略算法及其在函数优化中的应用

张成，李明辉
(沈阳化工大学数理系，辽宁沈阳110142)

自适应进化策略中高斯变异算子容易使进化过程陷入局部最优，出现进化早熟.文中针对上述缺点，引入柯西变异算子和子代距离率方法.在进化前期采用柯西的变异，保证个体能够快速地向全局最优的方向移动;在进化后期采用高斯变异，当个体聚集在全局最优解附近时，以较小的变异步长驱动个体向全局最优解方向移动.子代距离率系数进行调整变异算子.通过对单峰与多峰函数仿真试验，验证了算法的有效性.

函数优化;进化算法;进化策略;自适应步长

函数优化是智能算法应用中的一个基本问题.进化算法是基于自然选择原理的一种自适应搜索算法，是生命科学与工程科学的交叉学科，也是计算机科学和系统优化领域的热点研究课题.进化算法是现代科学计算的一种强有力方法，具有智能性、通用性和全局搜索能力，已成为函数优化问题的重要工具.它包括遗传算法、遗传规划、进化策略和进化规划.

达尔文的自然选择学说说明地球上的生物具有较强的繁殖能力，生物都是经过长期进化而不断完善自身的.大多数生物在繁殖过程中通过遗传使物种保持相似的后代;而部分生物由于变异，后代具有明显差异甚至形成新的物种.自然界中的生物根据优胜劣汰的原则不断地进行进化.进化策略算法是模拟生物进化而产生的一种进化算法，该方法在工程与控制领域有着重要的应用.

1 进化策略

进化策略由Rechenberg和Schwefel提出，是一种反映自然进化机制的随机优化技术.其搜索过程不依赖目标函数的梯度信息，具有较强的鲁棒性［1］.大量的研究表明［2］，进化计算方法在求解一些复杂的问题时，效果通常优于传统的优化算法.进化策略采用实数编码，适用于求解实值函数优化问题.进化策略算法按照其发展过程可划分为以下几种形式: (μ+1)，(μ+λ)，(μ，λ).本文采用(μ+λ)型，即父代种群由μ个个体组成，经过重组，突变产生λ个体，在μ+λ个体中进行进化策略的选择操作，最终生成下一代个体.

进化策略的工作步骤是:

(1)确定问题的表达方式.

(2)随机生成初始种群，并计算适应度.

(3)根据进化策略，用下述操作产生新的群体.

①重组.将两个父代个体交换目标变量和随机因子产生新的个体.②变异.对重组后的个体添加随机变量产生新的个体.③计算新的个体的适应度.④选择.根据选择策略，挑选优良个体组成下一代群体.

(4)反复执行(3)，直到达到终止条件，选择最佳个体作为进化策略结果.

n维实值函数f:S→R，SRn，sj∈［aj，bj］，j= 1，2，…，n.寻找一点Xmin∈，使f(x)最小，即X∈S，f(Xmin)f(X).Backend schaefer提出的自适应进化策略算法(SAEP)，采用公式(1)对个体进行突变操作

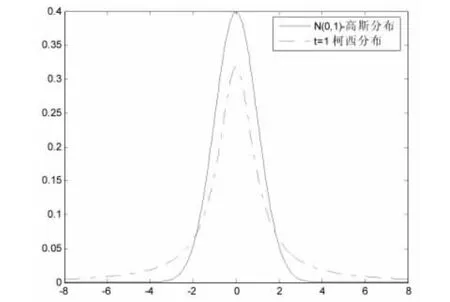
图1 高斯分布与柯西分析比较

2 进化策略算法变异算子的改进

在进化策略中，变异算子作为主要算子起着相当大的作用.所以进化策略的收敛速度与变异有着密切的关系.为了改变现有进化策略在收敛性能方面存在的不足，这里主要从变异这一方面进行改进.因此，在原来变异算子的基础上提出一种新的变异算子，即柯西变异算子.

Caucy(1)和Caucyj(1)均为一个柯西分布的随机数，它比高斯分布产生的随机变量的范围大，同时对目标变量(xij(t))和策略变量(ηij(t))进行修改.称公式(2)为柯西变异算子(Caucy)［5］.根据两种分布的特点，提出改进的混合变异进化策略算法.在进化初期引用柯西变异算子，在进化后期引用高斯变异算子.这样可以在初期应用柯西随机数产生较大的变异步长，使群体中个体能够快速向全局最优解移动，以提高收敛速度，避免出现早熟问题.同时，在进化后期采用高斯变异，可以保证当前代中最优个体稳步向全局最优解方向移动，提高收敛精度.

对于变异算子的选择引入子代距离率pdistance(t).第t子代距离率由下式计算:

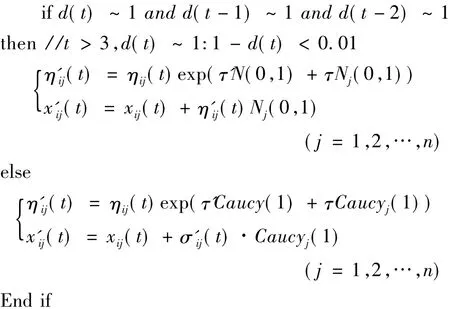
3 仿真试验

测试函数1:De Jong函数min f=i∈［－512，512］.这是一个典型的多元单峰函数，二维(n=2)图形如图2所示，该函数的最小值出现在坐标原点，最小值为0.

图2 De Jong函数2维图像

设种群规模为N=50，维数为n=20，随机生成初始种群P(0)，进化代数gen=200独立运行10次.下面将高斯变异(SAEP)、柯西变异(CEA)、本文算法(GCEA)及遗传算法(GA)四种测试结果进行以比分析.同时图3、图4给出种群初始化及200代种群均值与最优解的变化趋势图.

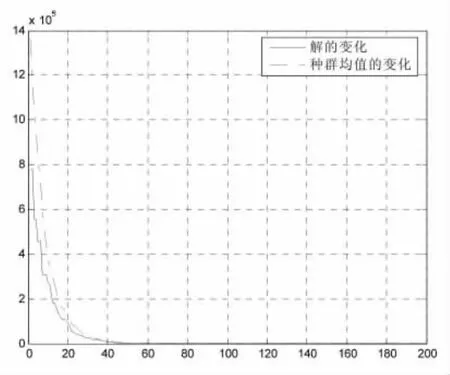
图3 混合变异解与均值变化

表1 算法仿真试验对比表

图4 种群初始化目标函数散点图

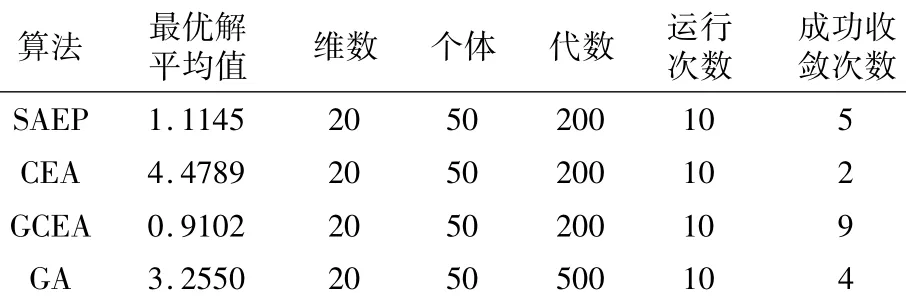
表2 四种算法运行10次最优解均值分布情况

表1表明本文算法可以在相同条件下使收敛精度高于其它算法.由图3可以看出本文算法在进化初期能够提高进化速度，使种群中的个体能够快速、稳定地向全局最优解的方向移动.而在进化后期可以保证个体在全局最优解附近波动，提高收敛精度.图4说明在进化初期种群分布范围较广，能够搜索范围比较完整，能够有效在全局进行搜索.表2说明混合变异算法在运行上比较稳定且平均收敛程度要高于遗传算法.

测试函数2:Shubert函数是一个典型多元多峰值的函数.

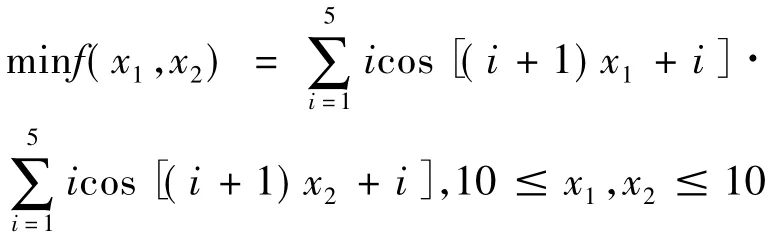
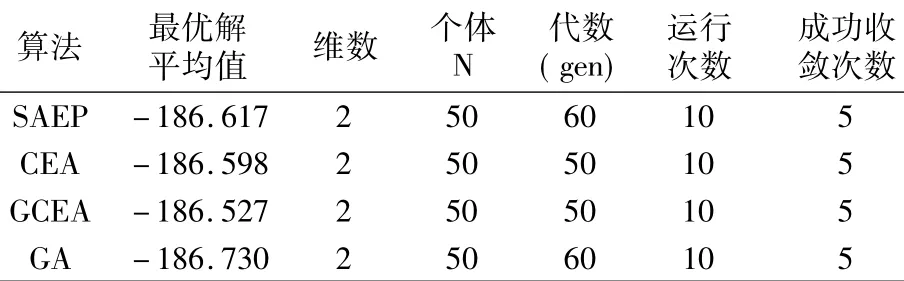
表3 各种算法运行10次最优解均值分布情况

表3中数据说明本文算法对于多峰极值问题是有效的.在同维数(2维)、同个体(50个)前提下本文算法通过较少进化代数即可以取得优化结果.对于精度要求较高的优化问题，本文算法也能达到理想的收敛效果.

［1］周明，孙树栋.遗传算法原理及应用［M］.北京国防工业出版社，1999.

［2］Kim JH.MYUNG H.Evolutionary programming techniques for constrained op tmfization problems［J］.IEEE Transactions on Evolutionary Computation 1997，1(2):129－140.

［3］X.Yao，Yule，Glen.Evolutionary Programmingmade faster［J］.IEEE Trans.Evolutionary Computation，1999，3(2):82－102.

［4］T.Back，H－P，Schaefer.An overview of evolutionary algorithms for parameter optimization［J］.Evolutionary Computation，1993(11):1－23.

［5］王战全，云庆夏，等.进化策略中变异算子的改进研究［J］.计算机仿真，1999(7):16－3.

［6］雷英杰，等.MATLAB遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005:111－115.

(责任编辑:王前)

Abstract:In adaptive evolution strategy，Gaussianmutation operatormade the evolutionary process fall into local optimal，the evolution appeared premature.Aiming at the shortcoming，introducing Cauchymutation operator and progeny distance ratemethod.In the early evolution，using the variation of Cauchy，ensure the individual can quicklymove to global optimal direction.In the later evolution using Gaussian mutation，when the individual gathered in the vicinity of global optimum solution，with smallermutation step drive the individual tomove to global optimal solution direction.Through the single－peak and multi－peak functions，a simulation testing verifies the effectiveness of this algorithm.

Key words:function optimization;evolutionary algorithm;evolutionary strategy;self－adaptive step

Hybrid Evolutionary Strategy Algorithm and Its Application in Function Optim ization

ZHANG Cheng，LIMing－hui
(Shenyang University of Chemical Technology，Shenyang，Liaoning 110004，China)

TP301.6

A

1008－7974(2011)04－0028－03

2010－10－20

张成(1979－)，男，辽宁锦州人，硕士，沈阳化工大学数理系讲师.