基于小波能量熵和支持向量机的高压输电线路故障选相方法研究

张明光 陆文辉 刘昱晨（兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050）

0 引言

随着我国现代电力系统规模的日益扩大，输电容量和电压等级的不断提高，当高压输电线路发生故障后，迅速准确地得知故障相别，对于保证其继电保护装置的正确动作、有选择地切除故障具有重要意义。特别是近年来受到广泛关注的新型行波保护和暂态保护更离不开快速可靠的故障选相［1－2］。同时，故障选相也是实现精确故障定位的重要前提。

输电线路故障选相过程主要包括故障特征信息的提取和状态识别2个部分。近年来，新兴的数学工具及数字信号处理技术在故障选相的方法研究上获得了广泛的应用。如文献［3］引进数学形态学来实现故障特征分量的处理。文献［4］基于分形理论实现对输电线路故障分类。文献［5］将固有模态能量熵应用于高压输电线路的故障特征信息的提取。总体来说，这些新的选相方法适应于系统更多工况的特点，克服了传统方法的一些不足。但大多还仅仅建立在理论分析与仿真的基础上，实践运行上还不够成熟。近年来多种信息熵理论［6］和小波的结合越来越多地用于故障特征信息的提取中，如小波熵、小波时频熵、小波包能量熵、小波奇异熵等［7］。由于小波熵结合了小波时频分析的独特优势和信息熵对信号复杂程度的统计特性，各种小波熵理论已经在故障选相中取得了较好的应用。本文应用Shannon信息熵的概念，结合小波分析技术，定义适当的小波熵度，用以衡量信号的不确定性（即复杂度），可有效进行故障特征信息的提取。同时，利用目前解决小样本分类的最佳理论——支持向量机（SVM）来进行模式识别，SVM被公认为是人工神经网络的替代方法。用SVM分类器作为模式识别可以通过机器学习，准确得出数据内在的规律，实现准确分类。

本文在理论分析基础上，将信息熵理论与小波分析技术相结合，应用于高压输电线路的故障特征信息的提取，并利用最小二乘支持向量机（LS—SVM）分类器来实现故障类型的识别。该方法首先利用二进制离散小波变换对故障后三相电流信号进行分析，然后在一定的时间窗内计算每相的小波能量熵，从而得到三相电流信号的小波能量熵累加值以及比值，并将其作为反映故障信息的特征分量。最后将得到的故障特征信息分量输入LSSVM建立故障分类器，进一步判断输电线路故障类型。本文根据实际参数，利用MATLAB建立具体的输电线路仿真模型。最终仿真结果表明，该方法不受运行方式、系统振荡和短路过渡电阻的影响，能快速可靠地进行故障选相。

1 基本原理

1.1 小波变换及Mallat算法

设函数Ψ（t）∈L2（R），Ψ（ω）为其傅里叶变换，如果满足

则称Ψ（t）为一个基本小波。

设

称式（2）为母小波，其中:a为尺度因子;b为位移因子;a、b∈R，a≠0。

设函数f（t）∈L2（R），则其对应的连续小波变换为

对应的离散小波变换为

Mallat在图像的分解与重构的塔式算法的启发下，根据多分辨率理论提出了小波分解与重构的快速算法，即Mallat算法。

基本思想:设Hif为能量有限信号f∈L2（R）在分辨率 2j下的近似，则Hif可以再分解为f在分辨率2j－1下的近似Hi－1f（通过低通滤波器得到）以及位于分辨率2j－1与2j之间的细节Di－1f（通过高通滤波器得到）之和。分解过程如图1所示。

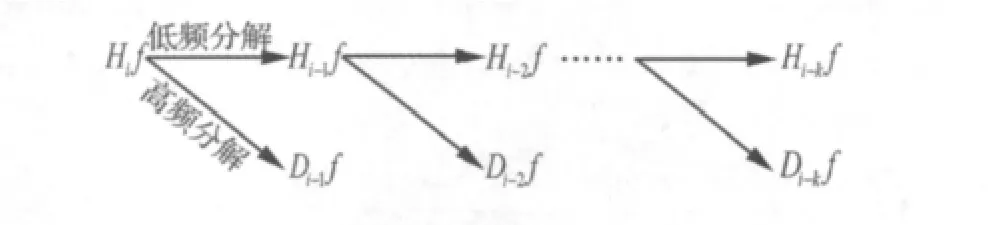
图1 Mallta算法分解过程示意图

1.2 小波能量熵及故障特征分量提取

当高压输电线路发生故障时，其故障信号的幅值和频率都会发生很大变化。根据熵的原理，可以通过定义熵的测度来衡定信号的复杂性。本文利用的是由文献［8］定义的小波能量熵

设E=E1，E2，…，Em为信号x（n）在m个尺度上的小波能谱，则在尺度域上E可形成对信号能量的一种划分。由正交小波变换的特性可知，在某一时间窗（窗宽为L∈N）信号总功率E等于各分量功率Ej之和。设pj=Ej/E，则∑jpj=1，于是定义相应的小波能量熵（wavelet energy entropy，WEE）为

本文将电流暂态信号作为采集信号，式（5）定义的小波能量熵反映了电流频率（尺度）空间的能量分布信息。

可以看出，当信号经过小波分解后，非故障中高频分量小、基频分量大，使得计算出的小波能量熵很小;而故障相中除基频分量外，高频分量变大，使得小波能量熵变大。

本文首先得出数据窗口内的三相电流信号小波能量熵累

计值

根据理论分析，输电线路故发生故障时，式（6）、式（7）中的6个量包含了能够反映故障特征的信息。因此，也一定能够作为故障选相的判断依据。同时，让这六个故障特征分量作为之后分类机的输入数据（信号），以便分类机最终能够精确可靠的完成输电线路的故障选相。

为了提高选相的可靠性，进一步的反映故障相和非故障相的准确差异，再引进三相电流的小波能量熵比值:

1.3 最小二乘多分类支持向量机

最小二乘支持向量机（LS－SVM）算法可表示为如下优化问题

上式中x是输入矢量，ω是可调的权值矢量，b是偏执，ξ≥0为松弛变量，可以度量一个数据点对模式可分的理想条件下的偏离程度，γ是平衡最小分类边界和最小分类误差的惩罚因子，非线性变换变换φ（x）将给定输入样本x映射到更高维的特征空间。由式（8）可以看出，与一般SVM不同，LS－SVM使用的是等式约束条件。式（8）优化问题对应的Lagrange方程为

式中ai为Lagrange乘子。此优化方程的求解等价于

通过求解方程组式（9），并消去 ω和ξ，可以得到以下线性方程组

其中，

求解线性方程组式（10）可得a和b，则LS－SVM分类决策函数为

式中k（ ）为满足Mercer定理的核函数［9］.本文采用的是线性核函数

LS－SVM是一种两类分类器，而实际输电线路对应着1种正常运行状态以及10种短路故障状态。本文采用SuYken等［10］提出的多类LS－SVM法，即对于k类样本，采用k－1个LSSVM进行逐层分类。逐层分类法分类速度较快，不存在分类盲区，是一种非常适合模式识别的SVM多类算法。如图2所示，建立一个可以分离10种故障的多级分类器，实现故障类型的判别。

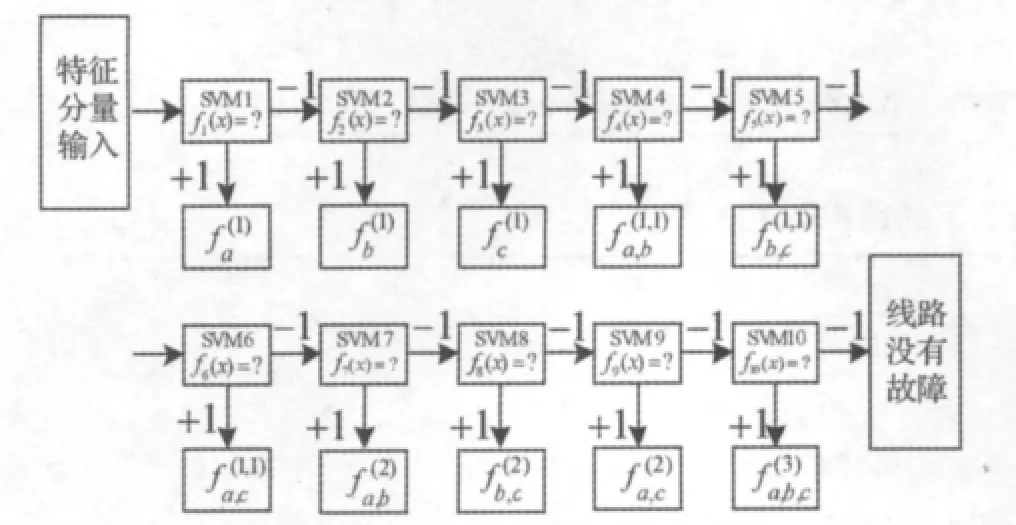
图2 支持向量机短路故障分类器

2 基于WEE和LS－SVM的输电线路故障选相方法

基于WEE和LS－SVM的输电线路故障分类及选相方法流程如图3所示。

图3 输电线路故障选相流程图

本文采用的仿真系统模型是一典型的500 KV双端供电输电系统，如图4所示。

该线路模型总长220 km，在工频情况下正序参

数为r1=0.016 Ω/km，x1=0.299 Ω/km，b1=4.314 μs/km;零序参数为r0=0.286 Ω/km，x0=1.421 Ω/km，b0=2.497 μs/km。

以三相电流为研究对象，采用200 kHz采样频率、db5小波和基于Mallat算法，分解层次定为m=5。同时分别对不同的过渡电阻、故障位置以及故障初始角的各种短路故障进行了大量仿真。

图5为线路AB距A侧110 km处发生A相经50 Ω过渡电阻单相接地故障时的三相电流波形。同时将A相电流进行小波变换分析，如图6所示。

发生故障时，对三相电流信号按上述方法处理后，就能够得到小波能量熵累计值以及比值，从而构成支持向量机的输入向量T=［TA，TB，TC］。例如对于A相，处理后得到TA=［Sa，Rab］。同理，对于B相、C相得出TB、TC。表1为线路故障三相电流信号的小波能量熵累加值以及比值。当发生AB相间短路时，所求出的A相、B相的Sa和Sb明显大于C相的Sc。同时可以看出Rab的值比较低，而Rbc和Rac的值很高。分析表明，发生不同的故障时，各相小波能量熵累计值以及比值都不同，故将其作为故障特征向量完成故障选相是可行的。

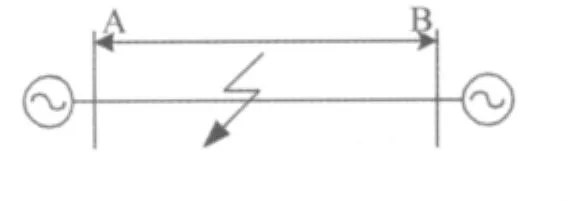
图4 双端输电线路仿真系统模型

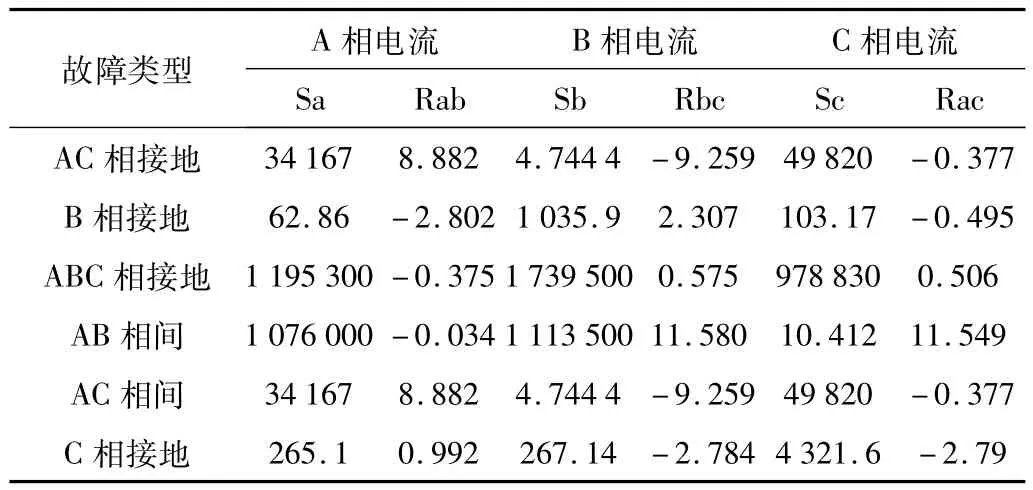
表1 三相电流信号的小波能量熵累加值以及比值

输电线路短路故障基本有10种故障类型。本文对线路全长98%范围内的不同距离位置、不同的过渡电阻以及故障初始角不同情况的下进行大量各种短路故障仿真实验，得到故障样本100组，并从中取出50组数据作为LS－SVM的训练样本，将剩下的50组数据作为测试样本。表2－4给出的是不同故障情况下的的识别结果。可以看出，利用LS－SVM来完成故障选相的准确率为100%，也就说明了此故障类型识别方法不受系统运行方式、过渡电阻以及故障位置的影响，具有较强的通用性和实用性。

表2 不同过渡电阻情况下的选相结果

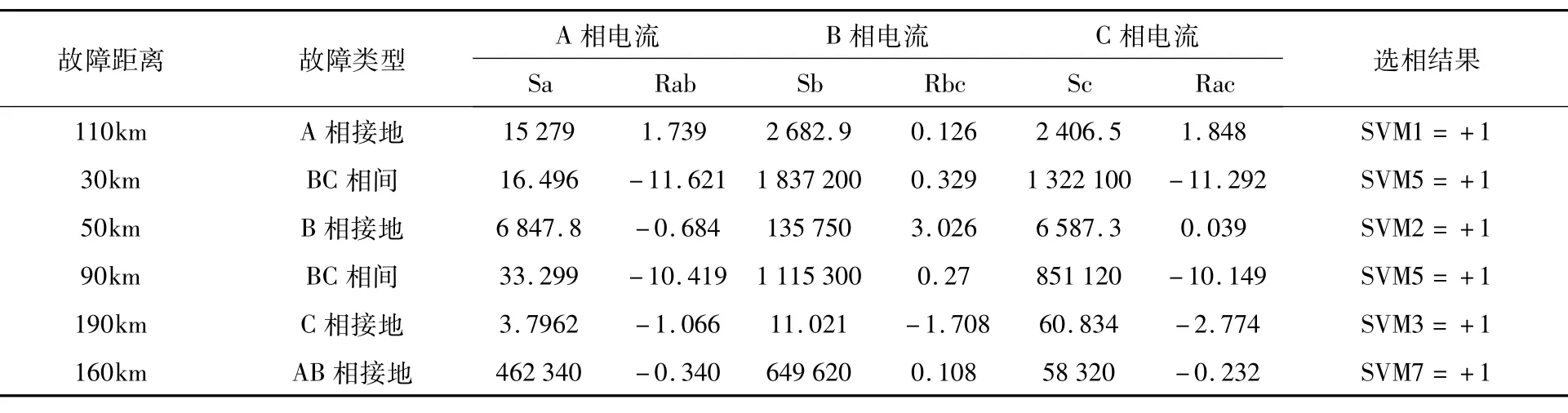
表3 不同故障距离情况下的选相结果

表4 不同故障初始角情况下的选相结果

3 结束语

本文提出了一种基于小波能量熵和最小二乘支持向量机（LS－SVM）的高压输电线路故障选相的新方法。信息熵理论和小波分析技术相结合定义的小波能量熵概念，能够准确提取不同的故障特征信息，并在此基础上利用最小二乘支持向量机算法来实现线路的故障选相。该方法不受系统运行方式、过渡电阻、故障位置以及故障初始角因素的影响，能够有效地识别故障类型，具有较强的通用性和实用性。

［1］王亚强，焦彦军，张延东.（超）高压输电线路故障选相现状及其发展［J］.继电器，2004，（24）:72 －77，85.

［2］ Cheng Jing-zhou，Zhang Ju.Novel Technique for Fault Phase Selection Based on Correlation Analysis and Fuzzy Set Using the Transient Signals in EHV Power System［J］.Automation of Electric power systems，2005，29（5）:50－55.

［3］邹力，赵青春，林湘宁，等.基于数学形态学的电力系统振荡中故障识别和改进的选相方法［J］.中国电机工程学报，2006，26（13）:37－42.

［4］杨丹，刘柿，王冬青，等.基于分形理论的输电线路故障检测和选相［J］.电力系统自动化，2005，20（15）:35 －39，88.

［5］李晓晨.基于数据挖掘技术的高压输电线路故障选相方法［D］.东北电力大学电气工程学院.2008.

［6］何正友，蔡玉梅，钱清泉.小波熵理论及其在电力系统故障检测中的应用研究［J］.中国电机工程学报，2005，25（5）:40 －45.

［7］何正友，符玲，麦瑞坤，等.小波奇异熵及其在高压输电线路故障选相中的应用［J］.中国工程电机学报，2007，27（1）:31 －36.

［8］张斌，何正友，钱清泉.基于小波能量熵和模糊逻辑的故障选相元件［J］.电网技术，2006，15（8）:30 －35.

［9］邓乃扬，田英杰著.支持向量机:理论、算法与拓展［M］.北京，科学出版社.

［10］ Su Yken J A K， Branbanter J D， Luka S L， et al.［J］.Neurocomputing，2002，48（1）:85－105.