EG M2008模型精化研究及其在濒海工程中的应用

2011-09-19冯义楷刘焱雄

测绘通报 2011年2期

关键词：精化水准面合法

冯义楷,刘焱雄 ,彭琳,于甲,李杰

(国家海洋局第一海洋研究所,山东青岛 266061)

EG M2008模型精化研究及其在濒海工程中的应用

冯义楷,刘焱雄 ,彭琳,于甲,李杰

(国家海洋局第一海洋研究所,山东青岛 266061)

利用最新的全球大地水准面模型 EG M2008,结合区域 GPS/水准网点成果精化区域大地水准面模型,并将该模型的计算结果分别与 GPS/水准网点直接内插所得结果、实测数据所得高程异常值进行对比。结果显示,我国大地水准面与全球大地水准面之间存在系统性偏差,约为 24.5 cm;在沿海地区精化的区域大地水准面模型可达到 ±5 cm的精度,可以满足近岸海岛高程传递和近岸海洋测绘等工作的需要。

EG M2008模型;高程异常;大地水准面;移去-恢复

一、引言

近海海洋工程及岛礁水深地形测量中,经过潮汐改正后,需要将水深资料最终归算到验潮站的理论深度基准面。理论深度基准面与 1985国家高程系统存在对应关系,因此,需要精确确定验潮站的1985国家高程 (正常高)。由于我国近海岸地区水准点稀少,近岸工作区获取精确水准点资料非常困难;海岛远离陆地,不可能采用水准测量方式传递高程,如何进行海岛高程传递一直是海洋测绘中的难点问题。海岛高程基准传递的方法有静力水准法、动力水准法、GPS水准法及常规大地测量法等四种方法。已有专家对静力水准法、动力水准法及常规大地测量法等三种方法的优缺点作了详尽分析[1]。目前,国家测绘局和国家海洋局都在组织开展海岛礁测绘工作,其目的是获取海陆统一的陆地和海域地形图。因此,如何快速、准确及有效地确定验潮点 1985国家高程及近海海岛高程传递成为研究人员当前急需解决的技术难题。

2008年,美国国家地理空间情报局发表了其最新研制成果——EG M2008模型。EG M2008模型与早期出现的模型相比,模型更复杂、精度更高,将全球高程异常精度提高了 3～5倍。章传银、郭春喜等对 EG M2008模型在中国内地的适用性进行了研究,结果显示 EG M2008模型计算的高程异常在我国大陆的总体精度为 20 cm,在东部沿海地区精度约10 cm[2]。因此,完全可以利用沿海地区现有 GPS资料结合 EG M2008模型在濒海地区实现高精度的高程传递,满足海洋工程测量的需要。

二、EGM 2008模型及精度

EG M2008模型采用的基本格网分辨率为 5′×5′,数据主要来自地面重力、卫星测高及卫星重力等测量。在计算时 EG M2008模型采用 ITG-GRACE03S模型作为先验误差协方差矩阵,将 GRACE数据作为计算 EG M2008地球重力场低阶位系数的主要数据源,EG M2008模型在精度及分辨率方面都取得了巨大的进步。表 1为 EG M2008模型与现有其他模型高程异常值精度统计,结果显示 EG M2008模型与其他模型相比具有较高的精度。

表 1 各地球重力场模型 GPS水准外部检核结果均方差

三、数据处理方法

1.移去-恢复方法

GPS水准点高程异常ξ的计算公式为

式中,h为 GPS测量的大地高;H为由水准测量得到的正常高。

为实现 GPS测量点的大地高向正常高转换,准确计算测量点高程异常ξ是关键。ξ可表示为

式中,ξM是由地球重力场模型计算的模型高程异常,对应高程异常中的中、长波部分;Δ ξ为高程异常残差。

在高程异常变化较大区域,直接根据离散点的高程异常通过数值拟合内插确定待定点高程异常,会出现较大误差。可先由 GPS/水准点实测高程异常ξ减去模型计算的高程异常值ξM,获得平滑度较高的残差高程异常场,然后由此残差场拟合出待定点残差高程异常值Δ ξ。通过模型计算待定点的高程异常值ξM,将残差高程异常值与模型计算的值相加,即可得到待定点精确的高程异常值ξ,结合待定点 GPS实测大地高 h,可以获得待定点正高 H,此方法为移去-恢复法。该方法的优点是通过拟合内插平滑度较高的残差高程异常场来提高高程异常计算精度。

2.模型高程异常值计算

EG M2008模型高程异常计算公式为[3-4]

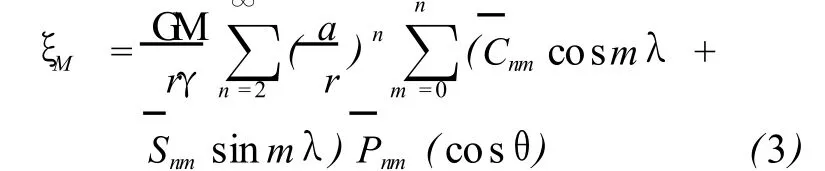
3.数据内插拟合

在移去-恢复技术中拟合高程异常残差场形成格网以及通过格网数据计算未知点的高程异常残差时,都需要用到拟合函数。因此,选择拟合函数合理与否对最后成果的精度也产生影响。常用的拟合方法有:等值线法、平面拟合法、二次曲面拟合法、多面函数法、三次样条曲线拟合法、多项式曲线拟合法、加权反距离拟合法。各函数对地形及区域有其自身的适用性,平面拟合法较适合于高程异常变化平缓的平原地区;二次曲面及多项式曲面拟合较适合于小区域;三次样条曲线、多项式曲线拟合则一般用于测量点呈直线排列的情形[5]。本文在数据处理时选择平面拟合法、二次曲面拟合法及加权反距离拟合法。

4.高程异常计算

近年来,国家测绘局和沿海省市在中国沿海布设了大量的 C级和 D级 GPS网点,并在这些网点上施测了部分水准。利用这些 C级和 D级 GPS控制网点的 GPS/水准资料与 EG M2008模型,通过移去-恢复技术计算出试验区域高程异常残差场;然后基于 EG M2008模型和残差场,可以计算出未知点位的正常高,也能按照格网要求,计算出格网点上的高程异常。

四、试验及成果分析

1.青岛试验结果

笔者共收集了青岛市 C级 GPS网控制点 60个,D级 GPS网控制点 5个,C级控制点均引测过二等水准,D级点为四等水准高程。将 C级 GPS控制点实测的高程异常值与模型计算的高程异常值比较,如表 2所示。

表 2 实测高程异常值与 EGM2008模型计算值之差结果 cm

结果显示,高程异常值之差全为正数,这说明我国大地水准面与全球大地水准面之间存在系统性误差。由于我国水准原点位于青岛市区,C级网控制点大概分布在水准原点周围。因此,可以将该地区高程异常值残差平均值作为我国 1985国家高程系统定义的似大地水准面与全球大地水准面之间的系统性偏差,由此得到我国似大地水准面与全球大地水准面之间存在系统性误差为 24.5 cm。为简化计算,将各 C级 GPS点位上的高程异常值之差减去系统性偏差,得到无系统偏差的高程异常残差。对残差数据利用平面拟合法、二次曲面拟合法、加权反距离拟合法等三种方法拟合后,得到格网化的高程异常残差曲面[6],如图 1所示。

根据格网点的高程异常残差及坐标值,内插出各检核点点位的高程异常残差值;然后,利用各检核点的大地高和 EG M2008模型计算的高程异常值,通过系统误差改正以及高程异常改正,联合解算出检核点的正常高 (或 1985高程)。

为便于比较,也可以直接利用 C级 GPS控制网的高程异常值进行曲面拟合,然后再内插出检核点位的正常高。在选择 D级点时,重点考虑靠近沿海的点。同时 C级网中 C049建设在海边,将 C049作为精度检核点。将 D级 GPS网控制点的实测高程异常值作为真值与两种方法计算的高程异常值求差,结果如表 3所示。

比较各差值的平均值及均方差,如表 4所示。

图 1 三种拟合残差曲面图

表 3 模型及直接拟合计算高程异常与实测高程异常比较结果 m

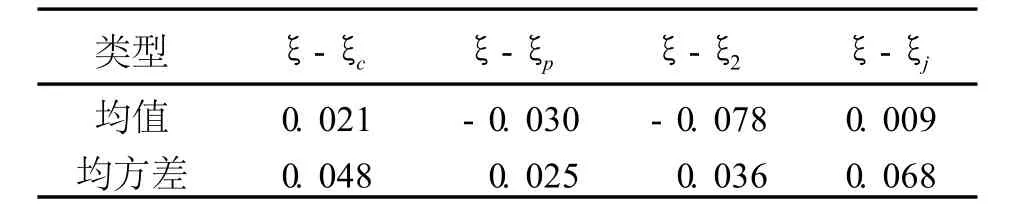
表 4 均值及均方差比较 m

通过表 3～表 4的结果显示,利用本文构建模型计算的高程异常值总体精度优于直接拟合内插出的高程异常。这表明,完全可以通过 EG M2008模型结合当地 GPS控制网计算出高精度的近岸及近岸海岛控制点水准高,可以满足验潮及作为图根控制点精度的要求;在残差模型拟合时,平面拟合与二次曲面拟合法计算的高程异常值精度高于加权反距离法计算的值。

2.广西茅尾海试验及结果

茅尾海位于钦州湾的顶部,是以钦江、茅岭江为主要入湾径流的河口海滨区,总面积约 135 km2,其中滩涂面积占总面积的 80%。该内湾内浅滩密布,潮沟众多,潮汐情况十分复杂。部分滩涂在高潮时测量船只也无法到达,在此种区域利用网络RTK进行测量,网络 RTK得到的高程数据为WGS-84坐标系的椭球高,在数据处理时需要将椭球高转换成 1985国家高程 (正常高)。

在高程数据转换过程中,笔者利用广西泛北部湾 GPSD级网WGS-84坐标和控制点上的二等水准高程值结合 EG M2008模型,按照上述方法进行了局域大地水准面精化,建立了钦州湾地区局部大地水准面精化模型,并通过模型实现 RTK测量值从椭球高到正常高的转换。在茅尾海周边有两个验潮站,其正常高是按四等水准要求引测的,通过精化水准面模型计算的验潮站的高程值与水准仪引测的高程值差值均在 5 cm内。RTK测量数据与测深仪测量值有部分重合,对重合点进行比较分析,发现重合点高差之差基本在 0～20 cm内,这完全满足水深测量在浅水区域限差在 30 cm以内的要求。这表明,通过区域精化大地水准面模型求得的高程精度完全满足海洋工程所需数据精度的要求。