非负矩阵分解在高光谱图像解混中的应用探讨

李二森，张保明，杨 娜，杨靖宇，郭晓刚

(信息工程大学测绘学院，河南郑州450052)

非负矩阵分解在高光谱图像解混中的应用探讨

李二森，张保明，杨 娜，杨靖宇，郭晓刚

(信息工程大学测绘学院，河南郑州450052)

从线性混合模型与非负矩阵分解的定义出发，分析非负矩阵分解适用于高光谱图像解混的原因，总结近年来学者们提出的基于非负矩阵分解的光谱解混算法，并重点对SC-NMF、MVC-NMF、APS-NMF算法步骤进行介绍与分析，最后总结非负矩阵分解及其应用于混合像元分解所面临的问题。

混合像元;光谱解混;非负矩阵分解;线性混合模型;端元

一、引 言

混合像元在高光谱图像中广泛存在，传统的硬分类方法可能会产生不准确的分类结果，而子像元分类方法能够提供更加精确的分类结果用于确定细小的特征。如何从混合像元广泛存在的高光谱遥感图像中准确地提取端元，并有效地对混合像元进行分解，已成为遥感图像定量分析的一个重要研究课题。

总的来说，混合像元分解模型可以分为两类，即线性光谱混合模型(linear spectral mixture model，LSMM)和非线性光谱混合模型(nonlinear spectral mixture model，NLSMM)。其中线性光谱混合模型的原理简单、效率高、物理意义明确，因而得到广泛的研究和应用。

非负限制下的低阶估计问题通常被称作非负矩阵分解(nonnegative matrix factorization，NMF)，NMF的思想可以追溯到1994年Paatero和Tapper的文章［1］。Lee和Seung在一篇关于非监督学习的文章［2］中也独立地提出了NMF的概念，随后他们发表在《自然》上的一篇文章给出了计算NMF的简化算法［3］，用于解决人脸识别和语义分析中的问题，而且他们以矩阵的欧氏距离和K-L散度作为目标函数，证明了NMF算法的收敛性。目前，NMF在人脸识别、数据挖掘、数据压缩、非负数据的解译、语音信号处理和神经生物学等领域中得到了广泛应用［4-5］。NMF的数学模型与线性光谱混合模型十分相似，为将NMF应用于线性混合模型下的光谱解混提供了可能。文献［6-7］将没有附加任何限制的NMF直接应用于光谱解混，在试验中取得了一定的成果，文献［8-10］结合非负矩阵分解分别提出了平滑限制非负矩阵分解(smoothness constrained nonnegative matrix factorization，SC-NMF)、最小体积限制的非负矩阵分解(minimum volume constraint nonnegative matrix factorization，MVC-NMF)和交互投影子梯度非负矩阵分解(alternating projected subgradients-nonnegative matrix factorization，APS-NMF)应用于高光谱混合像元解混，在试验中取得了较好的结果。

本文在分析线性光谱混合模型和NMF原理的基础上，对NMF在光谱解混中的应用进行了研究，并对MVC-NMF、APS-NMF和SC-NMF三种算法进行了总结，最后分析了NMF及其应用于光谱解混面临的问题。

二、线性光谱混合模型

线性光谱混合模型的表达式为

式中，x为l(l为影像波段数)维混合像元光谱，是已知观测量;A为l×p(p为端元数目)端元矩阵或源矩阵，其中每一列为一个端元的光谱向量;向量s为该像元中各端元的丰度(abundance);ε为l维高斯随机噪声或模型误差。如果将高光谱图像的n个像元(n为像元个数)均考虑进式(1)，则式(1)扩展为

式中，X∈Rl×n，其列向量为每个像元的光谱;S∈Rp×n，构成丰度矩阵或混合矩阵。图1为式(2)表示的线性混合模型示意图。对于线性混合模型而言，丰度矩阵S存在两个限制条件:非负性限制(sij≥0，i=1，2，…，p，j=1，2，…，n) 以及其和为1的限制

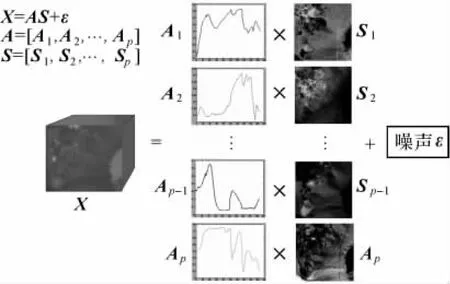
图1 线性混合模型示意图

三、非负矩阵分解

非负矩阵分解作为一种盲源分解(blind source separation，BSS)算法已经广泛应用于人脸识别和语义分析中，其具体过程为:给定非负矩阵X∈Rm×n和正整数p(p＜min(m，n))，非负矩阵分解的任务是寻找元素均为非负的矩阵A∈Rm×p和S∈Rp×n，满足

或等价地写为

式中，Xj为X的第j列列向量;Sj∈Rp;参数p为矩阵A的期望秩，并且一般情况下p为先验信息或者可以由数据X确定。一般认为A的列向量代表了数据X中潜在的信息，如具有物理意义的非负成分。这一特性使得非负矩阵分解广泛使用于数据分析、降维、特征提取、目标识别中。

解决NMF问题的很自然的方法就是通过最小化Y和AS之间的欧氏距离来寻找最优化途径。

式中，符号‖‖2F代表Frobenius模。

对于代价函数式(6)，许多文献提出了学习准则，其中解决这个最优化问题的常用方法是文献［3］中提出的乘法准则。该算法从两个正矩阵开始，每次迭代过程中，将A和S的元素乘以一些正因子，以证明该方法 Y－AS2F在乘法准则下单调非增。为了加速NMF的迭代算法过程，文献［4］提出了一种投影梯度限制的优化算法。非负矩阵分解经常遇到的问题就是局部最优，很明显的是，如果矩阵D为可逆矩阵，则AS=(AD)(D－1S)，因此NMF主要依赖于初始化和特定的学习策略。在很多应用中，需要通过增加限制条件来减轻NMF结果的非唯一性，将式(2)与式(3)比较不难发现，NMF具有使用于混合像元分解的潜力。

四、非负矩阵分解在光谱解混中的应用

混合像元分解的步骤主要包括数据降维、端元提取和丰度估计三部分，其中端元提取是混合像元分解的关键。端元提取算法的分类方法较多:根据是否假定光谱数据中存在纯像元，端元提取算法可分为两类:端元识别算法(endmember identification algorithm，EIA)和端元生成算法(endmember generation algorithm，EGA)，EIA直接从光谱数据中提取端元(即假定影像中存在纯像元)，算法的理论一般比较简单，而EGA是从光谱数据中产生端元，算法的过程较为复杂。对于多(或高)光谱数据而言，由于地面分辨率等因素的限制，在大多数情况下，数据中并不存在纯像元，因此，相对而言EGA提取的端元精度较高。NMF与线性混合模型具有一定的相似性:NMF通过线性结合寻找近似原始数据的非负基向量集，这些基向量的作用类似于端元。基于NMF的光谱解混算法不需要假定纯像元的存在，并且在提取端元的同时可以获取相应的丰度矩阵，属于EGA算法。NMF适合应用于高光谱数据解混，主要原因包括［5］:

1)高光谱数据的空间维数和光谱维数都很高;

2)高光谱数据本身、端元光谱及其丰度均为非负;

3)高光谱图像中，波段数大于图像中端元的个数。

文中重点对近年来学者们提出的 SC-NMF、MVC-NMF、APS-NMF算法步骤进行总结和分析。

1.SC-NMF算法

SC-NMF算法将平滑限制引入NMF中用于光谱解混、空间目标识别与分类。SC-NMF构建的目标函数为

SC-NMF算法的更新准则为

1) 初始化矩阵 Ai，j＞ 0 ，hi，j＞ 0 ，∀i，j;

2) 当 t=1，2，…(取最大迭代次数)时则

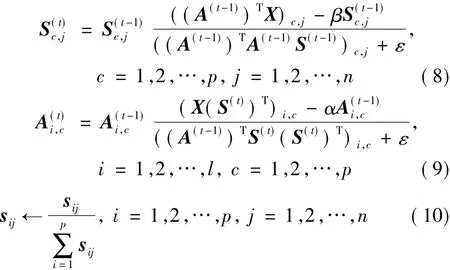
由此可见，SC-NMF采用的是乘法更新准则，与非负矩阵分解的梯度下降算法、交互最小二乘算法相比，其效率不高。文献［8］将SC-NMF算法应用于空间目标识别并与LEE的NMF算法［3］结果进行了比较，试验结果表明SC-NMF算法光谱解混的结果更优。

2.MVC-NMF算法

MVC-NMF通过将体积限制加入到NMF中将最小二乘分析和凸面几何结合起来。其提出的代价函数包括两部分，一部分为估量观测数据与端元和丰度重建数据之间的近似误差，另一部分由最小体积限制组成。文献［9］把这两部分作为两种力:外力(最小化近似误差)使估计结果向点云外部移动，内力(最小化单体体积)在相反方向上使端元尽可能地相互靠近。算法具体过程为:

1)构建目标函数

式中，1p为元素全是1的p维列向量;1n为元素全是1的n维列向量;J(A)为惩罚项，计算用估计的端元构成的单体体积;λ∈R。

2)初始化:从点云数据中随机选择p个点并将它们构成A的初始值，S矩阵也可以随机初始化，文献［9］在试验中将矩阵S初始化为零矩阵。

3)利用虚拟维(VD)估计端元数目p。

4)停止准则:给定迭代次数和误差阈值。

5)根据一定准则计算能够最小化目标函数的矩阵A、S，如果满足停止准则，则迭代停止，否则，更新矩阵A、S，继续寻找最小化目标函数的矩阵。

3.APS-NMF算法

APS-NMF算法认为邻域像素具有相似的丰度信息作为惩罚项引入NMF用于高光谱图像解混。APS-NMF的目标函数为

式中，Si表示丰度矩阵 S的列向量;表示第i个像素的邻域像素集。APSNMF利用交互投影梯度算法求解函数f(A，S)的最优解。文献［10］将APS-NMF算法应用于 AVIRIS高光谱数据，取得了一定的试验成果。

因为高光谱图像空间分辨率较低，邻域像素或许会差别比较大，将每个像素均同样考虑邻域像素的丰度相似性似乎不妥。

五、非负矩阵分解及其应用于光谱解混面临的困难

本文分析了线性混合模型与非负矩阵分解的定义及特点，总结了NMF适合应用于高光谱图像解混的原因，重点对近年来的 SC-NMF、MVC-NMF、APS-NMF算法步骤进行了介绍与分析。虽然人们针对非负矩阵分解开展了不少的研究，并且在实际中取得了很好的应用，但非负矩阵分解及其应用于光谱解混仍然面临一些问题。

1)初始化方法:好的初始化方法能够提高算法运行的速度、加快算法收敛，目前大多数算法还只是采用随机初始化方法进行初始化;

2)子空间选择:到目前为止，还没有确定最优p值(非负矩阵分解的最低阶数)的方法，该问题比较困难且常取决于实际应用;

3)最优化问题:目前，所有的NMF方法都存在该缺点，即求取的结果并非全局最优，而是局部最优解;

4)并行算法研究:由于大多数NMF方法存在双线性特性，因此可以研究非负矩阵分解的并行算法，提高算法的效率。

［1］PAATERO P，TAPPER U.Positive Matrix Factorization:A Non-negative Factor Model with Optimal Utilization ofError Estimates of Data Values［J］.Environmetrics，1994(5):111-126.

［2］LEE D D，SEUNG H S.Unsupervised Learning by Convex and Conic Coding［J］.Advances in Neural Information Processing Systems，1997(9):515-521.

［3］LEE D D，SEUNG H S.Learning the Parts of Objects by Nonnegative Matrix Factorization［J］.Nature，1999，401(10)，788-791.

［4］GILLIS N，GLINEUR F.Using Underapproximations for Sparse Nonnegative Matrix Factorization［J］.Pattern Recognition，2010，43(4):1676-1687.

［5］贾森.非监督的高光谱图像解混技术研究［D］.杭州:浙江大学，2007.

［6］MASALMAH Y M.Unsupervised Unmixing of Hyperspectral Imagery Using the Constrained Positive Matrix Factorization［D］.Puero Rico:The University of Puerto Rico Mayaguez Campus，2007.

［7］PARRA L C，SAJDA P，DU S.Recovery of Constituent Spectra Using Non-negative Matrix Factorization［J］.SPIE Proceedings，2003，5207(11):321-331.

［8］PAURA V P，PIPER J，PLEMMONS R J.Nonnegative Matrix Factorization for Spectral Data Analysis［J］.Linear Algebra and Applications，2006，416(7):29-47.

［9］MIAO L，QI H.Endmember Extraction from Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45(3):765-777.

［10］ZYMNIS A，KIM S J，SKAF J，et al.Hyperspectral Image Unmixing via Alternating Projected Subgradients［C］∥Proceeding of 41st Asilomar Conference on Signals，Systems，and Computers.Pacific Grove，CA:［s.n.］，2007.

Discussion of the NMF’s Application for Hyperspectral Imagery Unmixing

LI Ersen，ZHANG Baoming，YANG Na，YANG Jingyu，GUO Xiaogang

0494-0911(2011)03-0007-04

P237

B

2010-01-08;

2010-06-23

矿山空间信息技术国家测绘局重点实验室(河南理工大学，河南省测绘局)开放基金资助项目(KLM200904)

李二森(1984—)，男，河南新安人，博士生，主要研究方向为高光谱图像处理和模式识别。