一类矩阵方程最小二乘问题的LSQR方法

胡善瑞，王明辉，田保光

(青岛科技大学数理学院，山东青岛266061)

一类矩阵方程最小二乘问题的LSQR方法

胡善瑞，王明辉，田保光

(青岛科技大学数理学院，山东青岛266061)

讨论了对称斜反对称矩阵的结构，应用LSQR方法求解最小二乘问题‖XTAX－B‖=min(A为待求对称斜反对称矩阵)，并给出了相应的算法及数值例子．

对称斜反对称矩阵;LSQR方法;最小二乘问题;矩阵拉直①

0 引言

约束矩阵方程问题在结构动力学、分子光谱学、电力学、参数识别、生物学、热力学、线性最优控制、自动控制理论等领域有着重要的应用．目前为止，约束矩阵方程在涉及对称矩阵等问题，应用SVD、GSVD、QSVD、Schur分解等已取得丰硕的成果［1－4］.近年来，随着求解约束矩阵方程问题的研究不断深入，一些新的问题不断被提出和解决，人们在讨论解的存在性的同时也提出了许多有效的数值方法［5－7］.

考虑约束最小二乘问题

其中X∈Rn×m，B∈Rm×m为给定矩阵，A∈ASn为待求矩阵.

对于该问题，周硕和吴柏生［8］已经提出了一种求最小二乘解的方法，即应用矩阵标准相关分解(CCD)的方法，推导给出了A的表达式;但由于矩阵分解的方法针对较大型矩阵时，计算量过于庞大，此时不宜采用直接方法.这里，我们提出一种迭代算法，即将LSQR［9］方法应用到问题(1)，得到一类算法，进而求解问题的最小二乘解.

在本文中，我们记所有n×m阶的矩阵的集合为Rn×m;所有n阶对称斜反对称矩阵的集合记为ASn;‖A‖代表矩阵A的Frobenius范数;A⊗B表示两个矩阵A与B之间的Kronecker乘积;vec(A)表示对矩阵A中的元素按列作拉直运算组成的一组向量.

1 等价问题

最小二乘问题(1)的约束条件为A∈ASn，需要将约束条件进行无约束转化，在这之前，我们先考察ASn的结构问题.

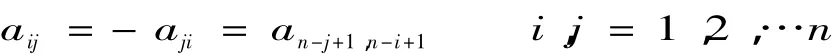
定义1［10］当矩阵A∈Rn×n中的元素关于对角线是反对称，并且关于反对角线是对称，即满足时，我们称A为对称斜反对称矩阵.满足条件的矩阵A的集合记为ASn.关于对称斜反对称矩阵的逆特征值及其近似解的问题都已有所讨论［10］.

记

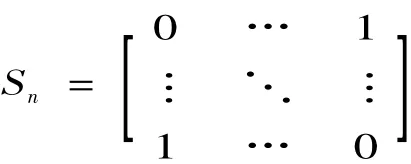
且k=［n/2］(即k为不大于n/2的最大整数).

当k=2n时，令

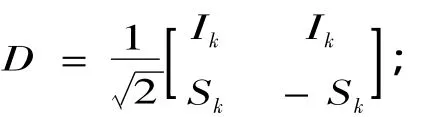
当k=2n+1时，令

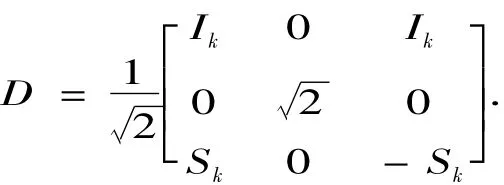
引理1 DTD=I.

引理2［10］A∈ASn当且仅当

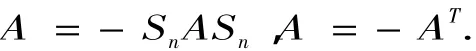
引理3［10］A∈ASn当且仅当

记DTX=，其中X1∈R(n－k)×m，X2∈Rk×m.由上面的讨论及引理，我们得到下面的定理:

定理1 最小二乘问题

等价于

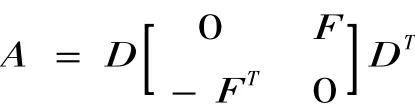
这里F为

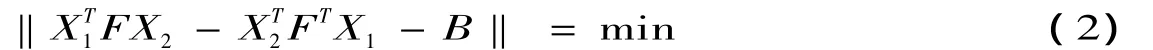
的最小二乘解.

证明:因为A∈ASn，由引理3，存在D∈Rn×n，F∈R(n－k)×k使

另一方面，

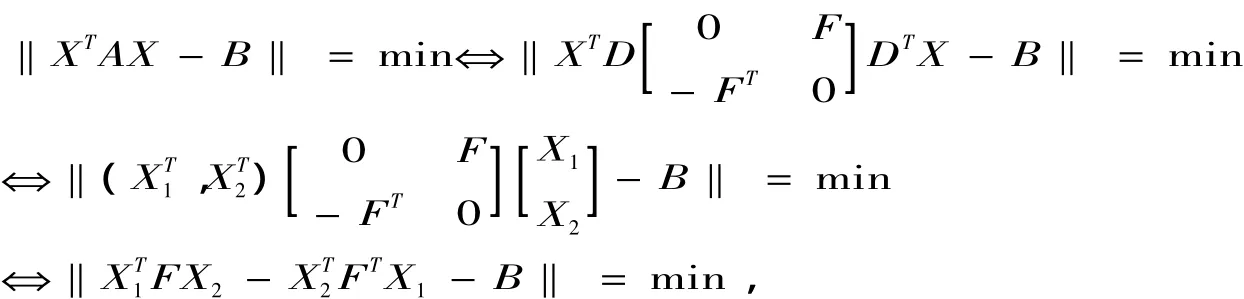
定理得证.

2 最小二乘问题(2)的LSQR方法

2.1 LSQR方法简单回顾

Paige与Sauders于1982年提出的LSQR算法［9］，用以解决下面的最小二乘问题:给定A∈Rm×n，b∈Rm，计算x满足

它的法方程为

考虑到文献中已经有详细的讨论，这里我们简单给出它的算法:

1 初始化

2 迭代，对于i=1，2，…

(1)双对角化

(2)构造和应用Householder变换

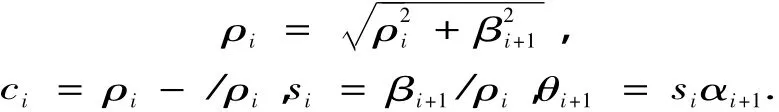
(3)更新xi和hi+1

3 检查收敛性.

易知，如果(4)有解x*∈R(ATA)=R(AT)，那么x*是(3)的极小范数解，显然，由LSQR算法得到的xk属于R(AT).

2.2 最小二乘问题(2)的LSQR算法

考虑最小二乘问题(2)，我们需要先将其转化为向量的形式，再应用LSQR算法.

引理4［11］对于任意的S1∈Rm×n，S2∈Rp×q，定义p(l，k)形式如下:

则

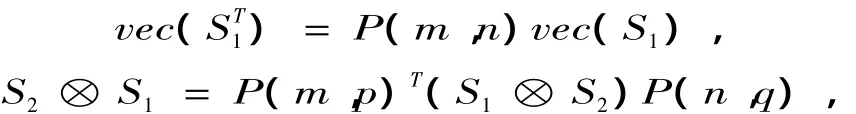
这里P(i，j)=P(j，i)T=P(j，i)－1.由此，我们得到如下定理:

定理2最小二乘问题

等价于

证明:对

对矩阵作拉直运算

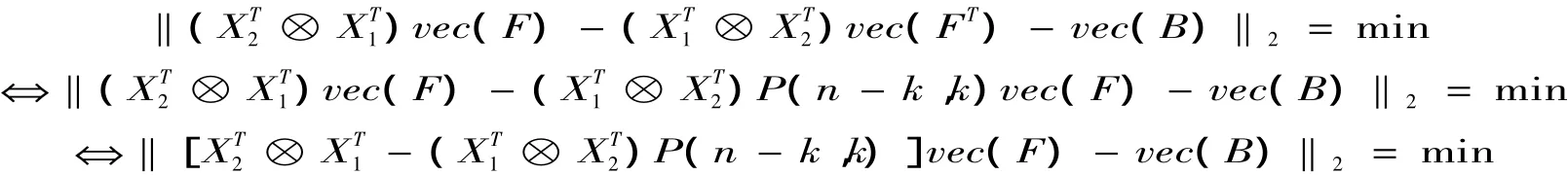
记

则问题化为

定理得证.

下面对‖Mx－b‖2=min应用LSQR方法，把其中的向量迭代写成矩阵的形式，从而避免Kronecker积的出现.为此，我们需要把LSQR方法中的v和u转化成矩阵V和U，因此必须先把MTu和Mv转化成矩阵形式.

用符号mat(a)表示向量a的矩阵化，在这里也是算子vec的逆运算，对v∈Rk·(n－k)，u∈Rm2，令V=mat(v)∈Rk×(n－k)，U=mat(u)∈Rm×m，则我们有

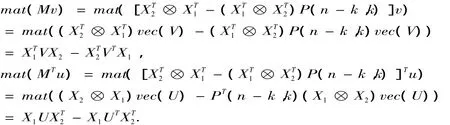
现在，我们给出求解问题(2)的LSQR算法:

1 初始化

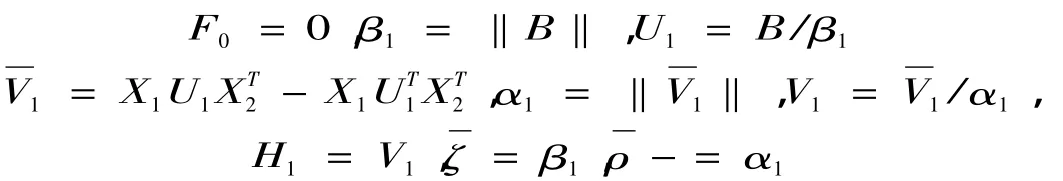
2 迭代，对于i=1，2，…

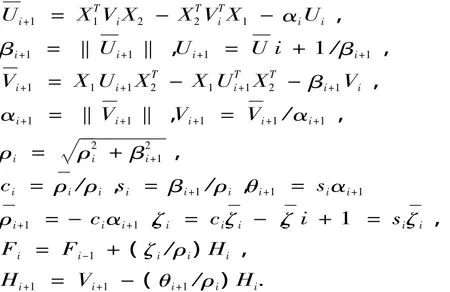
3 检查收敛性.

注2:当XTAX=B是相容方程时，由算法可以计算它的极小范数解.

3 数值例子

本节通过两个例子看看算法的执行情况，所有结果都是在matlab7.0运行得到.

例1考虑矩阵方程XTAX=B，其中

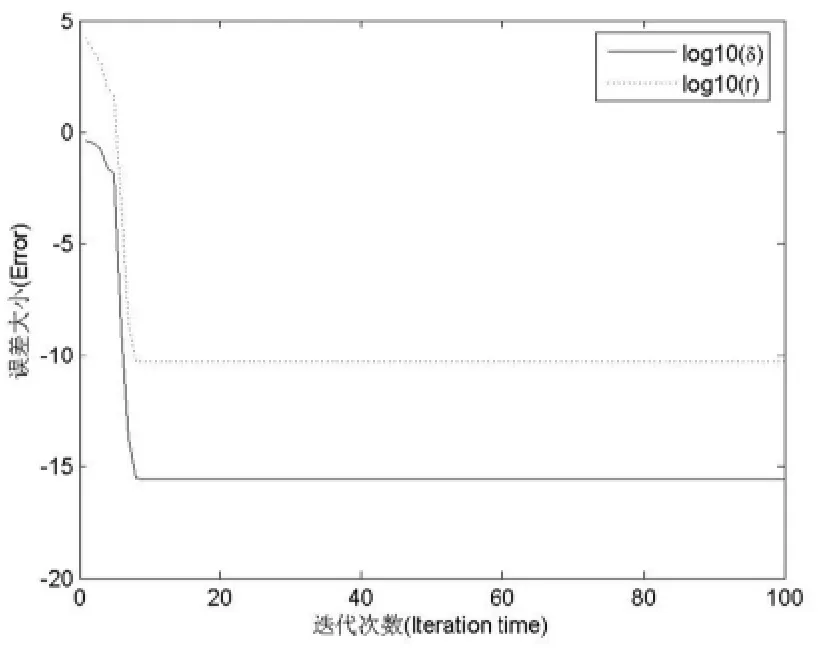
图1(Fig.1)

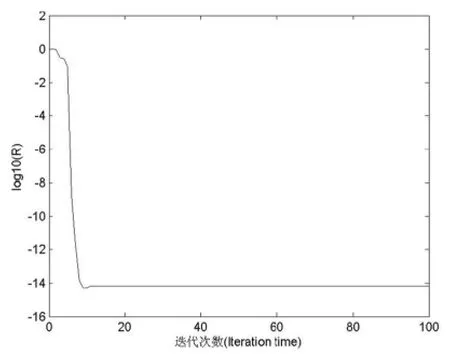
图2(Fig.2)

可以验证方程是相容的，而且有唯一解

应用上面的算法，当迭代进行到第k步，得到Fk，进而可求得Ak.我们以δk=‖Ak－A*‖/‖A*‖表示解的相对误差，rk=‖B－XTAkX‖表示残差，计算结果见图1.可见，随着迭代的进行，δk和rk最终趋于一个稳定值(如图1)，其对应解为最优解.

例2对于‖XTAX－B‖=min(A∈ASn为待求)，已知

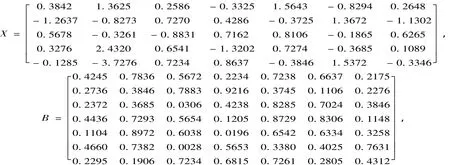
求解问题的最小二乘解.

用上面的算法进行计算时，考虑(2)的法方程.由(5)可得法方程为MTMx=MTb，通过一系列变换(矩阵与向量之间的转换)得到

记

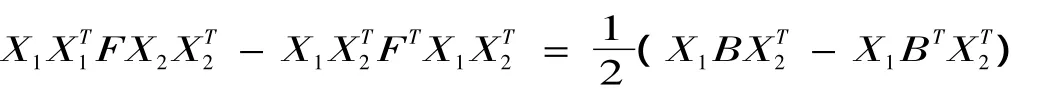
为迭代进行到第i步的残量.则由图2可以看到，随着迭代的进行，当迭代到第11步以后的时候，残量值趋于稳定，此时迭代得到的解A为最优解，并且有

［1］臧正松．矩阵方程AXB=C的实部半正定解［J］．华东船舶工业学院学报，2002，16(02):50－53．

［2］彭振赟．几类矩阵扩充问题和几类矩阵方程问题［D］．湖南大学数学与计量经济学院，2003．

［3］廖安平，白中治．矩阵方程A^TXA=D的双对称最小二乘解［J］．计算数学，2002，24(1):9－20．

［4］袁仕芳，廖安平，雷渊．四元数体上矩阵的最小化问题［J］．数学物理学报，2009，29A(5):1298－1306．

［5］Sun Jie．The Iterative Method for the Solution to the Restricted Matrix Equation［J］．Journal of Shanghai Institute of Technology，2007，7(01):4－9．

［6］田兆禄．线性方程组Ax=b和矩阵方程Sylvester的迭代解法［D］．上海大学，2008．

［7］Fang Ling，Li Bo and Fu Shilu，et al．Iternative Solutions of the Inconsistent Matrix Equation AXB=D in Anti－centrosymmetric Matrix Set［J］．Journal of Logistical Engineering University，2010，26(04):86－91．

［8］Zhou Shuo and Wu Bai－sheng．Least－square Solutions of Inverse Problems for Anti－symmetric and Skew－symmetric Matrices．Northeast．Math．J，2007，23(3):189－199．

［9］C．C．Paige and A．Saunders．Lsqr:An Algorithm for Sparse Linear Equations and Sparse Least Squares．ACMTrans．Math．Software，1982:8(1):43－71．

［10］Xie Dongxiu and Sheng Yanping．Inverse Eigenproblem of Anti—Symmetric and Persymmetric Matrices and Its Approximation，Inverse Problems，2003，19:217－225．

［11］R．A．Horn and C．R．Johnson．Topics in Matrix Analysis［D］．Cambridge University Press，Cambridge，UK，1991．

［责任编辑:陈庆朋］

Abstract:The structure of anti－symmetric and skew－symmetric matrix is discussed．The LSQR method is applied to solve the least－square problem‖XTAX－B‖=min(where A is a anti－symmetric and skew－symmetric matrix)and the corresponding arithmetic together with some numerical examples are given．

Key words:anti－symmetric and skew－symmetric matrix;the LSQR method;least－square problem;matrix straighten

The LSQR Method to the Least－square Problem of a Class of Matrix Equation

HU shan－rui WANG Ming－hui TIAN Bao－guang
(College of Mathematical and Physical Sciences，Qingdao University of Science＆Technology，Qingdao 266061，China)

O151

A

1004－7077(2011)02－0051－06

2011－01－27

国家自然科学基金资助项目(11001144)

胡善瑞(1987－)，男，山东济宁人，青岛科技大学数理学院应用数学专业2009级在读硕士研究生，主要从事数值代数方向的研究．