一维非齐次边值问题的有限元法
2011-01-02赵月坤高常
赵月坤,高常
(枣庄职业学院 271000)
0 引言
有限元方法是在Ritz-Galerkin方法的基础上改进得到的.它改进了传统Ritz-Galerkin方法,将求解区域剖分成有限个单元,在每个单元上构造插值函数,再由此得到在整个区域上的插值函数.由于插值基函数是局部的,这不仅大大的减少了计算量,而且极易处理本质边值条件.(参见文献[1-5])本文给出了有限元方法求解一类非齐次两点边值问题的有限元格式,讨论了齐次与非齐次问题有限元方法之间的关系.用数值算例比较了有限元法与传统Ritz-Galerkin方法计算结果.
1 非齐次两点边值问题的Ritz-Galerkin解法
非齐次两点边值问题的有限元方法,基本思路是首先将问题转化为齐次的情况,利用齐次两点边值问题的有限元方程推导非齐次问题有限元方程.
1.1 非齐次边值问题齐次化
考虑一类非齐次两点边值问题
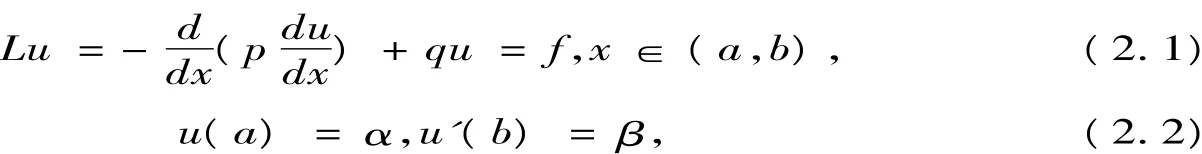
其中p∈C1(I)(一次连续可微函数空间)
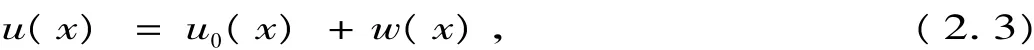
其中u0(x)满足例如取u0(x)= β(x-a)+α.将(2.3)代入(2.1),
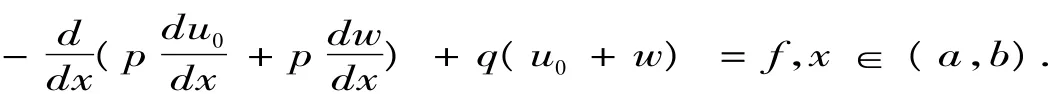
整理得
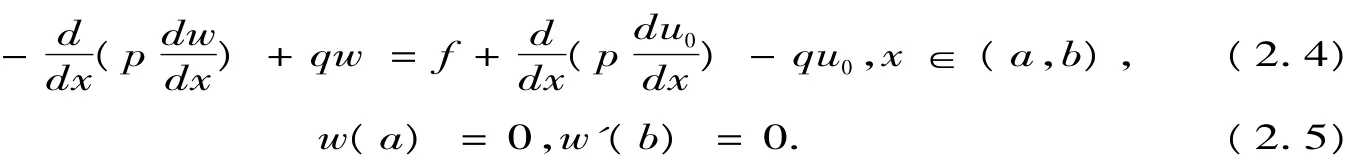
至此,我们将非齐次边值问题转化为齐次边值问题.
1.2 齐次两点边值问题的变分形式及Ritz-Ga lerkin方法
为了求解非其次边值问题,先来了解齐次两点边值问题的Ritz-Ga lerkin方法(参阅[2]) .
考虑齐次两点边值问题
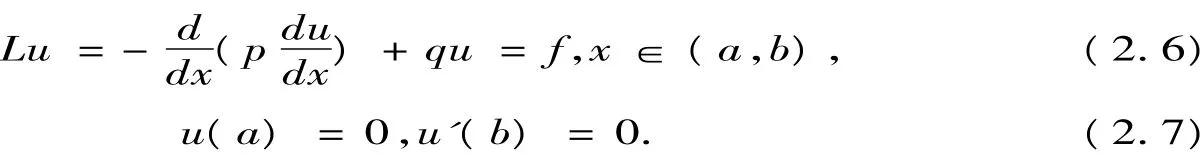
根据虚功原理,若u∈C2(I),则u是边值问题(2.6),(2.7)的解的充要条件是:u且满足变分问题 a(u,v) - (f,v)=0,对任意
设Vn是的n维子空间,φ1(x),φ2(x),…,φn(x) 是 Vn的一组基函数,则Vn中任一元素可表示为方法离散格式为:求系数c1,c2,…,cn,使得un关于 v∈Vn满足a(u,v) - (f,v)=0.对任意即
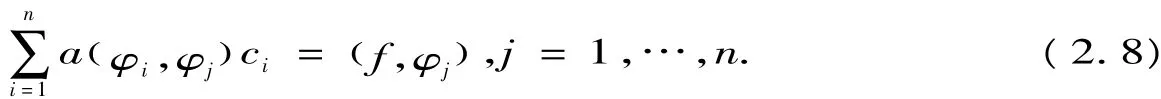
称(2.9)为Ritz-Galerk in方程组.方程组(2.9)的系数矩阵
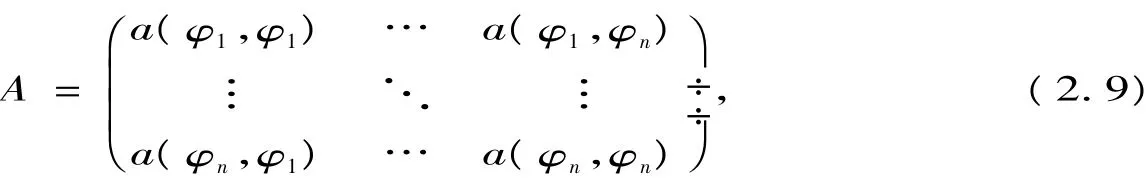
是对称正定的,故(2.9)是唯一可解的.
1.3 非齐次两点边值问题的Ritz-Galerk in方程
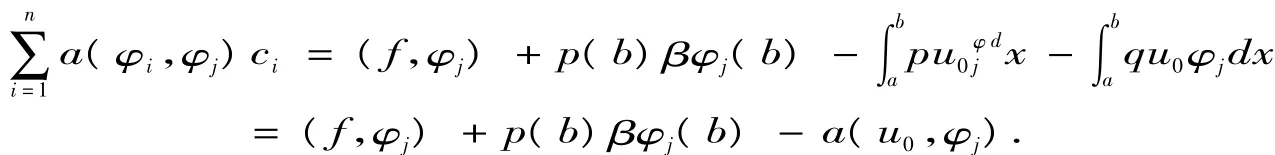
即非齐次两点边值问题(2.1)、(2.2)的Ritz-Galerk in方程组为
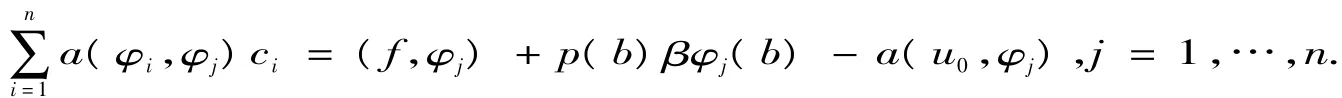
2 有限元法
有限元法在很大程度上克服了Ritz-Ga lerkin法选取基函数的固有困难,应用样条函数方法提供了一种选取“局部基函数”或“分片多项式空间”的新技巧.
2.1 齐次两点边值问题的有限元方程
对区间 I= [a,b]进行剖分.设x0,x1,…,xn满足a=x0< x1< … < xn=b,称xi为节点,ei= [xi-1,xi]为单元,hi=xi- xi-1为单元 ei的长度,记
取 m=1,设函数在节点上取值为 u0=0,u1,…,un.在单元 Ii,Ii+1考察线性插值:对节点xi构造山形函数φ1(x),φ2(x),…,φn(x),它们组成Uh的基.分段线性插值函数uh可表示为
Ritz-Ga lerkin方程组的系数矩阵(2.9)中的非零元素为
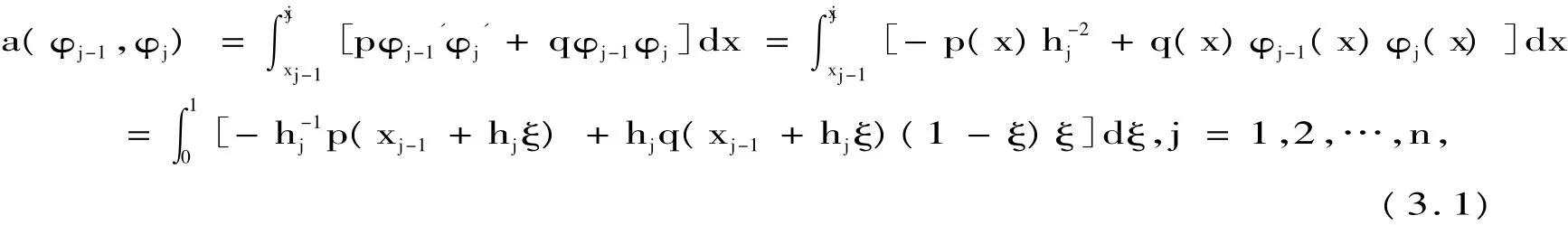
以及
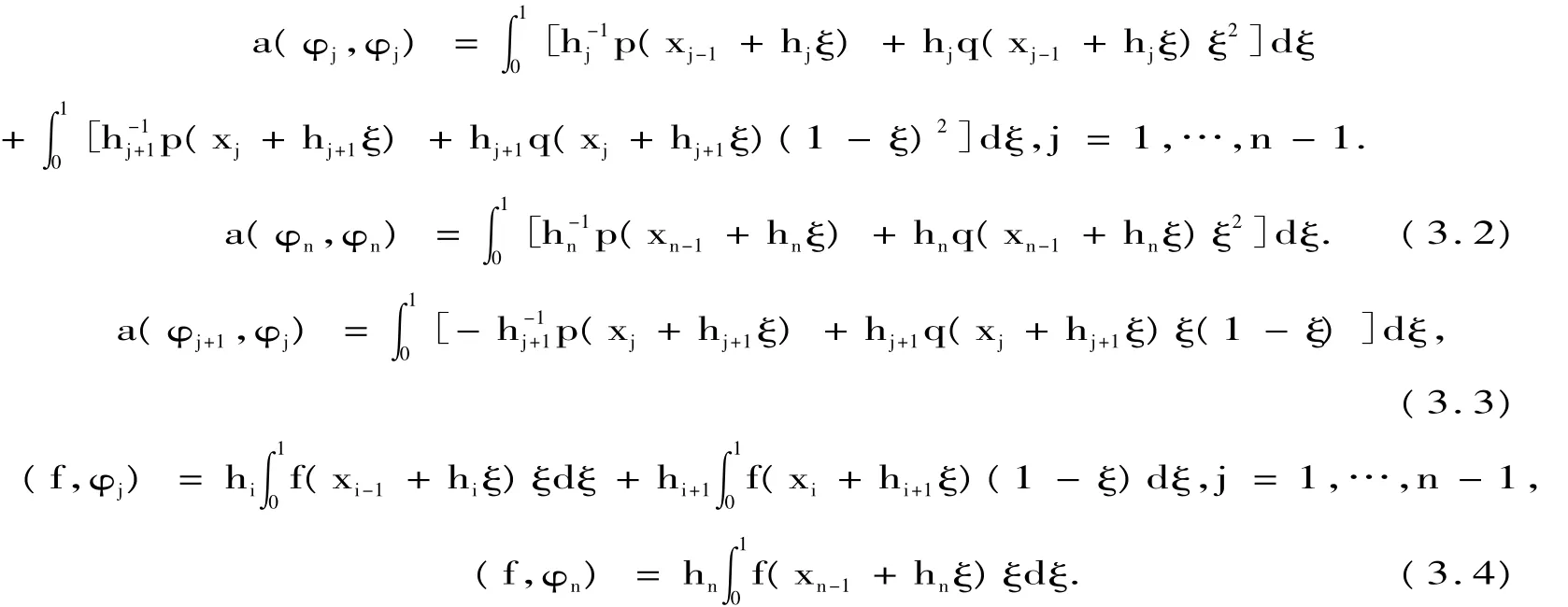
2.2 非齐次边值问题的有限元法
考虑非齐次边值条件,增加基函数
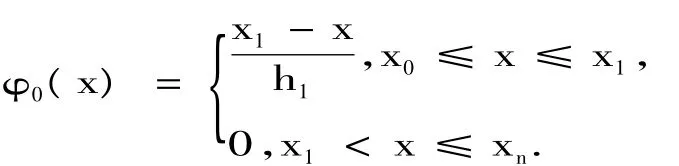
令u= αφ0+w,仿照2.3中的做法,用代替(3.4) 中的 f,有

即非齐次两点边值问题(2.1),(2.2)的有限元方程组为
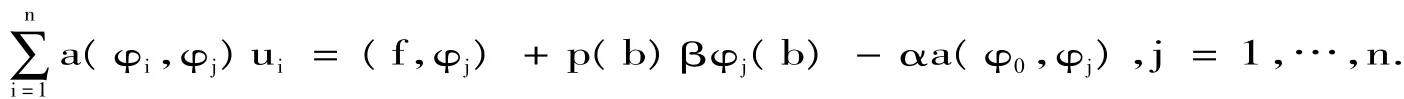
4 算例
例1 用传统Ritz-Ga lerkin方法解非齐次两点边值问题
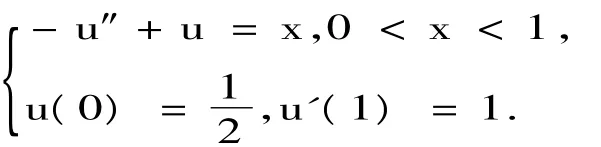
例2 用有限元方法解例1,即
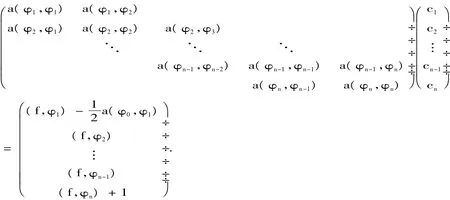
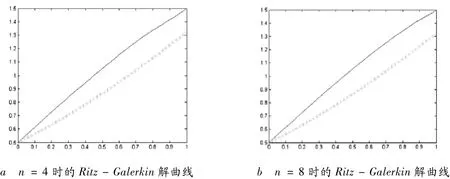
图 4.1
用M a tlab编程计算得到精确解与数值解的对照,如图4.2.从图4.1和图4.2看出有限元解曲线比Ritz-Galerk in解曲线吻合性更好,而有限元法的计算更简便.

图 4.2
[1]赵静,但琦.数学建模与数学实验[M].北京:高等教育出版社,2003.
[2]李荣华.偏微分方程数值解法[M].北京:高等教育出版社,2005.
