环量控制尾梁参数对直升机尾梁侧向推力的影响

董振兴，高亚东，王华明

(南京航空航天大学直升机旋翼动力学重点实验室，江苏南京 210016)

0 引言

无尾桨概念(NOTAR)是直升机技术的新发展，它改变了传统的尾桨设计概念，利用环量控制尾梁提供旋翼反扭矩所需的力，从而取消尾桨，从根本上解决尾桨给直升机带来的各种问题。其结构简单，安全性好，改善了可靠性和维护性，减少了直升机的振动和噪声，使乘坐舒适性得到改善。

环量控制由边界层控制发展而来，指的是后缘为圆弧形的翼型后部上表面开缝，从缝中喷出气流，挟带着上面的气流绕后缘流动，直到后缘附近某点分离，这样在该翼型上形成环量，产生升力。普通翼型的上表面气流不可能绕过尖削后缘，而是在后缘分离。环量控制翼型后缘为圆弧形，圆柱［1-2］就是这种翼型的特例。无尾桨直升机，就采用了环量控制技术。这种直升机的机身为圆柱或近似为圆柱，以旋翼的尾流为来流，在机身上引出壁面喷流后，产生一侧向力以平衡旋翼的扭矩，从而取代了尾桨，简化了直升机的设计。

1 计算模型

1.1 建立几何模型

MD520N是一架技术成熟的无尾桨直升机，它采用的环量控制尾梁缝隙宽度与尾梁直径之比h∶D=0.009，缝隙长度与旋翼直径之比为 0.18。参照该机型数据以及文献［3］，建立本文的计算模型。模型的主要参数如表1所示。

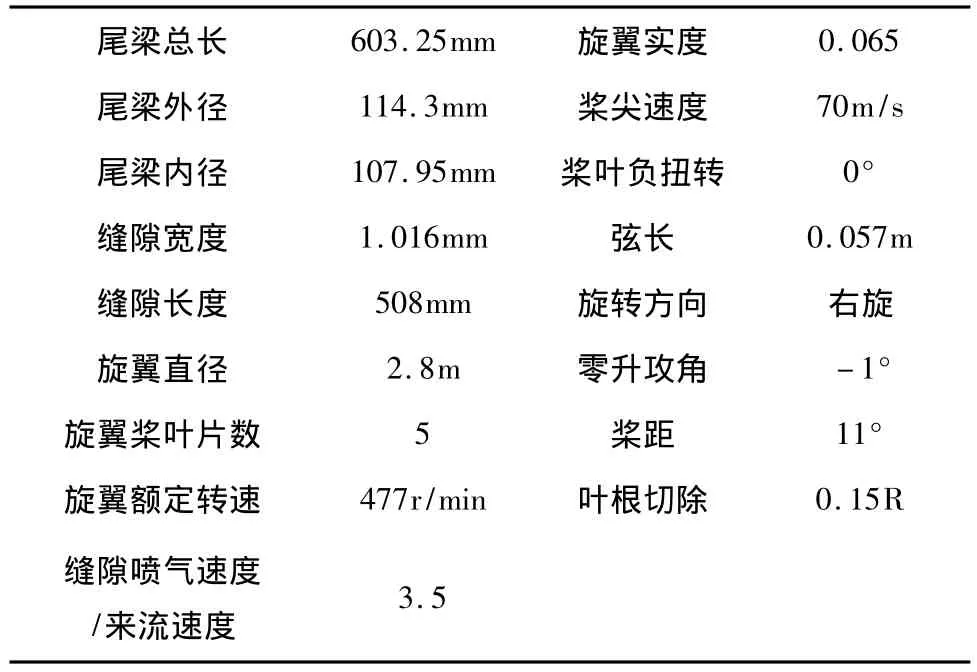
表1 旋翼及尾梁模型主要参数

动量源方法［4］是把桨叶对气流的作用以动量源的形式来表示，并忽略桨叶附近流场的细节特征，把周期性流动通过时间平均转化为“准定常”流动。在保证旋翼下洗流流场本质属性的前提下，上述方法舍去求解旋翼桨叶周围流场的流动细节给计算精度提出的高要求。同时，由于用围绕整个桨盘的网格来取代围绕桨叶的贴体网格，减小了网格生成难度和网格数目，有效节省了计算时间。确定动量源项需要通过配平获得，根据力平衡关系得到输入参数并加入到自定义函数中，实现动量源项的模拟。一般计算流程如下:已知旋翼的转速、来流速度和桨叶几何参数，使用叶素理论求出桨叶微段在剖面坐标系下的升力、阻力，然后通过坐标变换，把桨叶微段在剖面坐标系下的受力情况转化为在计算域坐标系下的受力情况，得到桨盘前后的压力差，即为动量源。本文采用动量源方法模拟旋翼下洗流流场，旋翼桨叶将由桨盘模型(圆盘)代表，即通过桨盘对流场力的作用来模拟旋翼桨叶对流场影响。由于本文主要研究环量控制尾梁的工作原理，以及风洞和旋翼下洗流中动量系数、缝隙几何参数等对尾梁气动力的影响，所以工作重点是建立环量控制尾梁分析模型，对机身则进行了适当的简化处理。除此之外，为减少后期网格划分工作量，降低网格生成难度，本文对几何模型作了合理简化:

1)对尾梁的简化处理。把真实的尾梁简化为一个圆柱体，并在适当位置开缝。由于喷气锥侧向喷气，产生侧向力，且处于尾梁尾部对环量控制影响不大，所以未在模型上构建。

2)对旋翼的简化处理。把真实的五片桨叶简化为一个等半径的作用盘，除去中间桨毂部分，在计算时向桨盘的面网格单元载入动量源项。

利用三维设计软件CATIA建立机体模型，主要采用曲面造型设计和分块设计两大模块来完成，最后封闭成一个实体，再检查连续性，避免出现开口，生成模型如图1所示。

图1 机体三维模型

1.2 建立计算域

为了更好地模拟尾梁气动特性，本文建立了一个长为10m，半径为2m的圆柱形计算域。为了减少网格数量，提高计算效率，把圆柱形计算域与机身之间的区域分为4个部分，从外到里分两层，外层为一个区域，内层从前到后依次为入口段、中间段与出口段。

1.3 划分网格

为了简单而准确地满足边界条件，首先生成贴体(单域)计算网格，即附面层网格，然后分区域划分体网格，即根据外形特点将总体流场分成若干子域，对每个子域分别建立网格。本文中机身和尾梁表面(不含缝隙)采用非结构三角形网格，缝隙处采用四边形结构网格，两侧小三角面采用非结构网格，旋翼用一圆盘来代替，在圆盘上划分结构化网格，除去中间桨毂部分，体网格从内向外逐块生成，首先生成缝隙喷口处小体的结构六面体网格，然后生成内层小体的非结构四面体体网格，最后是中间层和外层的结构六面体网格，从而完成整个计算域网格。体网格生成需要花费较多时间，需进行初始化与细化等操作，完成后约为216万体网格。

2 计算结果及分析

本文采用k-ε湍流模型，由于旋翼下洗流速度不高，考虑气流粘性影响，计算时控制方程采用了定常、不可压、有粘的纳维尔-斯托克斯方程［5］，将动量源程序导入到FLUENT软件中模拟旋翼下洗流，根据下洗流的速度改变缝隙的喷气速度，即改变动量系数，得到了尾梁模型上气动力随缝隙数目、大小和位置、动量系数等基本参数的变化情况。

2.1 表面压力分布

图2给出无环量控制(缝隙不喷气，Cμ=0)时尾梁压力分布曲线。曲线1表示通过势流理论计算的结果。曲线2和3分别为模拟旋翼下洗流和风洞流场中尾梁表面压力分布。由于尾梁表面分离区压力基本保持不变，曲线平坦，曲线端点就是分离点。从风洞中尾梁表面压力分布曲线可知分离点大约在75°附近，而在旋翼下洗流中的压力分布曲线上，分离点分别在150°和240°附近。从圆柱体边界层分离理论可知，分离点位置不但与雷诺数有关，还与模型表面粗糙度和来流紊流度有关。实际旋翼下洗流不是垂直下降的，而是螺旋下降的极不稳定的气流，其紊流度很高，尽管雷诺数较低，但紊流使尾梁表面边界层在分离前就已经由层流过渡到紊流，使分离点后移，引起负压增大，因而图2中曲线2的最高点(驻点)并不在0°，而是在10°左右，这是由于旋翼下洗流并不是垂直下降的，而是呈螺旋形斜向下打到尾梁上，相对尾梁顶部存在大约10°的夹角，使分离点推迟10°，即分离点距前驻点140°。

图2 尾梁表面压力分布

图3 有环量控制时尾梁截面附件流场流线图

图3为尾梁附近流场流线，从图中看出当有环量控制时，缝隙喷出气流给尾梁表面气流增加能量，使气流大量流向尾梁未开口的一侧，局部负压大大提高，分离点后移，造成尾梁两侧压力分布不对称;处于90°一侧的尾梁表面负压显著增加，而另一侧变化不大，从而在尾梁上产生指向负压较大一侧的侧向力。其中，尾梁尾部的环量控制效率低于中部。在尾梁与机身的结合处气流分离严重，对旋翼下洗流干扰严重，导致单缝随方位角变化时，尾梁气动力变化剧烈，环量控制效率较低。因而，环量控制效率沿尾梁从前到后的顺序先逐渐变高后逐渐变低，同时也决定了单缝不适合工程应用。

2.2 动量系数的影响

从图4中C1随Cμ的变化曲线可以看出，同前期风洞流场中相似，处于旋翼下洗流内的尾梁的升力(侧向力)系数C1随动量系数Cμ的增大而增大，开始曲线斜率较大，当Cμ＞0.4时逐渐变得平缓，综合考虑阻力系数和升阻比后得出最优动量系数Cμ大约在0.4附近，此时环量控制效率最高。该规律与麦道公司的风洞实验结果［6］相符。

2.3 缝隙几何参数的影响

对于旋翼下洗流中缝隙大小和位置对环量控制尾梁气动力的影响如图5中所示，缝隙宽度越大，升力系数越小，且与风洞中单缝最佳位置不同，在旋翼下洗流流场中，单缝开在140°方位时升力系数最大，环量控制效果最好，该结论与文献［7］研究结果相符。

图5 升力系数随方位角变化的曲线

前期的研究发现，风洞中最佳双缝位置之间的夹角是60°，旋翼下洗流中气流速度与尾梁纵向对称面的夹角的影响可看作是缝隙位置的影响，可按照这个夹角以及缝隙方位角由小到大的顺序，缝隙宽度前小后大的布置方式建立模型。改变缝隙的位置，计算双缝在不同位置时尾梁气动力的变化。图6表示升力系数、阻力系数和升阻比随双缝方位角变化规律，其中横坐标是第一条缝的方位角。当第一条缝位于140°，即双缝方位角分别为80°和140°时，升力系数Cl最大，此时升阻比Cf也最大。麦道公司无尾桨直升机MD520N的环量控制尾梁双缝正是这两个值［3］。由此确定在旋翼下洗流中双缝最佳方位角为80°和140°。

图6 升、阻力系数和升阻比随双缝方位角变化的曲线

3 结论

本文主要研究了处于旋翼下洗流中的环量控制尾梁的气动特性，以及动量系数、缝隙几何参数等对尾梁侧向气动力的影响。

1)通过仿真计算，并与以往实验对比，环量控制尾梁最佳动量系数在0.4附近。

2)对于单缝，最佳方位角为140°;对于双缝，双缝的最佳位置为80°和140°。

3)双缝环量控制效率比单缝高，适用于工程应用。按方位角从小到大的顺序，缝隙宽度采用前小后大方式布置时，环量控制效率明显大于前大后小的布置方式。

［1］Sun M，Pai S I.Aerodynamics force calculations of an elliptical circulation control airfoils［J］.J of Aircraft，1996，23(9):679-680.

［2］Ghee T A ，Leishman J G.Unsteady circulation control aerodynamics of a circular cylinder with periodic jet blowing［J］.AIAA J，1992，30(2):289-299.

［3］Fisher D T.Wind Tunnel Performance Comparative Test Results of a Circular Cylinder And 50%Ellipse Tailboom for Circulation Control Ant-torque Application［D］.Thesis of Naval Postgraduate School.March，1994.7-30

［4］王博.基于CFD方法的直升机旋翼/机身流场模拟及分析［D］.南京:南京航空航天大学，2007.20-30.

［5］钱翼稷，编著.空气动力学［M］.北京:北京航空航天大学出版社，2005.2.65-70.

［6］Logan，A H.Evaluation of a Circulation Control Tail Boom for Yaw Control［M］.Hughes Helicopters，Inc.，USARTL-TR-79-10，April 1978.10-20.

［7］Chaffin M S，Berry J D.Navier-Stokes simulation of a rotor using a distributed pressure disk method［C］.Proceedings of 51st Annual Forum of AHS，1995.25-45.