提高速动保护精确性滤波新算法

叶 飞，刘观起，胡道徐，张 进，纪 卉

(1.华北电力大学 电气与电子工程学院，河北，保定 0710032;2.思源弘瑞自动化有限公司，上海 201108)

0 引言

微机保护是通过对电力系统故障后电流、电压信号的基频分量的提取分析［1］。从故障暂态信号中快速、准确的提取电流、电压的基频分量成为继电保护算法的关键。目前常见的微机继电保护算法有全周波傅里叶算法、半周波傅里叶算法、差分傅里叶算法、最小二乘法和卡尔曼滤波算法。

数据窗越长、采集的数据越多，则测量的精确度越高，然而数据窗越长，等待数据采集所需的时间就越久，继电保护动作越滞后［2］。全波傅里叶算法虽然能够完全滤除稳定的直流分量和整数次谐波，并且能较好地滤除线路的分布电容引起的高频分量，对随机干扰信号的反应也较小，而对畸变波形中的基频分量可平稳和精确地做出响应，但是全周波傅里叶算法需要一个周期的完整数据，即需要采集20 ms内的所有数据，无法满足保护的速动性。半周波傅里叶算法，虽然只需要10 ms数据窗，不但无法有效的滤除衰减直流分量和偶次谐波，而且对偶次谐波有一定的放大作用，对低频分量抑制效果不好，容易造成保护误动。差分法滤波能够完全滤除稳定的直流分量，并在一定程度上抑制输入信号中的非周期分量［3］，但增强了对高次谐波的响应，对高次谐波有放大作用，使得对傅里叶算法的幅频特性变坏。最小二乘法从频域角度上属于全零点滤波器，在使用时其拟合模型的选择应与前置低通滤波器相配合，从而使得未包含于拟合模型中的高频分量能够得到很好的抑制，为了保证算法拥有较好的估计精度，拟合模型不得不扩大包含所有通过低通滤波器的谐波分量，这将导致数据窗加长、计算量加大。当故障信号和干扰信号的分布特性难以准确估计时，最小二乘法无法保证滤波精度和暂态时延［4］。卡尔曼滤波法事最优估计理论中的一种算法，主要用于随时间变化的状态量的估计［5］。在处理噪声衰减时，对于不同时刻的残差平方值施加不同的加权系数，但由于故障后的稳态分量受故障点位置、系统运行方式、故障初始相角等随机因素的影响，其噪声参数的在线估计过于复杂导致限制了应用范围。

本文描述一种通过零、极点配置法形成的狭窄带通滤波与半周波傅里叶算法相结合的新算法，狭窄带通半波算法能够快速、有效地提取基频分量，抑制了非周期分量、低频分量对半周波傅里叶算法的影响，整个算法对数据的需求量只需要故障后半个周波再加一个数据，满足了微机保护快速响应，同时也提高了半波傅里叶算法的滤波精度。

1 半周波傅里叶算法

1.1 半周波傅里叶算法原理

半波傅里叶算法的积分区间0～π/2，利用半个周波的采样值来计算电流电压基波分量的正弦和余弦系数，其矩阵法计算公式为

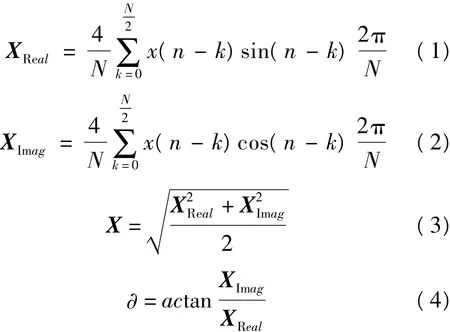
式中:XReal，XImag分别表示进过半波傅里叶计算后的实部、虚部;N为一周期内采样点数目;∂初始相角。

电力系统中电流、电压波形为正弦，其半波傅里叶算法的幅频特性如图1所示。

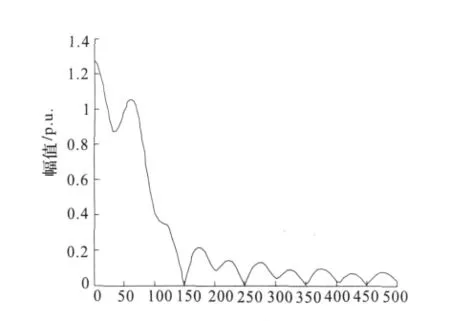
图1 半波傅里叶算法的幅频特性Fig.1 Spectral response of the half－cycle discrete Fourier transform

1.2 谐波、衰减直流分量影响

电力系统发生故障时，故障电流中不但包含基频分量，同时还会产生较大的衰减直流分量和高次谐波分量［7］。

衰减直流分量在频域上具有连续的频谱，其频率主要集中在低频段内，从图1可以看出，半波算法对指数衰减的非周期分量呈现了很宽的连续频谱，半周波傅里叶算法无法滤除衰减直流分量及其低频分量，所以衰减直流分量和低频分量对半周波傅里叶算法的影响很大［8］。从式 (1)、(2)可以看出，半波傅里叶算法能够完全滤除奇次谐波，但不能滤除偶次谐波，故障电流中的包含的偶次谐波将对傅里叶计算的结果产生影响。

由于半波傅里叶算法无法滤除偶次谐波分量和低频分量，提取基频周波的精度较低，但半波傅里叶算法只需要半个周波的采样数据，具有响应速度快的优势。

2 狭窄带通半周波算法

2.1 零极点配置法设计带通滤波器

一个N阶线性时不变系统可用下面的常系数线性差分方程表示［9］:

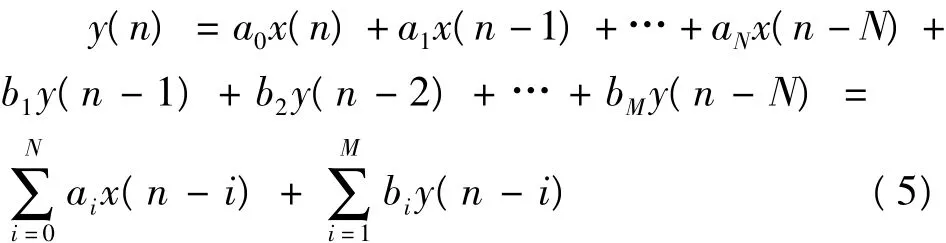
对差分方程进行Z变换为

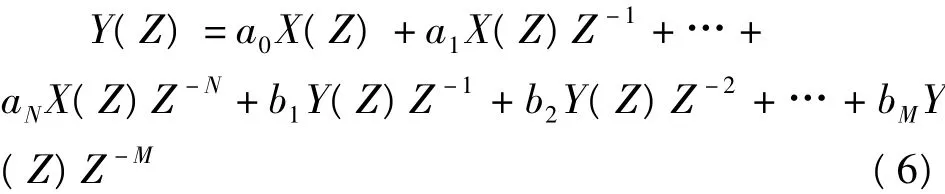
整理后可得:

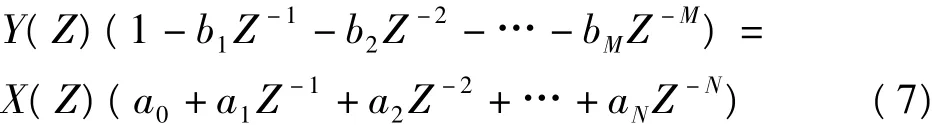
则传递函数为

式中:Ci为滤波器的零点;Di为滤波器的极点。

在设计数字滤波器时，如果希望将某次谐波分量完全滤除，则应对该谐波分量设置为零点，零点应设置在单位圆上，即满足:Ci=ejωTs;如果希望某次谐波分量输出最大，则应将该次谐波分量设置为极点，但极点不能设置在单位圆上。因为如果将极点设置在单位圆上，意味着滤波器对该频率成分的输出为无穷大，这实际上说明滤波器的输出是不稳定的。因此，极点应设置在单位圆内。通常取:Di=RejωTs，R＜1，当 R越接近1，滤波器对极点频率的输出也越大，但滤波器的稳定性会降低［1］。

通过零极点设计的滤波器可以有效的保留所需要的频率成分，有效的滤除高低频的谐波分量。

2.2 狭窄带通滤波算法

我国电力系统输电频率为f=50 Hz，该频率的信号为基频信号，需要保留。通过零极点配置法设计带通滤波算法，保留选定基频信号，抑制非选定频率信号。需要保留的角频率为w=2πf，极点为 D1=RejωTs，D2=RejωTs。同时使幅频特性分别在高低频wT=0和wT=π处完全截止，则设置零点为 C1=ejwT=ej0=1，C2=ejwT=ejπ= －1。根据式 (8)可知传递函数为

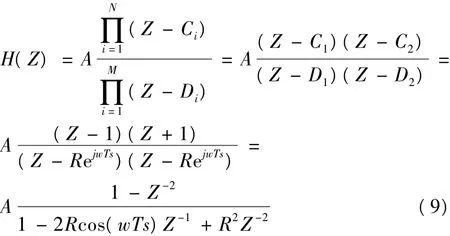
由传递函数可以反推得到狭窄带通滤波算法差分方程:

对于R的取值，本文通过大量数据验证，当R=0.998 7时滤波效果最佳。A的取值与采样频率有关，当一周期采样为200点时，A=796.616 0既采样值被放大了796.616 0倍;当一周期采样为48点时，A=382.954 0。对于A的计算本文有一套精确地计算方案。

当R=0.998 7时，由 (10)式得出的狭窄带通滤波的幅频特性如图2所示。

图2 狭窄带通幅频特性Fig.2 Spectral response of the constrictive band－pass filter

从图2可以看出，在50 Hz附近，幅值响应最大，能够最大限度的保留基频分量，在低频和高频区域，幅值响应较小，对低频和高频分量有较大的抑制作用。所以狭窄带通滤波算法能够有效的滤除低频、高频谐波分量。

2.3 狭窄带通与半波傅里叶结合算法

利用零极点法设置狭窄带通滤波器，可以有效地抑制随机频率分量、衰减直流分量与高次谐波。该滤波器属于IIR滤波器，是一个递推过程。从公式可以看出，只需要3个采样时刻的数据作为输入输出，计算时间窗非常短，但算法的暂态时间会很长。如果初始输入值很接近理论值，则暂态响应时间会大大的缩短，甚至可以直接过渡到稳定状态。利用半波傅里叶算法实部受衰减直流分量影响较小，又可以滤除奇次谐波的优势作为狭窄带通滤波器的初始值计算。可以使得狭窄带通滤波器的暂态响应过程迅速的过渡到稳态状态，提高了继电保护的动作速度性和精确性。

狭窄带通与半波傅里叶算法相结合的步骤如下:

(1)在故障后的第N/2点和N/2+1点进行2次半波傅里叶算法求出其实部X1(N/2)和X2(N/2+1)，得到窄带通滤波算法的输入值。

(2) 令y1=X1(N/2)，y2=X2(N/2+1)。

(3)利用式 (10)计算狭窄带通滤波算法的滤波输出y1，y2，y3，…y(N/2+1)，再利用半波傅里叶算法对其输出进行滤波，得到最终滤波结果。

(4)随着故障点的增多，重复1到3过程。

利用零极法所得的狭窄带通滤波算法与半周波傅里叶算法相互结合，能够有效地抑制非周期分量与谐波分量对半周波傅里叶算法的影响。整个算法对数据窗的需求仅仅是比半周波傅里叶算法多一个数据，即需要数据窗时间为T/2+TS，所需数据量为故障后N/2+1个数据。

3 试验验证

建立故障电流模型来分析狭窄带通半波傅里叶算法的性能，一周期采样点 N=200，R=0.998 7，分别对模型中故障短路电流进行半波傅里叶算法和狭窄带通半波傅里叶算法计算，比较两者的效果。

假设故障电流包含基频分量，2，3，4，5次谐波和衰减直流分量，故障电流生成函数为X(i)=sin(wt+π/6)+0.05sin(2wt+π/3)－

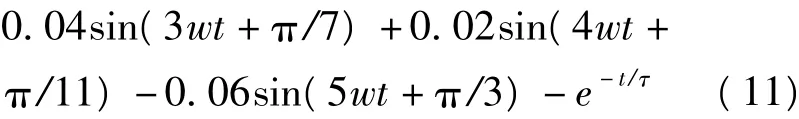
故障电流波形如图3所示。

图3 故障电流波形Fig.3 Fault current waveform

分别对原始数据进行半波傅里叶和狭窄带通半波傅里叶算法进行处理，处理后电流有效值如图4所示。

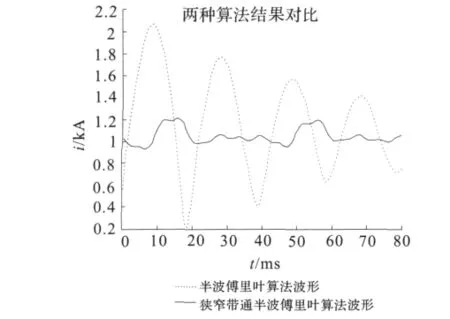
图4 两种算法对比波形Fig.4 Waveform comparison of two algorithms

为了进一步验证算法的可靠性，本文进行了MATLAB仿真实验，采用单侧电源线路故障模型，仿真为220 kV输电线路在0.02 s时发生单相短路接地。

采样数据选用相同时间间隔，即每20 ms采样200个点。发生故障后A相电流变化如图5所示。

图5 A相接地短路前后电流Fig.5 A－phase ground short－circuit current

分别对A相电流数据进行半波傅里叶和狭窄带通半波傅里叶进行处理，电流有效值如图6所示，虚线为采用半波傅里叶算法计算后的波形，实线为采用狭窄带通半波傅里叶算法计算后的波形。

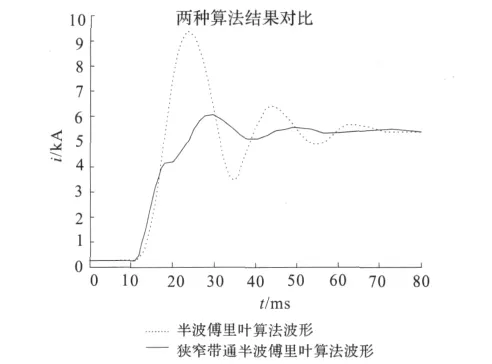
图6 两种算法对比波形Fig.6 Waveform comparison of two algorithms

从图4和图6可以看出，狭窄带通半波傅里叶算法与半波傅里叶算法一样具有快速响应能力。狭窄带通半波傅里叶算法比半波傅里叶算法具有较好的滤波效果，同时对衰减直流分量和低频分量有较好的抑制，受干扰信号影响较小，能够准确的提取基频分量，防止保护误动。本文还通过大量数据验证，在谐波分量较大时，狭窄带通半波傅里叶算法要比半波傅里叶算法更能准确的提取基频分量。

4 结论

狭窄带通半波傅里叶算法时间响应快，所需要的数据窗短。该算法利用狭窄带通对衰减直流分量、低频分量、高频分量和干扰信号的抑制作用，同时利用半波傅里叶算法的快速性、数据窗需求量小特性，快而准确的提取基频分量。能够满足电力系统继电保护速动保护的要求。

［1］张举.微型机继电保护原理 ［Μ］.中国水利水电出版社，2004.

［2］焦彦军，于江涛.衰减直流分量对傅里叶变化快速算法的影响及其消除办法 ［J］.华北电力大学学报，2006(2):62－65.

［3］Alan V O，Ronald W S，John R B.Descrete－time siganal processing ［M］.Prentice－Hall，Inc Copyright，1999.

［4］钱可弥，李常青.电力系统微机保护算法综合性能研究 ［J］.电力系统自动化设备，2005(5):24－26.

［5］Alfuhaid A S，El－Sayed M A.A recursive least－squares digital distance relaying algorithm ［J］，IEEE Trans on Power Delivery，1999，14(4):31－35.

［6］Jeon S J，Cho G H.A series－parallel compensate ed uninterruptible power supply with sinusoidal input current and sinusoidal output voltage［C］//In Proceedings of the 28thAnnual IEEE Power Electronics Specialists Conference，Vol.1.PESC St Louis，CA ，USA:1997.297－303.

［7］孙雅明，张兆宁，史艳红.电力系统故障暂态信号中提取基波分量的短窗积分算法 ［J］.电力系统自动化 ［J］，2000，6(2):30－33.

［8］熊岗，陈陈.一种能滤除直流分量的交流采样新算法［J］.电力系统自动化，1997，21(2).

［9］李庚银，陈志业，杨峰.电力系统暂态波形分析方法［J］.中国电机工程学报，1995，15(3):204－209.