传感器网络的粒子群优化定位算法

陈志奎， 司 威

（大连理工大学 软件学院，辽宁 大连 116023）

0 引言

随着物联网研究和应用的深入，由信息采集层和信息传输层构成的信息感知体系是物联网应用推进的主要领域，而无线传感器网络行业在其中起到关键的推动作用。无线传感器网络是一个多跳自组织网络系统，传感器节点之间协作地感知、采集和处理网络覆盖区域中感知对象的信息，并通过传感器网络发送给需求者。无线传感器网络由于具有远程监控、实时监测并且能在恶劣或特殊环境工作等诸多优点而被广泛应用于智能交通、国防军事、环境监测、医疗卫生、空间探索、精细农业等诸多领域[1-3]，其中节点定位技术则是无线传感器网络进行目标识别、监控、跟踪等众多应用的前提。

定位技术是无线传感器网络的主要支撑技术之一。获取传感器节点的位置信息是传感器网络应用的一种重要部分，在传感器网络执行监测活动时，事件发生的位置和观测节点的位置信息往往是传感器节点采集数据中不可缺少的部分，没有位置信息，网络所获得的数据将毫无意义。

无线传感器网络定位可分为基于测距的定位和无需测距的定位算法，其主要区别在于是否需要距离信息。基于测距的定位算法中节点使用测距技术获得距离信息，定位精度较高但是需要额外的设备，其中常用的测距技术有接收信号强度RSSI[4]，信号到达时间TOA[5]，信号到达时间差 TDOA[6]和信号到达角度 AOA[7]等；而无需测距的定位算法仅依靠相邻节点间的连通关系进行定位，无需基础网络设施的支持，定位精度较低。

由于传统的节点定位算法采用最小二乘法求解非线性方程组很容易受到测距误差的影响。为了提高节点的定位精度，将粒子群优化算法引入到无线传感器网络定位中，通过迭代算法寻求最优解，有效抑制了测距误差的累积对定位精度的影响，而且该算法需要的锚节点个数相对较少，一定程度地降低了网络费用。

1 传感器网络的粒子群优化定位算法

1.1 粒子群优化算法

粒子群优化算法是基于群体智能理论的一种新兴演化计算技术，通过个体间的协作与竞争，实现复杂空间中最优解的搜索。

粒子群优化算法数学模型描述为：假设粒子群的群体规模为 S,其中在 d维搜索空间中第 i个粒子的位置和速度可以分别表示为通过适应度函数，确定t时刻每个粒子所经过的最佳位置以及群体所发现的最佳位置Pg,再按照如下公式分别更新粒子的速度和位置[8]：其中，w为惯性因， c1和 c2为正的加速常数， r1和 r2为[0,1]间均匀分布的随机数。假设粒子的最大速度为 vmax，则粒子的速度通常设为每维变换范围的10%～20%[9]。

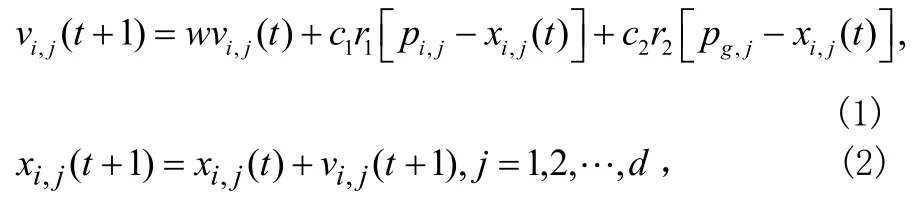
1.2 惯性权重

惯性权重 w的大小决定了粒子对当前速度继承的多少，通过权重 w可有效控制算法的搜索能力和挖掘能力。若 w取值较大，则粒子的全局搜索能力较强，有利于粒子跳出局部极小点；若 w取值较小，则粒子的局部挖掘能力较强，有利于算法收敛。文献[10]通过实验证明，w的取值随着算法迭代而线性减小时，算法具有较强的收敛性。

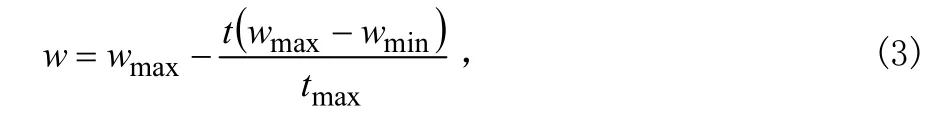
其中，maxw 和minw 分别是初始和终止惯性权重，t是当前迭代次数，maxt 是最大迭代次数。

1.3 适应度函数计算

适应度函数用来评价各个粒子在种群中达到或接近于最优解的优劣程度，从中选出每个粒子的个体极值和种群的全局极值。

假设二维空间中有 M个锚节点，N个未知节点。已知M个锚节点的坐标 AI( xi, yi),i = 1 ,2,… ,M ,未知节点到锚节点的距离 di,i = 1 ,2,… ,M ，则未知节点坐标(x , y )满足公式(4)：

由于存在测距误差、环境因素等影响，测量距离总存在一定误差使上述公式不能全部成立。假设 fi,i = 1 ,2,…,M为未知节点到锚节点之间的测距误差值，则 fi满足：

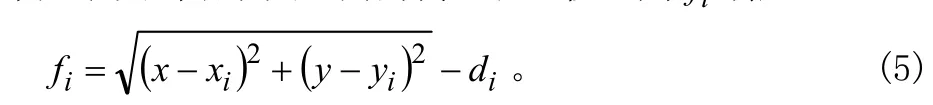
无线传感器网络定位中，测距误差值 fi越小，定位结果越精确。因此适应度函数定义为：

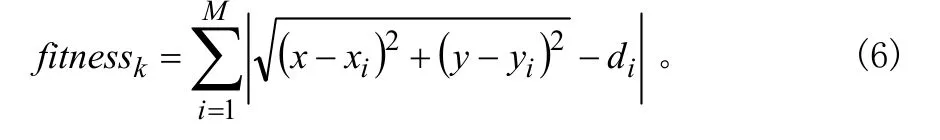
1.4 粒子保活性

粒子群优化算法的寻优能力主要依赖粒子之间的相互作用和相互影响，而粒子自身没有变异能力。这表明当单个粒子陷入局部极值时可以通过借助其它粒子来逃逸局部极值点；但当大部分粒子均被相同的局部极值所限制时，整个算法就会进展缓慢，甚至出现停滞现象。

为了保持粒子的活性[11]，首先，判断粒子是否失活（失活指在迭代过程中连续一定代数粒子的适应值都没有优于历史最优的适应值），若粒子失活，则对失活粒子进行变异，即要么使粒子以较小的变异概率在其迭代过程中获得的维空间内重新初始化；要么使粒子在其当前位置进行扰动，并将变异或扰动的结果无条件地接受为当前粒子的历史最优。以此来增强全局搜索能力,克服粒子群陷入局部解的缺点，同时又可以加快收敛速度、提高搜索精度。

1.5 传感器网络的粒子群优化定位算法

传感器网络的粒子群优化定位算法流程如下：

①初始化所有粒子，群体规模为 S。在部署区域内随机初始粒子的位置和速度，计算每个粒子的适应度值，选择适应度值最小的粒子位置初始化为全局极值，其它粒子的适应值初始化为粒子的个体极值，然后转向步骤⑥；

② 根据式(6)计算每个粒子的适应度值；

③ 对每个粒子，将其当前的适应度值与其历史最优位置所对应的适应度值进行比较，如果当前粒子的适应度值小于历史最优位置所对应的适应度值，则用粒子当前位置更新粒子最优位置，否则判断粒子是否失活（即粒子在一定迭代次数内都没有取得好于粒子最优位置的适应度值），若失活则粒子进行变异，保持粒子活性，否则执行步骤④；

④ 对每个粒子，将其当前最优位置对应的适应度值与群体历史最优位置对应的适应度值进行比较，如果当前粒子的适应度值小于群体历史最优位置所对应的适应度值，则将粒子当前位置作为群体最优位置；

⑤ 检查终止条件（达到最大迭代次数或者适应度值在测距误差范围内）。若终止条件满足，转向步骤⑦，否则转向步骤⑥。

⑥ 根据式（1）和式（2）更新粒子的速度和位置，转向步骤②；

⑦ 输出全局极值对应的粒子位置，退出循环。

2 仿真实验

2.1 仿真环境设置

使用 MATLAB对传感器网络的粒子群优化定位算法进行仿真，仿真过程中，节点随机分布在一个无障碍的 100 m×100 m的正方形区域内，其中网络规模为 100，锚节点比例为10%，节点的无限射程40 m。种群规模S=20，最大迭代次数 tmax=50，最大速度 vmax=10,初始惯性权重wmax=0.9，终止惯性权重 wmin=0.2，c1=c2=2。

2.2 仿真结果分析

仿真实验主要分析了锚节点密度、网络连通度、测距误差对节点定位的影响，并与最小二乘法进行比较分析。

锚节点密度反映了每个未知节点周围的锚节点个数。图 1描述了锚节点密度对平均定位误差的影响。由于锚节点本身的成本较高，因而锚节点的密度将直接影响网络的整体成本。由下图可知，随着锚节点密度的增加，平均定位误差将逐渐下降，但当锚节点密度达到 10%时，平均定位误差下降速度缓慢，因而粒子群优化的定位算法对锚节点的密度要求不是很高，在锚节点密度相对较小时，也能达到很好的定位效果。

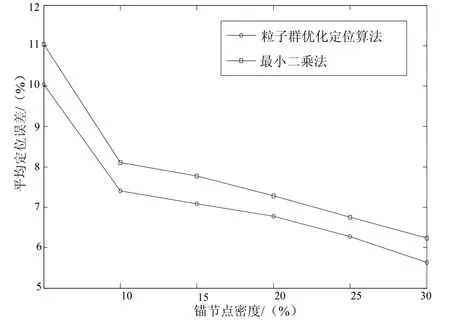
图1 锚节点密度对平均定位误差的影响

网络连通度反映了能相互通信的节点间的通信量，在仿真过程中可以通过改变节点的无线射程来改变网络的连通度。图 2显示了网络连通度对平均定位误差的影响，由图可知，随着网络连通度的增大，节点的平均定位误差变化相对缓慢，说明粒子群优化的定位算法对未知节点间通信量要求不大，定位节点的能耗较小。

测距误差直接影响距离测量值的准确度。图 3显示了平均定位误差随测距误差变化的情况，由图可知，随着测距误差的增大，平均定位误差也逐渐增大，但粒子群优化的定位算法有更小的定位误差，达到较高的定位精度。

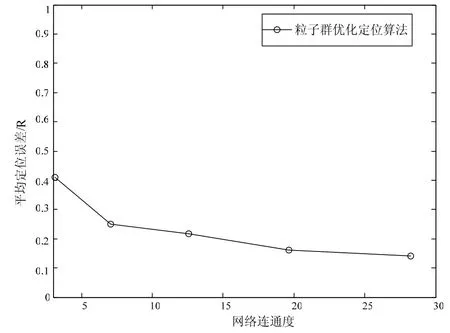
图2 网络连通度对平均定位误差的影响

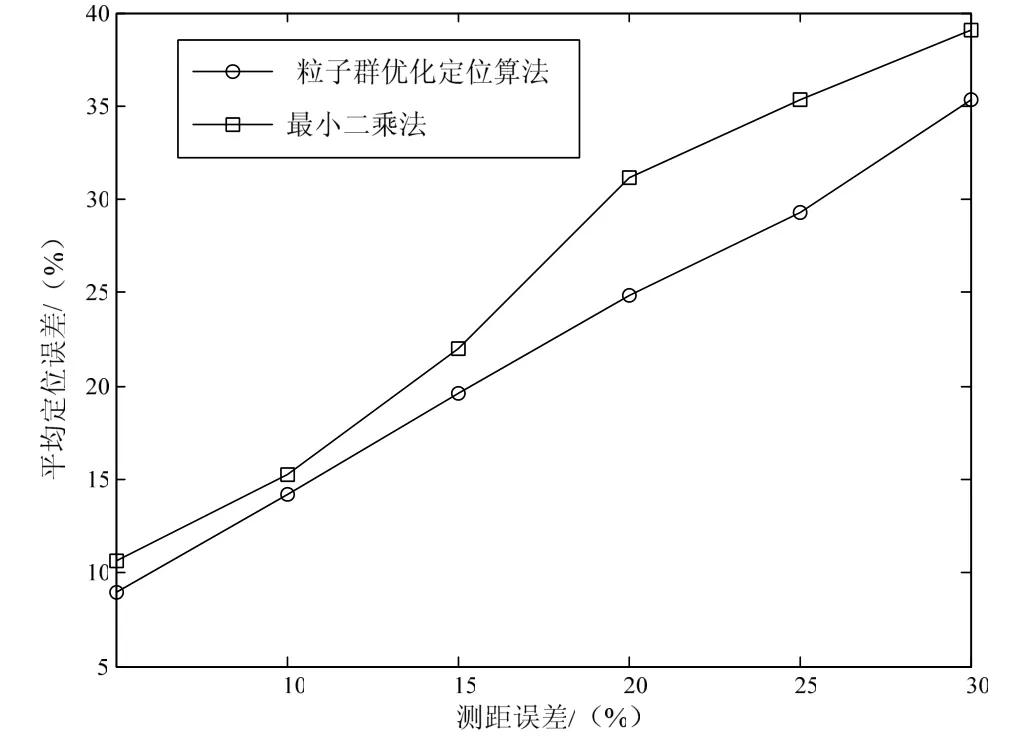
图3 测距误差对平均定位误差的影响

3 结语

粒子群优化的传感器网络定位算法通过采用迭代的方式搜索节点的位置。仿真结果表明：粒子群优化的定位算法有效地提高节点的定位精度，尤其在测距误差较大的情况大具有较好的定位效果，适用于无线传感器网络定位。然而，该算法仍然存在一些不足，下一阶段的工作是考虑算法的能耗，进一步改进算法提高算法的稳定性及定位精度。

[1] 郑丹玲,董宏成.无线传感器网络与其关键技术[J].通信技术,2008，41(08)：179-197.

[2] 范波,苗伟.无线传感器网络及其在环境监测应用概况[J].通信技术,2009,42(12)：170-172.

[3] 明光照, 李鸥, 张延军. 基于无线传感器网络的职能家居系统设计[J]. 通信技术, 2009,42(02)：233-237.

[4] DOHERTY L, PISTER K S J, E I GHAOUI L. Convex Position Estimation in Wireless Sensor Networks[C]NJ： IEEE, 2001：1655-1663.

[5] GRIOD L, ESTRIN D. Robust Range Estimation Using Acoustic and Multimodal Sensing[C]. USA： IEEE Computer Society,2001：1312-1320.

[6] SAVVIDES A, HAN C C, STRIVASTAVA M B. Dynamic Fine-grained Localization in Ad-hoc Networks of Sensors [C]New York： ACM Press, 2001： 166-179.

[7] NICULESC D, NATH B. Ad Hoc Positioning Systems(APS) Using AOA[J].In：Proc. of the IEEE INFOCOM 2003, 2003(03)：1734-1743.

[8] SHI Y,EBERHART R C.A Modified Particle Swarm Optimizer[C]. USA：IEEE,1998：69-73.

[9] EBERHART R,SHI Y H. Particle Swarm Optimization： Developments,Applications and Resources[C].USA：IEEE, 2001： 81-86.

[10] BERGH F,ENGELBRECHT A P.A Cooperative Approach to Particle Swarm Optimization[J]. IEEE Trans. on Evolutionary Computation, 2004, 8(03)： 225-239.

[11] 卢克中,王汝传,帅小应.保持活性的改进粒子群优化算法[J].计算机工程与应用,2007,43(11)：16-38.