基于矩阵二阶矩和小波分解的紊流图像融合灰色关联度评价*

梁忠伟，叶邦彦，刘晓初，萧仲敏

(1.华南理工大学a.机械与汽车工程学院;b.国家金属材料近净成形工程技术研究中心，广州 510640;2.广州大学机械与电气工程学院，广州 510006)

基于矩阵二阶矩和小波分解的紊流图像融合灰色关联度评价*

梁忠伟1，2，叶邦彦1a，刘晓初2，萧仲敏2

(1.华南理工大学a.机械与汽车工程学院;b.国家金属材料近净成形工程技术研究中心，广州 510640;2.广州大学机械与电气工程学院，广州 510006)

在引入多尺度小波分析的基础上，通过对紊流图像进行多尺度小波分解，建立小波系数矩阵二阶矩以标识对应部分的图像清晰度，通过特定选择机制进行图像重建，最终获得清晰的图像融合结果。选取紊流图像特征建立参数数据组，构建灰色评价数学模型，计算各图像特征之间的灰色关联度，得出了研究结论与参考建议。该实验使紊流图像的细节和缺陷等能够得到很好的展现，为图像融合关联度的监控和调试提供了理论基础和技术准备。

二阶矩;小波分解;图像融合;灰色关联度;评价

0 引言

图像融合是通过特定的算法将多个相关图像数据结合在一起生成一个新的图像［1］。由此图像的各个部分可以得到清晰的展现，部分以及斑点能得以去除，并提高图像信息的可用程度，同时增加对研究对象解释的可靠性。目前研究人员取得了许多研究成果。但由于很多研究都是采用普通的小波分析结果以重建图像，难以获得高清晰度的图像。在引入多尺度小波分析的基础上，通过对图像各个部分进行多阶小波分析，建立小波系数矩阵二阶矩以标识对应相关部分的图像信息的清晰度，并通过灰色关联度对图像效果进行评价。

1 融合算法分析

1.1 图像频率域的多尺度小波分解

将数字图像看作为二维数字信号，则图像空间L2(R)变为二维空间L2(R×R)，而二维尺度函数变为f(x，y)。考虑函数是可分离的情况:

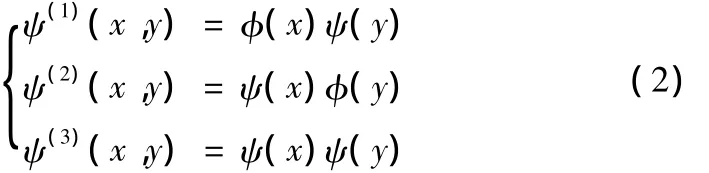
随后对于图像进行正变换，将图像f(x，y)分别与各个小波基图像进行内积，再在x和y方向进行2倍间隔抽样生成多分辨率小波频域分解图像序列［3］。如下式所示:

如此反复进行直至最终获得图像清晰度逐渐降低的小波分解系数矩阵序列

1.2 小波系数矩阵二阶中心矩的建立

二阶矩反映了系数矩阵内部各个元素数值以及各个方向上系数变化频率分量在数量上的分散程度。如二阶矩数值越大，则说明其内部系数分布越分散，则可获得更为清晰稳定，轮廓分明的图像外观效果;反之则说明其系数分布越为集中与相近，则获得边界的图像外观效果。小波系数矩阵二阶中心矩定义如下式［4］:

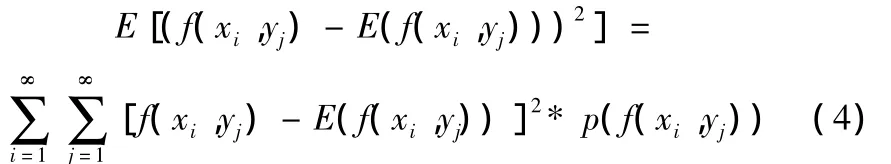
其中:f(xi，yj)为小波系数矩阵元素数值;E(f(xi，yj))为小波系数矩阵值的数学期望;P(f(xi，yj))为系数矩阵元素f(xi，yj)出现概率。

图像小波系数矩阵元素分布呈正态分布并在二维方向上相互独立，由此可根据概率分布独立性准则分别进行单维方向正态分布分析［5］:

p(xi)与p(yj)分别为x，y方向矩阵元素值出现概率。因此可分别求取小波系数矩阵数值在该坐标轴方向上出现概率的数学期望E(x)，E(y)［6-7］:

则E(x，y)可求得:

将(5)，(6)和(7)式分别代回(4)式，可推导出小波系数矩阵二阶矩计算公式为:

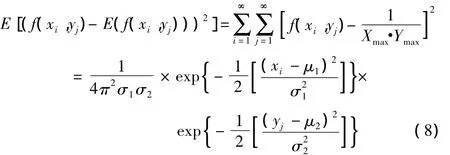
其中各变量含义同前。

2 灰色理论模型

在具体实验中往往只能获取部分数据，且其往往介于所谓的有影响和无影响之间，即系统的性［7］.设灰色系统参数序列为［8］:

逐个计算被评价对象指标序列与参考序列对应元素的绝对差值即:

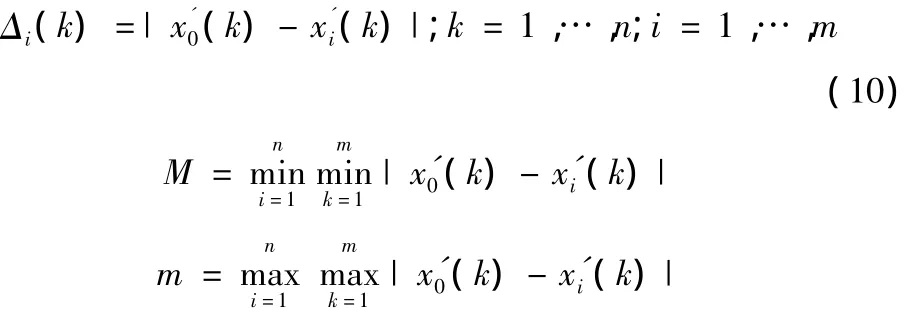
计算评价与参考序列元素的关联系数［9-10］:

式中ξ为分辨系数，ξ越小，关联系数间的差异越大，区分能力越强。通常ξ取0.5。

对所求得的n个关联度进行规范化处理，即可得到各个特征值的相对权重［11］:

根据灰色关联度及相对权重，得到［12］:

式中:p为Minkowski距离，且j=1，2，…，12;k=1，2，…，7。若rik越大，表明目标图像特征值xi与第k类影响因素关联越接近［13-14］。

3 实验与评价

实验在封闭壳体内进行，封闭空间长1m，宽0.8m，深0.6m，试验时采用水基强化液，其在封闭空间内深度达到0.5m。试验雷诺数Re=uh/v经测定为4700。硬件条件为:处理器为 Celeron 2.26，内存256M，软件平台为 MATLAB 7.0操作系统为Windows XP。获得待处理图像Ai与Bi并进行子图像划分，分别依次将待处理图像Ai与Bi等分成Mi×Ni幅子图像，成为子图像集 Ai，m，n与 Bi，m，n。

通过对两个二维图像 Ai，m，n与 Bi，m，n进行 N 层小波分解，最终其分别将有(3N+1)个不同的频带，之后针对各个子图像所求得的小波系数矩阵求取二阶中心矩，并以此作为标识该小波系数矩阵的图像清晰度与分布分散度特征参数;

选取相应坐标位置的两幅矩阵图像进行二阶中心矩的差值对比，如其差值小于预定阈值δ，则说明图像的清晰度较接近，为避免损失图像细节，则对该两幅图像矩阵进行数值平均处理;

其中，GLHi(x，y)为处理后的小波系数矩阵图像;ALHi(x，y)与 BLHi(x，y)为特定坐标位置(x，y)的相应两幅第i个分解层次上的小波系数矩阵图像;E(ALHi(x，y))与E(BLHi(x，y))为该相应两幅小波系数矩阵图像的二阶中心矩;δ为预定的二阶中心矩差值阈值，将是否处于样本数值总数的99.73%作为标准正态分布样本有效划分准则:

如二阶中心矩大于预定阈值δ，则:

而对于ALLi(x，y)与BLLi(x，y)，选取二阶矩数值较小而低频分量较弱的的小波图像系数矩阵供后续技术处理，如下式所示:

对组合后的图像矩阵进行连接，组成统一的整体图像系数矩阵。通过二维小波逆向变换，得到融合后的芯片整体融合图像。图像融合过程如图1所示。

图1 紊流图像融合过程

根据公式(1)～(3)建立评价数值序列并列举主要图像特征(根据紊流特点选取图像能量、信息熵、图像惯性矩、平稳度、图像方差、能量分布系数、Zernike矩、信噪比及对比度等图像特征［15］)，如表2所示。参照公式(9)～(12)进行确定灰色系统的相对权重，根据公式(13)在图像一级、二级及三级小波分解阶次条件下进行图像低频部分特征间的灰色关联度确定，如表3所示。可以看出:弹性变化率与平稳性、信噪比、对比度等特征量关联度较大;能量离散率将影响图像信息量的均衡分布;外载荷修正量的增加将使得图像特征得以更为清晰的显示，但是同时导致图像信息其受外界干扰机率也随之增加;曲面Zernike矩使得图像抵御光学变形能力逐渐增强;光顺误差将严重降低图像质量。

表1 子图像多小波分辨率二阶矩比较

表2 图像样本特征值

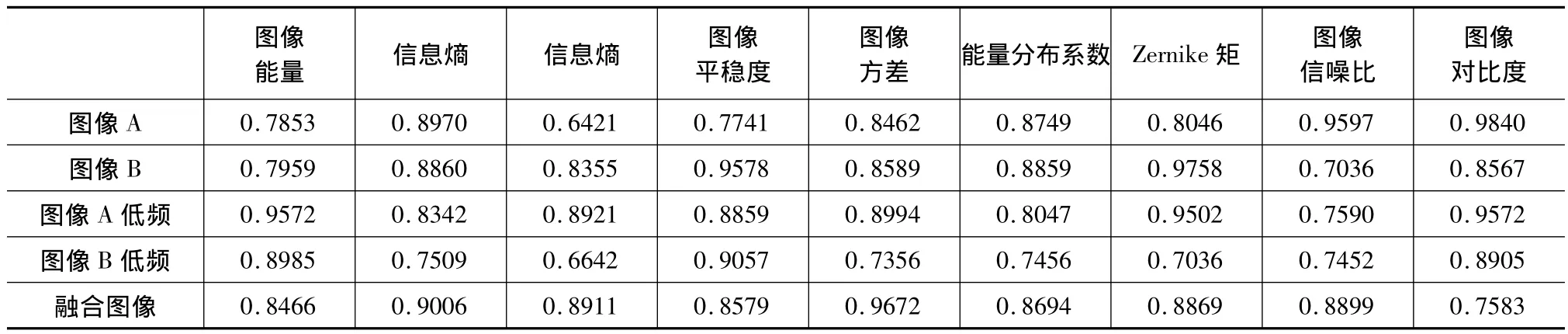
表3 紊流图像融合灰色关联度

4 结束语

进行了基于小波系数矩阵二阶矩和多尺度小波分析的紊流图像融合灰色关联度评价。首先对待处理图像进行多阶二维小波分解求得小波系数矩阵集合，选择出图像清晰、信息丰富的小波系数矩阵集合并进行图像系数矩阵组合后，对其进行逆向小波变换以重建出稳定清晰的整体芯片图像，之后在图像特征与形貌影响因素间进行灰色关联度的计算，并对影响进行了评价，量化定义了其变化规律。成功解决了在传统紊流分析中无法进行图像定量评价的难题。为紊流图像检测提出了新的思路。

［1］ZHU H.Foundation of Digital Image Processing［M］.Beijing:Press of Science，2005:246-267.

［2］SONG Chun-lin，FENG Rui，LIU Fu-qiang，CHEN Xi.A novel fractal wavelet image compression approach［J］.Journal of china university of mining ＆ technology.2007，3(17):121-125.

［3］TAO Bing-jie，WANG Jing-ru，XU Jun-ping.Study on Image Fusion Based on Different Fusion Rules of Wavelet Transform ［J］.Infrared Technology.2006，28(7):431-434.

［4］CHU Heng，ZHU Wei-le.Image fusion algorithms using discrete cosine transform ［J］.Optics and precision engineering.2006，14(2):266-273.

［5］H Zhu，J Zhou，H Li.3D barcode preprocessing scheme based on image recognition［J］.SPIE.2002，4875:651-655.

［6］Zhao J，Pan J S，Chen G H.Study on application of combination of wavelet with fractal in image processing［J］.Computer Engineering，2005，31(1):29-32.

［7］S.LZHU，Taleb-Ahmed A.Applying the Hough transform pseudo-linearity property to improve computing speed［J］.Pattern Recognition Letters，2006，27(16):1893-1904.

［8］LIAO Shi-zhong，GAO Pei-huan，SU Yi.Amending method of image geometric distortion in optical-lens vidicon［J］.Journal of Image and Graphics，2006，24(7):593-596.

［9］LI Guo-Ping，Cui Cheng-song，Chen San-ben，etal.A fast sub-pixel edge detection method using Sobel-Zernike moments operator［J］.Image and Vision Computing，2007，3(1):11-17.

［10］LI De-hua，etal.Analysis and rectification of kinematic error in high-definition image acquisition system［J］.Computer and Digital Engineering.2004，23(6):37-40.

［11］ZHU Hong-de，LOU Xiao-ping，DENG Wen-yi，LV Naiguang.Meta-graph recognition and measurement in 2-D machine vision ［J］.Computer Engineering and Applications，2006，11(3):217-218.

［12］WANG Yue-zong，etal.Recognition of target object in Micro-image［J］.Computer Engineering and Applications，2003，25(9):98-100.

［13］Song Chun-lin，Feng Rui，Liu Fu-qiang，etal.A novel fractal wavelet image compression approach ［J］.Journal of China University of Mining＆ Technology:English edition，2007，17(3):121-125.

［14］WANG Lijuan，RU I Yannian，JIANG Xiaomei.The quality evaluation methods for chip package based on the theory grey［J］.Machine Design and Research.2008，24(6):91-94.

［15］Kun Liwen.Weighted Grey Relation Grade［J］.Journal of Grey Systems，2005，23(4):27-29.

Evaluation of Gray Relational Degree of Turbulence Image Fusing Based on Matrix Quadratic Moment and Wavelet Decomposition

LIANG Zhong-wei1，2，YE Bang-yan1a，LIU Xiao-chu2，XIAO Zhong-min2
(1a.School of Mechanical＆Automotive Engineering;b.National Engineering Research Center of Near-Net-Shape Forming for Metallic Materials，South China University of Technology，Guangzhou 510640，China;2.School of Mechanical＆ Electrical Engineering，Guangzhou University，Guangzhou 510006，China)

On the basis of introducing the technology of multi-scale wavelet analyze,turbulence images are wavelet decomposed,quadratic moment of corresponding image’s wavelet coefficients is used to identify the definition of image.Thus the required image definition is gotten by wavelet reverse analyzing and reconstructing of image with a specific selecting criteria.After selecting different image characteristics and establishing its parameter-array,a mathematical model of gray evaluating system is structured.After calculating the gray relational degree of the image characteristics,thus the research conclusions and referential suggestions are reached.It provides a clear turbulence image which identifies its detail and defect effectively,the theoretical foundation and technical preparation can be provided for the monitoring and adjusting of image fusion’s relational degree.

quadratic moment;wavelet decomposition;image fusion;gray relational degree;evaluation

TP391.4

A

1001-2265(2011)08-0001-04

2011-01-04

国家自然科学基金项目(50875059);国家自然科学基金项目(50875052);广东省高校优秀青年创新人才培育项目(LYM09110);广州市属高校科研项目(10A068);广州大学新苗计划(LZW2-2091)

梁忠伟(1978—)，男，广州人，副教授，博士后，主要研究方向为机器视觉、图像处理、自由曲线曲面建模等，(E-mail)lzwstalin@126.com。

(编辑 李秀敏)