用等效地层损失理论计算隧道沉降

1 引言

一般认为，隧道开挖引起的地面沉降主要是地层的损失引起的。Peck(1969)在对很多的实测数据进行分析后提出了一种经验计算方法，该方法认为地面沉降的分布服从高斯分布。在其后，O’Reilly和News(1982)[1]、Loganathan和Poulos(1998)[2]、Attewell(1974)等[3]、姜忻良（2004）[4]和魏纲（2007）[5]等许多国内外学者针对不同的影响因素对Peck的计算方法提出了修正。韩煊（2007）[6]对Peck公式在我国的适用性进行了分析。Peck公式在隧道开挖引起的地面沉降预测中收到良好的效果。但是，应该指出的是当年Peck提出该经验公式只是无法解释地面沉降分布的权宜之计，在具体工程实例中，沉降槽宽度系数的确定大多依靠经验，预测的准确性无法得到保证。因此，应该分析地层损失造成沉降的机理，并在其基础上提出计算的方法。本文基于等效地层损失法提出了理论计算方法，以期能在理论上揭示地层损失造成地面沉降的机理。

2 理论推导

2.1 等效地层损失理论

由隧道开挖引起的地面沉降取决于三个因素（Rowe,1986）[7]：（1）施工场地的地质条件和地下水流条件；（2）隧道埋深和直径；（3）施工过程中的影响。以上因素通过地层损失量对地面沉降有不同程度的影响，传统的经验方法基于观测数据，而Lo和Rowe(1982)[8]、Rowe和Kack(1983)[9]提出了一种等效地层损失法的理论计算方法，该方法的基础是地层损失参数。隧道变形的模式如图1所示，图中的参数g即为地层损失参数。其表达式如下：

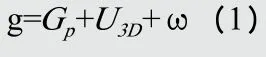
图1 隧道横断面周围的土体变形模式

式中，Gp为掘进机与管线之间的空隙，U3D为掘进机前部土体的三维弹塑性变形，ω为施工因素造成的地层损失。

Lee(1992)[10]对（1）式中各个参数的确定方式进行了描述，具体如下：

（1）Gp的确定

式中，Δ为掘进机页片的厚度，δ为安装管线所需要的净空。Ingle(1972)指出水泥和土的混合物随时间缩短7%～10%，因此，如果考虑到注浆的影响，则（2）变为：

（2）U3D的确定

隧道的开挖造成了隧道顶部土体应力状态的改变，土体向隧道内移动，侵入隧道的土体在开挖过程中被立即清除。这部分土体的损失量为：

式中，k为土体的剪切阻力因数，δx为土体侵入隧道量。k的取值一般为0.7～0.9。

式中，Ω为无量纲变形因数，R为隧道半径，E为弹性模量，P0=K'0P'v+Pw-Pi，K'0为有效静止土压力系数，P'v为隧道管线竖向有效应力，Pw为隧道管线孔隙水压力，Pi为隧道支护压力。

（3）ω的确定

式中，ui为隧道顶部的弹塑性变形。

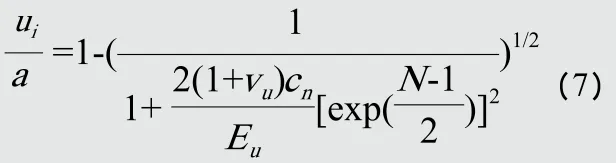
地层损失是引起地面沉降的主要原因之一，在Lee(1992)的理论中将地层损失量的许多影响因素，诸如，注浆、隧道管线的偏移、隧道埋深和人为因素造成的地层损失都考虑在内，在理论上揭示了造成地层损失的原因。Loganathan和Poulos(1998)将等效地层损失理论与Verruijt(1996)[11]的理论相结合来计算地面沉降的分布规律，许多参数还是靠经验确定。

2.2 对应等效地层缺失理论

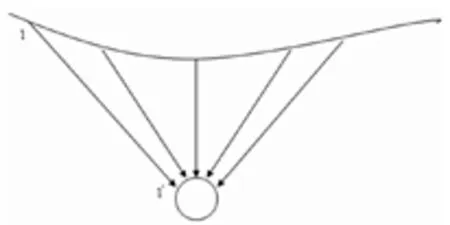
图2 隧道周围土体变形示意图

为了在理论上揭示地面沉降的分布，本文在Lee(1992)的基础上提出了对应等效地层缺失理论。由于在地下某点的土层缺损造成地面上的点都向该点运动，图2 所示，地面上的点位移都指向隧道的轴心，这些位移的竖向分量便是该地面点的沉降量。1点的沉降是由于1'点的地层损失引起的，即两点是对应的。利用等效地层损失理论可以求得1'点的地层损失量，再利用1点和1'点之间的对应关系求1点的沉降，即为本文的对应等效地层损失理论。

如图3所示在隧道横截面内建立径向坐标系，假设a'的地层损失参数为ga'，则a 点的沉降量为：

a点距隧道中心的水平距离为：

式中，H为隧道的埋深，r为隧道的半径。

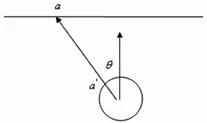
图3 横截面径向坐标系

3 算例

3.1 伦敦希斯罗机场高速公路隧道

希斯罗机场高速公路隧道总长8千米，隧道直径8.5米，隧道轴心距地面19米。Loganathan和Poulos(1998)利用等效地层损失理论计算的地层损失率为1.36%，假设隧道横截面的形式为图1（a），则隧道周围的地层损失参数为3.2cm。利用本文算法对其进行地面沉降预测结果如图4。

3.2 加拿大萨德湾隧道

萨德湾隧道位于加拿大萨德湾市，全长3.3千米，隧道直径2.47米，隧道埋深10米。具体的隧道地质条件见Lee(1992)。利用等效地层损失理论计算的地层损失率为14%，隧道周围的地层损失参数为2.1cm。利用本文的算法预测的地面沉降如图5所示。

3.3 计算结果分析

由图4、图5可见，本文的计算方法是可靠的。但是需要指出的是在距离隧道中心较远的地方，本文的计算值与实测值相比较大，这主要是因为本文为了计算的简便假定隧道周围土体的变形模式为图1（a），而大部分隧道的变形模式为图1（b），明显可以看出后者距隧道中心越远，地层损失参数越小，因此沉降量应比用前者计算的小，也就跟实测值更接近。

4 讨论

Peck公式沿用至今，经过许多学者针对不同地区隧道的修正已经形成了一个体系，在隧道地面沉降预测中取得满意的效果。但是，我们应该看到其也存在着参数确定主要依靠经验的问题，不同的预测值得到不同的预测结果，这给指导工程实际应用造成了一定的困难。Rowe、Lee等学者在分析影响地层损失的不同因素后提出的等效地层损失理论在理论上揭示了地层损失发生的原因，避免了过多依靠经验进行计算的问题。本文正是利用了等效地层损失理论的这一优点。

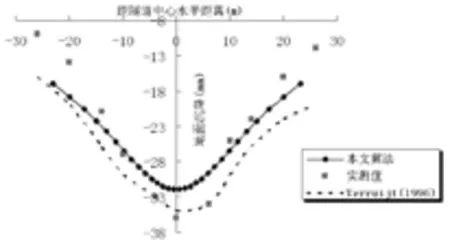
图4 希斯罗机场高速公路隧道地面沉降预测

5 结论

本文以等效地层损失理论为基础，提出了一种简单的预测隧道地面沉降的方法，该方法能考虑造成地层损失的各个不同因素的影响。作者认为造成地面点沉降的原因是地面点朝向隧道中心的运动，因此地面点的沉降是由于隧道顶部的对应点的地层损失造成的。经过对两个算例的计算得到了较好的预测效果。

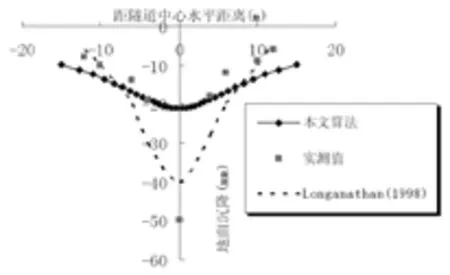
图5 萨德湾隧道地面沉降预测