淤堵试验中“驼峰”形 k～t曲线形成的影响因素分析

付长生,赵 坚,沈振中,杭学军,张 松

(1.河海大学水利水电学院,江苏 南京 210098;2.江苏省交通规划设计院股份有限公司,江苏 南京 210005;3.扬州市勘测设计研究院有限公司,江苏 扬州 225009)

工程实例表明,作为反滤材料的土工织物若选择不当,使用过程中容易产生淤堵,影响反滤效果。为保证土工织物的反滤效果稳定、持续、有效,可以通过土工织物与被保护土的淤堵试验对土工织物进行选型。笔者通过分析多组土工织物淤堵试验所获得的渗透系数(k)与时间(t)的关系曲线发现,在淤堵试验初始阶段,存在明显的 “驼峰”形k～t关系(图1),即包含被保护土和土工织物的透水体的渗透系数在试验初期随时间逐渐增大,经过一段时间到达峰值后逐渐减小并趋于某一固定值。文献[1-2]对淤堵试验的“驼峰”现象有过描述,但只作了简单解释,未见深入分析。笔者将以试验为基础,通过多因素综合分析,探讨“驼峰”产生的原因,分析影响k～t曲线峰值kmax、峰值出现时间T1和持续时间T2的主要因素及其敏感性。

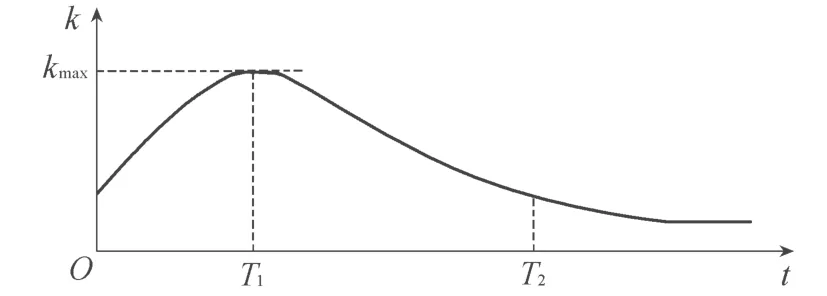
图1 k～t曲线

1 试验模型及试验方案

1.1 试验原理

淤堵的过程是渗透系数逐渐变化并最终趋于某一定值的过程,本质上是渗透变形的一种特殊情况。因此,可以参照达西渗透试验原理设计土柱模型进行室内淤堵试验。

1.2 试验模型

土柱模型试验是土工织物淤堵试验研究中最常用的方法,也是最简单有效的方法。笔者采用此方法,利用循环水测试系统分别采用短筒及改进的长筒模型进行室内模型试验。

短筒模型参照SL 237—1999《土工试验规程》中常水头70型渗透仪的原理制作而成,一般试验土样高度为8cm。改进长筒模型是在文献[3]推荐的长筒模型基础上,针对本文研究需要加长试验筒柱并沿筒柱增设测压管口(间隔25mm)。改进的模型筒由模型筒身、有机玻璃盖、钢筋吊紧螺栓等部分组成,筒身直径为10 cm,高度为80 cm,模型筒身选用有机玻璃制作。改进的长筒模型示意图见图2。

图2 改进的长筒模型示意图

1.3 试验流程

试验时,按不同干密度、颗粒级配及细粒质量分数拌制土样,并装填到模型筒中,在土样出水端铺垫选定的土工织物。模型筒试样从上到下分别为砾石层、粗砂层、土样(改进长筒模型中土样高度为20cm,分别标记Ⅰ～Ⅷ层)、土工织物、粗砂层、砾石层。进水方式自上而下。装样完成后,进行土样饱和及排气程序。饱和排气时由模型筒下部进水,需控制水头缓慢增加,直至饱和排气完成。此过程一般耗时较长,约24h以上,饱和过程中气泡由下至上冒出,经上部排气阀排出。随后,逐步增加水头至合适值,观察测压管水头高度,维持稳定后开始测试,主要测量各观察点测压管水头高度和试样过水流量,并计算对应的渗透系数。当所测试样渗透系数随时间趋于一个稳定值时,试验结束。

1.4 试验方案

初期试验及相关文献表明,影响淤堵试验渗透系数“驼峰”形态的因素主要是外荷载、土工织物及土体三大类,本文据此选用水头、土工织物单位面积质量、细粒质量分数、颗粒级配和干密度5个因素。用正交试验方法,选择 L18(21×37)正交表,设计了18组典型试验工况来研究多因素对k～t曲线“驼峰”形态的影响。各试验工况考虑了各个因素的不同水平值,以及土工织物单位面积质量分别与水头和细粒质量分数的交互作用(表1)。

表1 正交试验因素及水平

改进长筒模型试验分别选择了300 g/m2和500g/m2的土工无纺布对同一土样进行对比试验,主要研究土样各层土体颗粒及不同规格土工织物对渗透系数的影响。

2 “驼峰”现象及其影响因素分析

2.1 短筒试验k～t曲线上的“驼峰”现象

在试验过程中,内部土体未发生渗透变形,只是试样的渗透系数发生了一定幅度的变化。图3、图4描绘了18组典型试验工况所获得的短筒试样淤堵试验k～t曲线,其中图 3为相对低水头(水头差1m)的1～9工况的k～t曲线,图4为相对高水头(水头差2m)的10～18工况的k～t曲线。由这2幅图可见:①各工况组试验k～t曲线均具有“驼峰”特征,且“驼峰”现象持续时间都在200h以上,说明在整个淤堵过程中材料存在相当长一段时间的高渗透性阶段。②各工况的驼峰峰值点左侧曲线斜率比右侧曲线斜率大,说明在淤堵初期材料的渗透系数会较快增大。k随t变化的宏观趋势为先升后降,但在各时段内呈现阶段性凸凹起伏变化,这一点在1～9工况中更显突出,10～18工况的较高水头削弱了阶段性的凹凸变化。③各工况的“驼峰”峰值出现时间有差异,持续时间约为峰值前的1.3倍。峰值出现时间最长的84h和最短的53h分别发生在水头相对低的工况4和相对高的工况10。④各工况的“驼峰”峰值比渗透系数初始值及最终稳定值大,不同水头情况存在差异,1～9工况峰值约为初始值的5～10倍,是最终值的10～20倍;10～18工况峰值分别为初始值和最终值的10～20倍及 20～50倍,其中较大的峰值区在工况10～18下出现,说明高水头对峰值影响较大。⑤1～9工况的“驼峰”平均持续时间比工况10～18的长,说明低水头更易延长“驼峰”的出现时间及持续时间。

2.2 “驼峰”现象影响因素分析

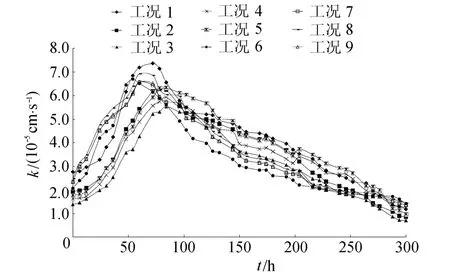
图3 淤堵试验 k～t曲线(工况1～9)

图4 淤堵试验 k～t曲线(工况10～18)

由图3和图4可见,各典型工况试验都出现了“驼峰”形k～t关系曲线,且各工况“驼峰”曲线的峰值kmax、峰值出现时间T1及峰值持续时间T2存在差异。下面将以此三要素作为考察指标,对试验结果进行综合分析。

2.2.1 单指标方差分析

按照正交试验方差分析方法,求得考察指标kmax,T1及T2的偏差平方和,进行F值检验,判断各因素的显著性,并通过显著性检验得到各因素的敏感性关系。

由单指标kmax方差分析结果可知,除细粒质量分数不显著外,其他因素都是显著或者高度显著因素,说明除细粒质量分数外,其他因素都或多或少地对峰值产生影响。F值确定显著性由大到小的排列顺序为:X1,X4,X2,X2×X3,X1×X2,X5,X3。

指标T1的方差分析结果表明,水头因素为高度显著因素,细粒质量分数及颗粒级配因素均为不显著因素,其他因素均为显著因素。各因素的 F值差异较大,高度显著因素的F值为显著因素的3倍多,说明在T1单指标考察中,水头影响占据绝对地位。F值确定由大到小的显著性排列为:X1,X5,X2×X3,X1×X2,X2,X4,X3。

各因素对T2指标的影响中,水头为高度显著因素,水头与土工织物单位面积质量的交互作用和干密度为显著因素,细粒质量分数、颗粒级配为不显著因素,F值确定由大到小的显著性排列为:X1,X5,X1×X2,X2×X3,X2,X4,X3。除一般显著因素外,最显著和不显著因素与T1指标的方差分析结果相近。

2.2.2 多指标方差分析

多指标分析的思路是“化多为单”,由于本试验的3个指标的影响权重不确定,宜采用回归评分法“化多为单”。首先进行经验打分,再利用 Excel的linest函数计算三元函数回归分析,得到回归系数及相应统计量,根据回归方程获得回归得分。

经计算,得回归方程为

根据此方程计算回归得分,即综合指标,对综合指标进行方差分析。由方差分析结果(表2)可知,水头与土工织物单位面积质量的交互作用对综合指标的影响最大,为高度显著因素;土样干密度、水头、细粒质量分数与土工织物单位面积质量的交互作用为显著因素;影响最小的是细粒质量分数和颗粒级配,为不显著因素。

表2 综合指标的方差分析结果

综上所述:①“峰值”现象反映的是渗透系数波动变化过程,渗透系数波动主要由颗粒移动导致的土样结构变化引起,这种结构变化会随着时间推移并在无新的外力作用下趋于平衡状态,使渗透系数波动较小直至稳定;②水头是单因素分析中影响最显著的因素,水头作为渗透水流的直接驱动力是导致土颗粒移动的主要因素;③土样干密度、颗粒级配等为颗粒移动提供了客观条件,但如果缺少外加荷载的作用,不论颗粒级配如何,不论干密度如何变化,颗粒也不会产生运动;④指标T1,T2受各个影响因素的影响几乎是一致的,说明峰值的出现时间越迟,峰值持续时间也越长。

3 “驼峰”现象产生的原因

3.1 长筒试验各层的“驼峰”现象

图5为300g/m2和500g/m2土工织物长筒试验土柱各段的k～t曲线。由图5可见,土样最上2层(Ⅶ层、Ⅷ层)的渗透系数最大,达到5.0×10-5cm/s左右,为整体渗透系数的2倍左右。土样中部Ⅳ层、Ⅴ层、Ⅵ层的渗透系数最小,与上部Ⅶ层、Ⅷ层的渗透系数相差近1个数量级。其他分段土层的渗透系数较接近,这在500g/m2的试验组中反映较明显。可见2组试验土样中都出现了3个渗透系数分层化区域。渗透系数变化的总体规律是两端最大、中间最小。

选择500g/m2土工织物试验组的数据,将3个分层化区域的渗透系数变化情况绘成曲线,见图6,可见,每个分层化区域的渗透系数也都存在“驼峰”现象,且以土样上下2端区域最明显。

图5 土样各土层 k～t曲线

图6 土层上、中、下各部分及整体k～t曲线

3.2 原因分析

通过上述对试验数据的分析,认为引起“驼峰”现象的主要原因是试样两端进出水口附近的土体受到水体流动引起的不平衡力及不平衡力矩较大,其中较细的土颗粒在渗透力拖曳下容易发生不规则移动,甚至随水流流出土体,从而改变了该区域土层的结构,使得渗透系数发生变化。而这种现象也在土样内部发生,只是这里的土样结构在两端土体的“制约”下受到的不平衡外力较小,引起的颗粒移动也较少,土层结构变化波动幅度相对较小。每一层土样或多或少地发生结构性改变,表现为渗透系数变化,最后集中表现为土样整体渗透系数的“驼峰”现象。可见,土工织物淤堵试验过程中形成的渗透系数与时间的“驼峰”现象来自土样细颗粒移动引起的土样和土工织物内部过水通道结构变化,且这种变化经过一定时间调整后会逐渐趋于稳定。

长筒试验相对短筒试验而言是一种“放大”,目的是探明究竟是哪一层土性质的变化引起了“驼峰”现象,两者试验结果是一致的。试验结果分析表明:对特定的试验土样,试验时为减小“驼峰”现象的影响,可以降低试验水头,在实际工程中,特别是新建初次使用的防渗工程,需要注意蓄水过程及防渗体的颗粒级配、干密度等。

4 结 语

土工织物淤堵试验过程中形成的渗透系数与时间的“驼峰”现象受到水头、土工织物单位面积质量、细粒质量分数、颗粒级配、干密度等因素的影响。其中,水头、颗粒级配及干密度影响最大。显然本文讨论的现象在实际工程中亦可能发生,特别是新建的反滤工程。从防止渗透变形和减少淤堵的角度看,应在设计和施工等环节考虑避免出现“驼峰”高峰值和缩短其出现期的措施。

:

[1]WU C S,HONG Y S,YAN Y W,et al.Soil-nonwoven geotextile filtration behavior under contact with drainage materials[J].Geotextiles and Geomembranes,2006(24):1-10.

[2]刘建华,郭忠印,丁志勇,等.公路土工合成材料淤堵试验方法研究[J].公路交通科技,2004(7):33-37.

[3]王钊,陆士强.土工织物滤层淤堵标准的探讨[J].水力发电学报,1991(3):55-63.

[4]FAURE Y H,BAUDOIN A,PIERSON P,et al.A contribution for predicting geotextile clogging during filtration of suspended solids[J].Geotextiles andGeomembranes,2006(24):11-20.

[5]方开泰.正交与均匀试验设计[M].北京:科学出版社,2001.

[6]陶同康.土工合成材料与堤坝渗流控制[M].北京:水利水电出版社,1999.

[7]佘巍,陈轮,王钊.土工织物梯度比试验研究的新进展[J].长江科学院院报,2006(2):58-60.

[8]ENNION M P,ALINE F N R,MARIA L G R,et al.A study on biological clogging of nonwoven geotextiles under leachate flow[J].Geotextiles and Geomembranes,2008(26):205-219.

[9]陈星柏.关于土工织物反滤层的渗透准则[J].水利学报,1990,21(9):47-51.

[10]GB50290—1998 土工合成材料应用技术规范[S].

[11]孔丽丽,陈守义.武山尾矿坝无纺土工织物滤层化学淤堵问题初探[J].岩土工程学报,1999,21(4):444-449.

[12]FISCHER G R,MARE A D,HOLTZ R D.Influence of procedural variables onthe gradient ratio test[J].Geotechnical Testing Journal,1999(22):22-31.