应用混沌理论对煤矿瓦斯浓度预测*

刘荷花

（太原大学，山西太原 030009）

0 引言

煤矿井下瓦斯直接关系到煤矿调度、生产计划及矿工的生命安全，对瓦斯浓度进行有效的预测、预报，一直是安全信息处理所面临的重要课题。煤矿瓦斯浓度具有不确定性，受自然因素（如地质构造、煤层厚度、煤体结构、埋藏深度等）和开采技术等多种因素影响，具有非线性特性。

混沌现象是自然界广泛存在的一种不规则运动，是一种非线性的复杂行为。混沌系统，是一种可以从无序和复杂中产生出有序和规律的系统，具有对初始条件的极端敏感性，即所谓的“蝴蝶效应”。［1］混沌理论，是对存在于非线性系统中无序的研究。为解决非线性问题提供了一种很好的理论工具。

1 基本原理及国际研究现状

煤矿瓦斯浓度数据通常是一个时间间隔为Δt的单变量的时间序列（x1，x2，…，xi），传统的预测方法是直接从这个序列形式分析它的时间演变，但由于时间序列是许多因子相互作用的综合反映，其中蕴藏着参与整个系统运动的全部变量的痕迹，因而必须将这一时间序列扩展到三维甚至更高维的相空间中去，才能把时间序列中的信息充分地显露出来。

Takens理论运用基本的相空间重构方法，在满足某些条件下，保证从一个吸引子到重构空间的映射是一个嵌入，通过一对一的映射，保证映射的微分结构不变，实现相空间中轨道的重构［2］，使得沿时间轴排列的一维时间序列可以通过重构相空间的方式恢复原系统的特征。

D.Kugiumtzis提出了相空间重构的嵌入窗法，指出时延t的选取不应独立于嵌入维数m，而应依赖于嵌入窗 τw=（m-1）t，并且要求 τw≥τp，这里 τp为混沌系统的平均轨道周期。严格来讲混沌系统不存在周期性，然而对于存在伪周期的低维混沌系统来讲，平均轨道周期是指混沌吸引子在永不重合而又彼此相似的相空间轨道上振荡的平均周期［3］。

1999年，H.S.Kim等人基于嵌入窗法的思想提出了C-C方法，该方法使用关联积分同时估计出时延与嵌入窗。然后陆振波等人提出改进的相空间重构参数选择方法。

本文提出一种基于C-C方法，确定最优时延与嵌入窗的新方法，该方法对最优时延的选择更准确，对最优嵌入窗误判的可能性大大降低。

2 改进计算相空间参数算法和混沌吸引子判定

采用一种基于关联积分的统计:对时间序列x={xi|i

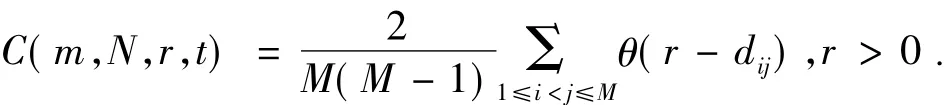
其中dij= ‖Xi-Xj‖（∞），θ（x）=0，若x＜0;θ（x）=1，若x＞ =0。

关联积分是个累积分布函数，表示相空间中任意两点之间距离小于r的概率。这里点与点之间的距离用矢量之间的距离表示［4］。定义此关联积分的检验统计量:

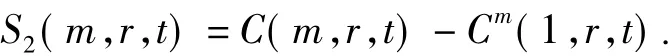
用来描述非线性时间序列的相关性，并由统计量S2（m，N，r，t）来寻找延迟时间 τ。

改进的计算过程不必将以上时间序列平均分为t个子序列，而直接以一个序列进行相空间重构。

选择几个代表值rj，并定义差量:

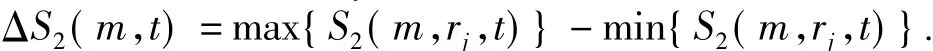
ΔS2（m，t）度量了S2（m，r，t）～t对所有半径r的最大偏差，局部最优时间t则对应于ΔS2（m，t）的最小值。对所有的m，ΔS2（m，t）的最小值几乎相同。于是时滞参数τ就选为第一次出现这些最优的时间。由于C-C方法中S2（m，t）的第一个零点并不总是等于ΔS2（m，t）的第一个极小值点，于是，对于最优时延τd，不考虑S2（m，t）的第一个零点，只取ΔS2（m，t）～t的第一个局部极小点作为计算该参数的唯一标准。

根据BDS统计结论可以得到N和m，r的合理估计，这里取N=600，m=2，3，4，5，ri=i*0.5，σ =std（x）（σ 为时间序列的标准差），i=1，2，3，4。计算=1，2，…，N}，以时延t，嵌入维数m，重构相空间X={Xi}，Xi为相空间中的点，则嵌入时间序列的关联积分为:

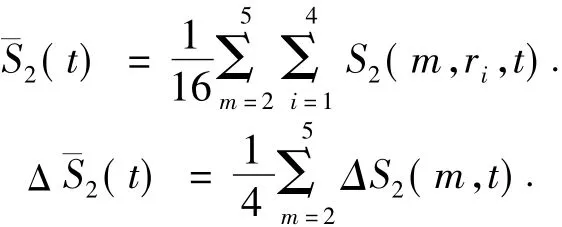
寻找ΔS2（t）的第一个局部极小点即为最优时延τd。另外，定义指标:

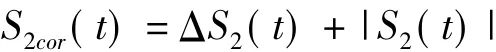
寻找S2cor（t）的全局最小点即可获得嵌入窗 τw，即平均轨道周期的最优估计。由 τw=（m-1）t，得出m=τw/t+1。

研究非线性系统单一变量时间序列的目的之一是判定系统中是否存在混沌吸引子。

混沌性的鉴别主要是指在某一置信度下判断识别，其方法有很多，现在使用最为广泛的是Lyapunov指数法。

Lyapunov指数是刻画混沌吸引子的最主要的参量。混沌运动的基本特点是对初始条件敏感，两个极靠近的初值所产生的轨道，随时间推移按指数方式分离，Lyapunov指数就是刻画这一现象的量。

3 建立加权一阶局域近似模型

嵌入维数m和时间延迟t选好后，就可以对一混沌时间序列进行预测，在目前混沌时间序列的预测方法中［5］，一阶局域法效果最好。

本文选用加权一阶局域法来对瓦斯浓度进行预测。

在该方法中把相空间轨迹的最后一相点作为中心点，把离中心点最近的若干轨迹点作为相关点，计算出各点到中心相点Xk之间的欧氏距离，找出Xk的局域参考向量集，Xki（i=1，2，…，q），并且点Xki到Xk的距离为di，设di是dm中的最小值，定义点Xki的权值为:

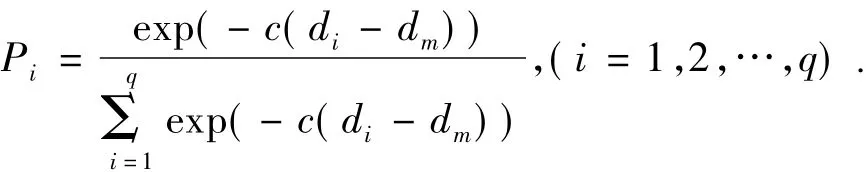
式中c为系数，一般取c=1.则一阶局域线性拟合为Xki+1=ae+bXki，（i=1，2，…，q），e=（1，1，…，1）T。式中:a，b为待定系数，当嵌入维数m=1时（m＞1的情况类似），为了使平方误差达到最小，使预测模型与试验数据达到最佳的拟合，应用加权最小二乘法有:

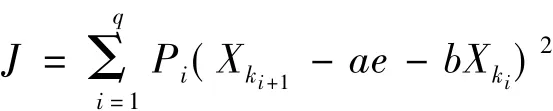
则J为待定系数a，b的函数，两边分别对a，b求偏导并令其为零，整理得到:

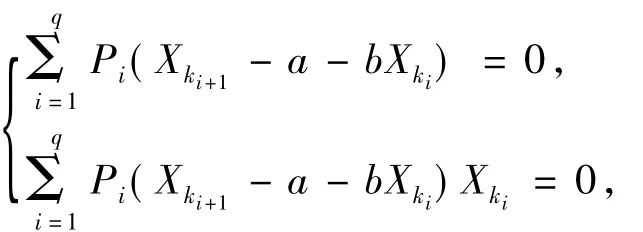
化简上式得到关于系数a，b的方程组为:qq

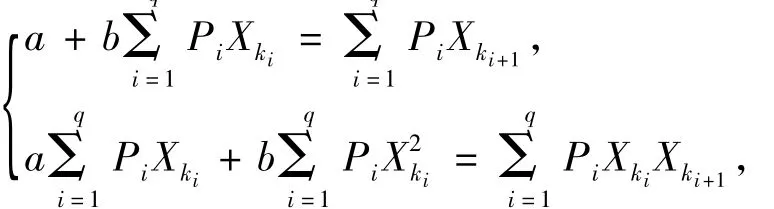
解上述方程组则可得到a，b，然后代入式Xki+1=ae+bXki，得预测公式。

根据预测公式进行预测，显然参数向量集为Xki（i=1，2，…，q）的一步预测为Xki+1（i=1，2，…，q）。

这种预测方法使用的关系式Xki+1=ae+bXki，（i=1，2，…，q），阶数为1所以称为一阶近似预测。

瓦斯浓度受许多因素相互影响，具有复杂的演化规律，表现出混沌特性是可能的。在实际的瓦斯浓度的测量数据中，噪声与混沌往往并存，既有确定性成分，也有随机性成分。首先根据改进的C-C方法分别重构相空间X（ti）=［x（ti），x（ti+ τ），x（ti+2τ），…，x（ti+（m-1）τ）］（i=1，2，…，N），按照上述算法分别计算出相空间重构的两重要参数，即最优时间延迟τ与最佳嵌入维数m。其次要对其进行混沌性的鉴别，计算出试验序列的最大Lyapunov指数［6］，在煤矿瓦斯浓度的重构相空间中，建立加权一阶局域近似模型来预测所选那组数据的下一刻的瓦斯浓度值，将预测结果与实际值相比较，分析误差。

为衡量不同因素对预测结果的影响情况，用预测值与实际值的均方差作为评判预测效果的一个指标

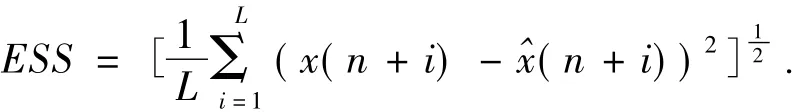
式中:x（n+i）表示实际值，（n+i）表示预测值。ESS小，说明预测值偏离实际值的程度小，预测效果较好;ESS大，说明预测值偏离实际值的程度大，预测效果就差［7］。

4 结论

本文针对煤矿瓦斯浓度的非线性特性，在C-C算法的基础上作了一些改进，来确定煤矿瓦斯浓度混沌时间序列分析的时间延迟和维数，采用加权一阶局域法实现了煤矿瓦斯浓度的短期预测，有效反映了煤矿瓦斯浓度发展趋势，为煤矿提前采取安全措施提供科学依据。

［1］CHENG Jian，QIAN Jiawsheng，GUO Yi-nan.Least Squares Support Vector Machine for Gas Concentration Forecasting in Coal Mine［J］.International Journal of Computer Science and Network Security，2008，6（6）:125-129.

［2］张剑英，程健，侯玉华，等.煤矿瓦斯浓度预测的ANFIS方法研究［J］.中国矿业大学学报，2009，36（4）:494-498.

［3］BARANA G，TSUDA I.A New Method for Computing Lyapunov Exponents［J］.Physica Letter A，2006，175:421-427.

［4］WOLF A，SWIFT J B，SWlNNEY H I，VASTANO J A.Determining Lyapunov Exponents From a Ttime Series［J］.Physica，2005，16D:285-317.

［5］TAKENS F.Determining Strange Attractors in Turbulence［J］.Lecture Notes in Mathematics，2006，898:366-381.

［6］王海燕，盛昭瀚.混沌时间序列相空间重构参数的选取方法［J］.东南大学学报（自然科学版），2008，30（5）:113-117.

［7］王妍，徐伟，曲继圣.基于时间序列的相空间重构算法及验证（一）［J］.山东大学学报（工学版），2009，35（4）:109-114.