Duffing混沌系统的全局快速Terminal滑模变结构控制
2011-09-06赵黎明
赵黎明
(广东海洋大学信息学院,广东湛江524003)
混沌系统是一类普遍存在且重要的非线性系统,具有复杂和难以预测等行为,而Duffing方程系统,不仅是描述共振现象、调和振动的简单数学模型,而且是一个典型的非线性振动系统,极具代表性,许多工程实际问题都可转化为该类方程系统来研究。同时,在一定条件下存在奇异吸引子,并产生混沌现象[1]。因此,研究Duffing方程混沌系统的稳定控制问题具有重要的理论与实际意义。
针对Duffing方程混沌系统,已提出许多不同的控制方法[2-8],其中:文献[2]研究了基于 Lyapunov方法的稳定控制问题;文献[3]研究了基于状态观测器的混沌控制方法;文献[4-5]研究了外加激励的混沌控制方法;文献[6]研究了状态反馈混沌控制方法;文献[7-8]研究了自适应混沌控制方法。由于Duffing方程混沌系统中存在不确定性,因此研究不确定Duffing方程混沌系统的稳定控制问题必将具有重要的实际意义。而由于滑模变结构控制方法是一种重要的鲁棒控制方法,因此本文重点研究Duffing方程混沌系统的Terminal滑模变结构控制,并设计一种全局快速Terminal滑模面。
1 Duffing方程混沌系统描述及研究内容
考虑Duffing方程混沌系统[2]
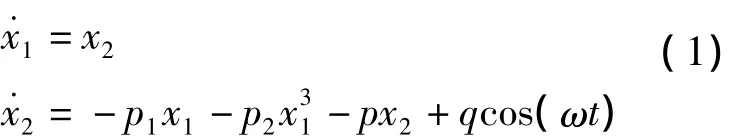
其中,x=(x1,x2)T为系统状态,p1、p2、p、q、w 为系统的不确定参数且在一定范围内变化。
当 p1= -1、p2=1、p=0.25、q=0.27、w=1,x1=1、x2=1时,系统出现混沌现象,其对应混沌吸引子的相轨迹如图1所示。
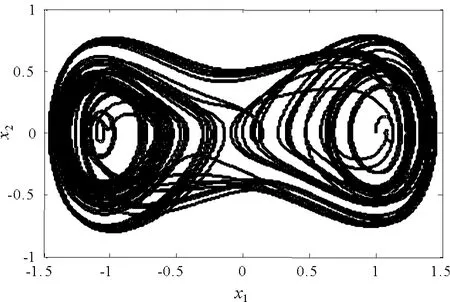
图1 Duffing系统混沌吸引子的相轨迹
研究混沌系统(1)的渐近稳定控制问题,即设计控制律,使系统(1)状态x渐近收敛至x=0,其受控系统为

其中f(x)= -p1x1-p2x31-px2+qcos(ωt)为系统的不确定性。根据混沌系统有界性可知,f(x)满足有界性条件。
由于系统(1)存在不确定性,而滑模变结构控制具有很强的鲁棒性,因此本文研究其滑模变结构控制问题。在传统的滑模变结构控制中,通常通过构造一个线性的滑模面,在控制律作用下使系统到达滑模面后,系统状态沿期望的滑动模态渐进地收敛到零点。为了改善系统状态的渐进特性,一些学者研究了 Terminal滑模变结构控制[9-11],通过设计非线性滑模面,使得当系统到达滑模面后,系统状态能在有限时间范围内到达闭环零点。
2 基于全局快速Terminal滑模变结构控制器设计
针对系统(1),根据全局快速Terminal滑模变结构控制原理[12],设计了一种新的全局快速Terminal滑模面,其形式为

其中,α,β >0,0< σ <1。正是由于非线性项 β·sign(x1)|x1|σ的存在,改善了系统状态沿滑模面趋向于平衡点的速度,并使其在有限时间范围内收敛至x=0。
由于系统不确定性f(x)的存在,因而为其设计鲁棒控制律,根据文献[12]可得,控制律u为
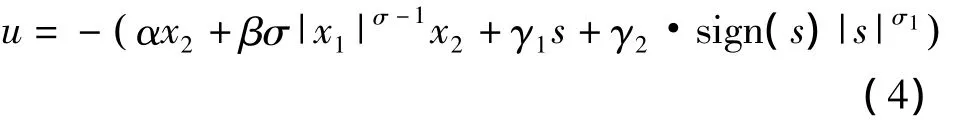
其中,γ1,γ2>0,0 < σ1<1。同时,为了满足闭环系统稳定条件γ2应满足

并选择 γ2为

其中,δ>0,L为|f(x)|的上界。
3 稳定性分析
Duffing方程混沌系统(1)在控制律(4)作用下,其受控系统如式(2)所示。针对受控系统(2),定义Lyapunov函数V为

对其求导,可得


由于 γ2-f(x)/(sign(s)|s|σ1)>0,可知式(9)满足

可见,在控制律(4)作用下,受控闭环系统(2)满足Lyapunov稳定性条件。
4 仿真实验
令Duffing方程混沌系统(1)状态的初始值为x1=1、x2=0,系统参数选取为 p1= -1、p2=1、p=0.25、q=0.27、w=1,控制律(4)参数选取为 α =2、β =1、σ =0.75、γ1=90,γ2=L/|s|0.4+ δ、δ=1.2、σ1=0.4进行仿真,仿真结果如图2所示。

图2 闭环系统仿真效果图
由仿真结果可以看出,采用本文提出的控制方法,不仅能够很好地抑制Duffing方程混沌系统(1)混沌现象的产生,而且使得受控Duffing方程混沌系统(1)实现了稳定控制。
5 结论
本文研究了Duffing方程混沌系统基于全局快速Terminal滑模的有限时间稳定控制问题。通过设计一种新的全局快速Terminal滑模面,使得当系统到达滑模面后,系统状态能在有限时间范围内到达闭环零点。由仿真结果可以看出,采用本文提出的控制方法,对于具有典型非线性振动特性的Duffing方程混沌系统具有很强的鲁棒性,不仅能够很好地抑制其混沌现象的产生,而且使得受控系统实现了有限时间稳定控制。
[1]陈关荣,吕金虎.Lorenz系统族的动力学分析、控制与同步[M].北京:科学出版社,2003:1-4.
[2]徐红兵,吕炳朝.基于Duffing方程不确定性模型的混沌控制[J].系统工程与电子技术,2000,22(2):15-17.
[3]刘剑,宋珊珊,刘美菊,等.一种基于状态观测器的Duffing系统的混沌控制[J].沈阳建筑大学学报(自然科学版),2009,25(2):395-398.
[4]沈建和,陈树辉.混沌Mathieu-Duffing振子的开闭环控制[J].应用数学和力学,2009,30(1):21-29.
[5]褚衍东,李险峰,张建刚.Van der Pol-Duffing耦合系统的分岔与混沌控制[J].江南大学学报(自然科学版),2007,6(1):119-123.
[6]周群利,张绍德.基于反馈线性化的Duffing混沌系统控制[J].安徽工业大学学报(自然科学版),2007,24(1):58-62.
[7]王中生,李伟锋,廖晓昕.不确定Duffing混沌系统的自适应跟踪控制[J].华中科技大学学报(自然科学版),2005,33(2):64-66.
[8]周培培,曹鸿钧.Helmholtz-Duffing振子同宿分岔的自适应反馈控制[J].科学技术与工程,2008,8(7):1769-1773.
[9]Yuqiang Wu,Xinghuo Yu,Zhihong Man.Terminal sliding mode control design for uncertain dynamic systems[J].Systems &Control Letters,1998,34(5):281 -287.
[10]Yong Feng,Xinghuo Yu,Zhihong Man.Non - singular terminal sliding mode control of rigid manipulators[J].Automatic,2002,38(12):2159-2167.
[11]Xinghuo Yu,Man Zhihong.Fast terminal sliding-mode control design for nonlinear dynamical systems[J].IEEE Transactions on Circuits and Systems,2002,49(2):261 -164.
[12]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:320-360.
