移动机器人动态目标规划研究

2011-09-06胡玉兰

沈阳理工大学学报 2011年3期

山丹，胡玉兰

(沈阳理工大学信息科学与工程学院，辽宁沈阳110159)

人工势场法(potential field)［1］是 Khatib 于1956年提出的，其基本思想是构造目标位姿引力场和障碍物周围斥力场共同作用的人工势场，搜索势函数的下降方向来寻找无碰撞路径。人工势场法以其描述简单、计算效率高、对于传感器要求低(只需要声纳就可实现)，得到了广泛的研究和应用，特别适合于机器人在未知动态环境中的避碰运动规划。但是由于人工势场法依据的是局部环境信息，缺乏宏观的自我调控能力，从而容易产生局部极小的问题。当机器人处于局部极小值时，停止不前或来回摆动。局部极小点问题的存在，极大的限制了人工势场法的推广运用。本文对引力函数和斥力函数做改进避免了人工势场法的这一局限性。

1 改进的人工势场法

1.1 改进的斥力场函数

通过对斥力场函数进行优化，让机器人在接近目标点时，不仅引力场的引力不断减小，同时斥力场的斥力也在不断减小，这样就解决了机器人目标不可到达问题［2］。其斥力场函数表达式为

其中:ε为斥力场的正比例系数;ρ(q，qobs)为机器人的当前位置q到障碍物的表面位置qobs的距离;ρ(q，qgoal)为机器人的当前位置q到目标点位置qgoal之间的距离;ρ0为障碍物所能影响的范围;n为常数。

根据公式(1)，当机器人离目标点越来越近时，虽然目标点对机器人产生的引力越来越小，但是障碍物对机器人产生的斥力也越来越小，当机器人到达目标点时，机器人的引力和斥力均为零。

当机器人不在目标点时，即q≠qgoal，斥力可以表示为

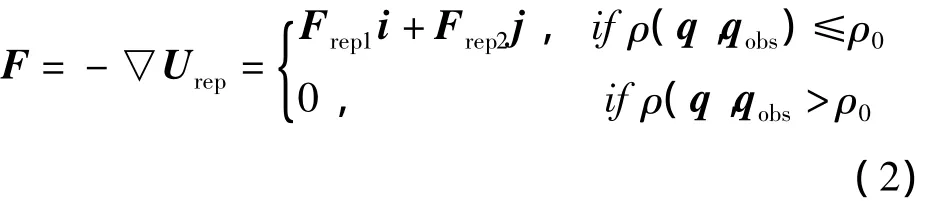
其中，

i=▽ρ(q，qobs)和 j= －▽ρ(q，qgoal)是两个单位向量，一个向量是由障碍物指向机器人，另一个矢量由机器人指向目标点。该受力分析如图1所示。可以看出斥力分量Frep1i让机器人远离障碍物，分量Frep2j吸引着机器人向目标前进。

由公式(1)可知，当n=0时改进的斥力场函数变为传统的人工势场函数，因此n不能取0，本文选择n＞0。下面通过分析n的取值来说明新的斥力场函数能够保障机器人顺利避开障碍物，最终到达目标点。

图1 机器人在改进的斥立场函数作用下的受力分析

(1)当0＜n＜1时

公式(1)在目标点q=qgoal时，函数不可微，由公式(3)、(4)可知，当 ρ(q，qobs)＜ ρ0且 ρ(q，qgoal)≠0时，即机器人在障碍物的影响范围之内，但不在目标点。当机器人接近目标点时［3］，ρ(q，qgoal)逐渐接近于零，从上面两个公式可以看出，斥力函数第一个分量Frep1趋近于零，而第二个分量Frep2趋近于无穷大，这个分量是吸引机器人向目标点运动，所以这时机器人相当于，只受目标点对它的吸引力，机器人能到达目标点。

(2)当n=1时

同样 ρ(q，qobs)＜ ρ0且 ρ(q，qgoal)≠0，斥力两分量为

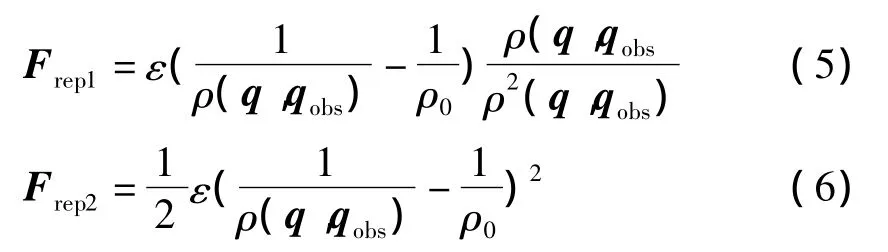
当机器人接近目标点时，ρ(q，qgoal)逐渐为零，因此斥力第一个分量Frep1逐渐趋近于零，而第二个分量Frep2趋近于一个常量，第二个分量吸引着机器人向目标点运动。所以当n=1时保证了机器人向目标点运动。

(3)当n＞1时

斥力场函数在目标点是可微的，随着机器人接近目标点，总的斥力趋近于零，只剩下目标点对机器人的引力，同样确保了机器人不断地向目标点运动并且最终能够到达目标点。

综上所述，改进的斥力场函数能够很好地解决障碍物在目标点附近的局部最小值问题。

他是一个不知道自己有什么弱点的人，比如他说话时结巴，可他自己不知道，或者说他从来没有承认过这一点，他的妻子萍萍是一个漂亮的女人，留着很长的头发，不过大多数时间她都是把头发盘起来，她知道自己的脖子很长很不错，她有时候穿上竖领的衣服，她的脖子被遮住了大半以后，反而更加美妙了，那衣服的竖领就像是花瓣一样。

1.2 基于动态目标的改进引力场函数

传统的人工势场法只适合于目标是静态环境［4］，如果目标是动态的，传统的人工势场函数并不适合。所以本文提出一种基于目标是动态运动的改进的引力场函数。为简化分析，做以下假设:

假设1机器人为一质点，其位置q和速率v都是已知的;

假设2目标机器人的位置qtar和速率vtar都是已知的，且|vtar|＜ |vmax|。

通常，引力场被定义为一个只与机器人和目标距离相关的函数，而且目标被定义为空间中一个固定的质点。但当目标在不断移动时，传统的势场函数就不能使用了，需要定义一个改进的引力场函数来适应这种情况。

改进的引力场函数为

其中:q(t)和qtar(t)分别对应t时刻围捕机器人和移动目标机器人的位置;v(t)和vtar(t)分别是t时刻围捕机器人和移动目标机器人的速度矢量;║qtar(t)－q(t)║是t时刻围捕机器人与移动目标机器人的欧几里德距离;║vtar(t)－v(t)║是t时刻围捕机器人与移动目标机器人速度的相对值;аq和аv是正比例系数;m和n是两个正的常量。

从上式容易看出如果аv=0，m=2，那么新引力场函数就会退化为传统引力场的二次函数形式

公式(8)不包括机器人与目标机器人相对速度的信息。相应地，传统引力场函数的引力只被定义为相对位置的负梯度方向，同样与机器人和目标机器人的相对速度无关。

新引力场函数Uatt(q，v)是一个关于位置q和速度v的函数。因此，定义相应的引力应该定义为关于位置和速度的负梯度方向

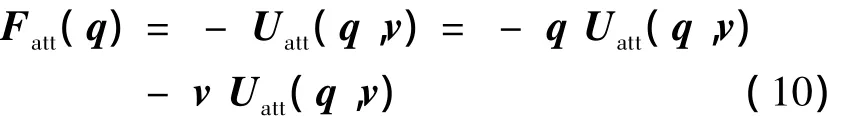
式(7)中m和n的值对新引力场函数有很大影响，不同取值对引力场函数有着不同影响，因此必须选择合理的m和n的值，下面将讨论m和n的参数选取情况。

可以看出，当0＜m＜1，在q=qtar时引力场函数 Uatt(q，v)不可微;当 0 ＜ n≤1，v=vtar时引力场函数Uatt(q，v)不可微。在对移动目标进行构建引力场函数时，可以将应用情况大致分为两类，一类可以称为“软围捕”，另一类称为“硬围捕”。“软围捕”，即机器人以零相对速度接触到移动目标之后以与目标相同的速率进行运动。“硬围捕”，即机器人只考虑怎样到达移动目标(q=qtar)而不考虑相对速度。

当 q≠qtar，v≠vtar时，将式(7)带入式(10)，可得

其中，

其中，nRT是从机器人到目标机器人的单位矢量，nVRT是围捕机器人相对于目标机器人的相对速度的单位矢量。引力场函数的引力以及机器人目标的位置和速度关系如图2所示。引力Fatt由两个分量组成［5］:第一个分量Fatt1(q)将机器人向目标吸引，缩短目标和机器人的距离;第二个分量Fatt2(v)拉扯着机器人以相同速率运动。

图2 在二维空间中的改进引力场引力

从公式(12)和(13)可以看出，当机器人接近目标时，也就是║qtar(t)－q(t)║接近于零，即Fatt1(q)接近于零;当机器人接近目标点时，即Fatt2(v)接近与零。因此，当机器人的位置和速度都接近与目标时，虚拟引力Fatt也接近于零。当围捕机器人捕获到目标，然后以相同速率运动时，引力场引力为零，因此围捕机器人可以与机器人一起运动。对于“软围捕”问题，对m和n的选择是必不可少的。而对于“硬围捕”则没有这样的约束，只要m和n都大于零就行。

2 改进人工势场法仿真实验

为验证改进式人工势场法的有效性，本文在VisualC++6.0和Matlab7.1这两种工具联合开发的仿真平台上进行仿真实验。仿真结果如图3～6所示。

图3 围捕机器人穿越障碍物

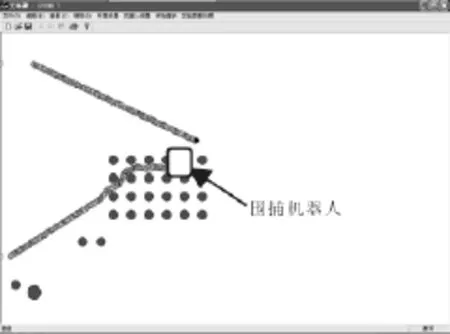
图4 侦测到入侵机器人

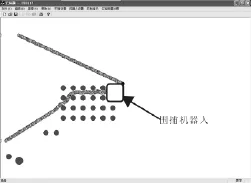
图5 对入侵机器人进行围捕图

图6 围捕机器人成功围捕入侵机器人

在静态复杂环境下，通过给定围捕机器人的起始点以及动态目标起始点和运动轨迹，验证算法的可行性。机器人圆形的全方位移动机器人，机器人的侦查周期大于其运动周期，机器人仅依靠自身的传感器进行环境探测，探测范围是机器人自身半径的5倍。机器人在探测范围外时，避障运动见图3。进入探测范围时，机器人发现目标，并靠拢且跟踪动态目标点见图4、图5。图6为入侵机器人停止运动，表明围捕机器人成功围捕入侵机器人。