基于VaR约束的最优投资组合选择

尉轶昊，毛 宏

（上海第二工业大学经济管理学院，上海 201209）

基于VaR约束的最优投资组合选择

尉轶昊，毛 宏

（上海第二工业大学经济管理学院，上海 201209）

通过建立期望效用-VaR模型，借助于Matlab和Monte Carlo 模拟技术，深入探讨和分析了以VaR作为风险测度标准及约束时，拥有不同风险偏好及初始财富值的投资者在进行投资决策时对最优投资组合的理性选择，以中国A股、公司债券和国债这三大证券在2004 ～ 2006年及2009 ～ 2010年间5年的历史数据为估计模型的参数值，并讨论了在中国资本市场中运用投资组合理论分散风险、稳定收益的可行性。

VaR；资产组合；效用函数；风险偏好；财富值；MATLAB

0 引言

投资组合，或称投资组合管理（Portfolio Management）是指投资者把投资的资金有计划地分配于多种资产类型中（如股票、债券、不动产和实业投资等），使各类资产的配置达到最佳组合，从而分散风险、稳定收益，即寻求风险一定时的最大收益或收益一定时的最小风险。虽然投资组合理论可以应用于所有风险资本的投资活动，但由于证券具有交易公开、数据易得等特点，同时又是各种风险资产的代表，因此该理论长期以来都着重应用于对证券组合的分析，因而又被称为证券组合理论（Securities Portfolio Management），即对投资进行计划、分析、调整和控制，从而将投资资金分配给若干不同的证券资产，如股票、债券及证券衍生产品，形成合理的资产组合，以期实现资产收益最大化或风险最小化的经济行为。证券投资组合是一个不确定市场的稳定工具，在21世纪的今天，随着我国资本市场的不断发展和深化改革，中国的证券市场也在逐渐向半强乃至强有效的市场靠拢。在这样的转变过程之中，逐渐尝试以组合理论作为投资决策的依据无疑是据有前瞻性和深远意义的。

1 模型及理论概述

1.1 现代投资组合理论概述[1]

有关投资组合的理论始于20世纪30年代。Hicks在其《关于简化货币理论的建议》一文指出：“要计算从事多项投资的总风险，不能简单地将各独立投资所承担的风险相加，由于大数定律的存在，分散投资的总风险小于将全部资金投资于同一资产的风险，当风散化程度很高时，理论上总风险将降为最小。”Hicks的论述表明了运用投资组合可以有效地降低风险，但他没有深入地解释为何要进行组合投资、如何进行组合投资以及如何判别组合投资的效用等问题，因此不能算作是一个完整的体系。

Markowitz是第一个将不确定因素引入资本理论模型的人。1952年Roy提出的“安全第一（safety first）”模型与马克维茨理论的框架相似，但由于Markowitz的研究成果先于Roy发表，因此人们通常认为马克维茨是现代投资组合理论之父。Markowitz的均值-方差模型将方差作为风险的测度标准，在定量上证明了投资组合可以起到降低风险的作用。

1958年，Tobin将无风险资产引入Markowitz的模型，使得投资组合理论取得了重大的突破。Tobin认为正确的投资策略应该是将资产在无风险资产（现金或国债等）与风险资产（公司债券或股票等）之间进行分配。这是因为投资者投资风险资产虽然将获得更高的收益，但同时也要承担更高的风险，而投资于无风险资产则正好相反。由于收益产生的正效用边际递减而风险导致的负效用边际递增，因此，只有当最后一单位无风险资产所产生的边际正效用与最后一单位风险资产所产生的边际负效用之和为零时，投资者的总效用才能被最大化。换言之，理性投资者对投资组合的选择应遵循的条件是：边际收益等于边际风险。由此得出的结论是：在确定投资组合时，首先应当在风险资产和无风险资产之间做出分散投资的决策，其次再根据Markowitz的理论确定出投资于不同风险资产的比例。此即Tobin的第一分离定理（Separation Theorem）。分离定理的经济学含义在于，持有无风险资产的比例反映了投资者的风险偏好，而最优投资组合与投资者的风险偏好是相互独立的。

虽然Tobin完成了资产选择的工作，但他并未脱离Markowitz的全方差模型，而在当时的技术条件下，其巨大的计算量成了最主要的限制条件。1963年，William Sharpe又提出了新的见解和模型，即单指数模型。Sharpe认为证券价格与市场的升降是协同运动；证券之间的收益相关性主要是由于各种证券对市场共同反应造成的；证券收益与市场指数的收益之间存在线性函数关系。按照这一模型求解最优投资组合时，每种证券只需估计期望值、方差、与市场指数的协方差三个参数，使得Markowitz和Tobin模型的复杂度大大降低，理论的应用成本达到了可运用到实际投资活动中的水平。

1966年，King首先运用单指数模型对1927～1960年纽约证券交易所不同行业的63种股票的风险性质进行了实证研究。实证得出的结论是：股票价格的确随市场的波动而协同变化，但变化的程度却因行业的不同而有所不同，即行业因素也有助于股票价格变动的预测。在此基础上，Marshall Blume等人提出了多因素模型。多因素模型除了市场因素外，也将其它非市场因素（如通货膨胀率、失业率、行业等因素）的变动纳入到对投资组合的考量中。至于单指数模型和多因素模型之间的优劣比较，至今尚无定论。

现代投资组合理论不断向实用化发展的同时，理论本身也在不断地发展和完善。Markowitz的理论着重对风险资产投资的研究，指出投资者应当沿着有效前沿进行最优投资组合的选择。但如果允许将无风险资产和风险资产进行组合，那么有效前沿将发生怎样的变化？若投资者的投资行为与该理论一致，当资本市场达到均衡时资产收益将如何确定？风险的测度标准是什么以及期望收益与风险之间的函数关系怎样？这都需要做进一步的探讨。

William Sharpe，John Lintner和Jan Mossin从实证研究的角度出发，进一步探讨了这些问题，共同提出了资本资产定价模型（CAPM）。但由于该模型中的一些假设与现实中的情况存在很大差距，放松某些假设条件的非标准资本资产定价模型由此诞生，包括风险资产可容许有效投资组合模型、存在无风险资产的可容许有效投资组合的模型、上下模糊可能性投资组合模型、具有风险价值约束的投资组合模型等。本文研究的内容就是一种以VaR作为风险价值约束的投资组合模型。

1.2 VaR模型概述

VaR英文为Value-at-risk，通常称为风险价值，其含义为“处于风险中的价值”。它是指在市场正常波动下，某一金融资产或证券组合的最大可能损失。更为精确地讲，就是在一定的持有期内和给定置信度下，某一金融资产或证券组合可能遭受的最大损失，用数学表达式可表达为[2]：

其中：β为置信度；(,)Lwr为证券组合在持有期内的损失；VaRβ为金融资产或证券组合在置信度β下处于风险中的价值。

在实际应用中，考虑一个证券组合，假定0w为初始投资额；w为期望值；*w为金融资产或证券组合的最低价值；r为其在持有期内的收益率；µ是r的均值；σ为r的的波动率；*r是r在给定置信度下的最低收益率。可以将VaR定义为相对于期望值的损失，即

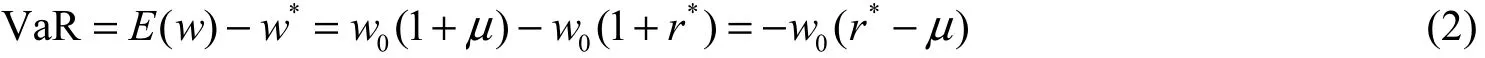
其中：0w为组合的初始投资额；wσ为组合收益的标准差（波动率）；t∆为持有期；Zβ为根据新巴赛尔协议的规定，当给定置信度为99 %时的标准正态分布Z值。

1.3 均值-方差模型、均值-VaR模型与效用-VaR模型的比较

Markowitz均值-方差模型试图确定在投资者效用最大化情况下资产组合的构成。效用最大化的标准是在风险一定的情况下实现收益的最大化，在收益一定的情况下实现风险的最小化，如图1所示：

图1 均值-方差模型中组合的有效前沿Fig.1 The efficient frontier of mean-variance model

纵轴表示期望收益W，横轴表示风险的测度标准——标准差σ，AB称为投资的有效性前沿，这是因为在该曲线上满足同风险下收益最大和同收益下风险最小这一标准[3]。

Markowitz投资组合理论的问世被称为第一次“华尔街革命”。尽管这一理论系统地构造了一套投资组合的选择方法，并为实际投资家广泛使用，但是它在理论上仍然存在不少缺陷。相比于均值-VaR模型，后者计算的是在某个置信度下投资人可能的最大损失，而方差仅仅反映了收益的波动大小[4]。

在均值-VaR模型中，不同置信度下可以画出不同的有效前沿，如图2所示：

图2 均值-VaR模型中组合的有效前沿Fig.2 The efficient frontier of mean -VaR model

置信度越高，有效前沿图像越往右移，在相同期望收益水平之下得到最优配置所对应的风险（即此时可能遭受的最大损失）也就越大；相反，置信度越低，有效前沿图像越往左移，在相同期望收益水平之下得到的最优点的风险也就越小[5-6]。本文根据新巴塞尔协议的规定，将选择99 % 作为置信度加以论述。

均值-VaR模型考虑的是，在可能遭受最大损失一定的情况下使期望收益最大化的投资组合方式：在满足风险要求的条件下，其用以衡量投资成果的指标局限于收益率。而本文采用的期望效用-VaR模型，在均值-VaR模型的基础上更进一步，运用效用函数假定投资者的财富为一随机过程，并引入风险厌恶系数作为对投资者风险态度的度量：既考虑了组合的收益情况，又考虑了具有不同风险偏好的投资者在VaR约束下的最优投资组合情况，最后还分析了初始投资取不同值时对最优投资组合的影响。

1.4 效用理论概述

所谓效用（utility）是指金钱、物品、劳务等给人提供的满意度，常被用于衡量人们对某些事物的主观态度、偏好、倾向等。在投资组合的决策过程中，通过效用指标可以将某些难以量化、有质地差别的事物加以量化，通常而言，就是以效用来衡量对待风险的态度，并以效用函数表示，其基本形式为U=U(w)，其中w表示某项决策可能的结果值。依据决策者的主观愿望和价值取向的不同，结果值对决策者的价值和作用也不同，而反应结果值对决策者价值大小的值称为效用以U表示。

由于效用函数视决策者对风险态度的不同而不同，因而效用函数也有不同的类型，如下图所示：

图3 效用函数的类型Fig.3 Type of utility functions

其中曲线B为风险中性者的效用函数，即决策者的效用与投资收益呈线性关系。决策者对决策风险持中立态度，属中间型决策者，决策只需根据期望值作为选择的标准而不需要利用效用函数。曲线A为风险厌恶型效用函数，U''(w)<0呈凹性。表示效用随着期望值的增大而递增，但边际效用递减。决策者对利益的反应比较迟缓，对损失的反应则比较敏感，不求大利，但求规避风险，这是一种谨慎小心的保守型决策者。曲线中间部分呈上凹形状，表示决策者厌恶风险：上凹得越厉害，表示厌恶风险的程度越高。曲线C为风险偏好型效用函数，U''(w)>0呈凸性。表示效用随着期望值的增大而递增，且边际效用递增。决策者想获得大利而不关心亏损，即决策者对于亏损反应迟缓，对利益却很敏感，是一种想谋大利、不怕冒险的进取型的决策者。曲线的中间部分呈下凸形状，表示决策者喜欢冒险，敢于做大胆的尝试：效用曲线下凸得越厉害，表示冒险性越大[7-8]。

2 目标函数的建立

2.1 目标函数的建立

假定投资组合由股票、公司债券和国债组成，三种投资的比例分别为α1, α2, α3, 期望收益率分别为X1, X2, X3, ρij为第i种投资和第j种投资的相关系数，σi为第i种投资的标准差，i = 1, 2, 3，初始投资额为w0，假定投资组合的收益为一个随机过程dw(t)=µwdt+σwdB(t )，其中：B(t)为布朗运动；µw为投资组合收益率均值µ=αX+αX+αX；σw为投资组合收益率的标准差

w112233

同时，假定投资者为风险厌恶的，其效用函数为幂函数，其表达式为其中γ为风险厌恶系数，1<γ<+∞, w>0。这里请注意，虽然效用函数值为负数，但不影响对最优解的判断，这是因为负的效用值也有最优解。

2.2 历史数据的处理

本文以2004年、2005年、2006年、2009年和2010年5年间60个月的所有数据为基础（之所以剔除2007年和2008年的数据，是由于在种种原因的影响下，这两年间的数据波动极为剧烈，因此属于特殊年份的数据，不宜作为理论研究的基础；另外，采用月化的数据主要是考虑到方差及协方差计算的精确性，若采用年度数据，则会因数据太少而影响精确性）。根据上证综指的每日收盘价格、企债指数和国债指数的每日收盘价格及企业债和国债的月均收益率（全部经过向前复权处理）分别计算其平均收益率，计算结果如下：

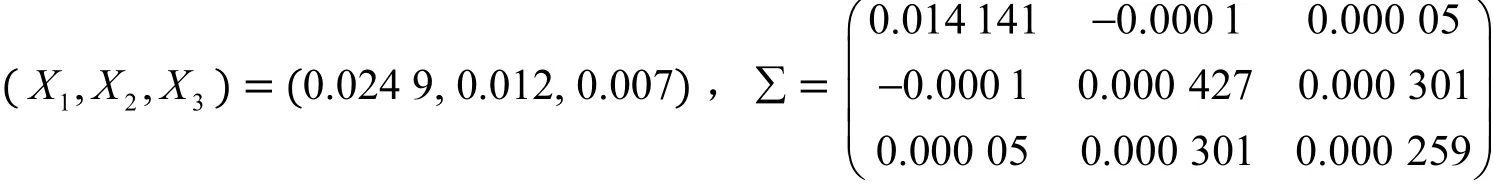
其中∑为协方差矩阵，行从左至右及列从上至下分别代表股票、公司债券和国债（数据来源为凤凰财经网）。

3 改变风险偏好和初始投资额时的最优投资组合选择

3.1 改变风险厌恶系数对投资组合的影响

在本节的内容中，首先分析风险厌恶系数改变对于最优投资组合的影响。为分析问题简单起见，我们假定初始投资额01w=。

由表1至表3可以看出，总体而言，VaR的约束值C越大，最优投资的组合方式越激进，反之，约束值越小，组合方式越保守。而在相同的VaR约束下，具有相对较高风险偏好的投资者，其风险厌恶系数较小，因此，其组合方式为更多地配置风险资产；相对而言，具有更低风险偏好的投资者，其风险厌恶系数则较高，因此将选择更为保守的策略，其组合方式为更多地配置低风险资产。

表1 幂效用函数下C = 0.2时改变风险厌恶系数对投资组合的影响Tab.1 Impact of portfolio when changing risk aversion coefficient with C = 0.2 under power utility function

表2 幂效用函数下C = 0.3时改变风险厌恶系数对投资组合的影响Tab.2 Impact of portfolio when changing risk aversion coefficient with C = 0.3 under power utility function

表3 幂效用函数下无VaR约束时改变风险厌恶系数对投资组合的影响Tab.3 Impact of portfolio when changing risk aversion coefficient under power utility function without constraint of VaR

由表1，在C = 0.2（即VaR＜ 0.2）的约束下，风险偏好较高的投资者（γ= 2），其最优投资的组合方式为将65 % 的资产配置为股票，25 % 的资产配置为公司债券，仅将10 % 的资产配置为国债，这种组合方式将为其带来更高的收益，但同时其承担的风险也更大；相对而言，对于风险偏好较小的投资者（γ= 6），其最优组合的方式更为保守，配置于股票的资产仅为40 % ，而配置于债券的资产达到60 % 之多。当一个投资者的风险厌恶系数达到10时，该投资者即表现出极度的风险厌恶特征，此时在他的组合中将不再有股票投资，其最优组合的配置方式为45 % 公司债和55 % 国债。

当进一步放宽VaR的约束，将C值定为0.3时，如表2所示，激进型的投资者将进一步提高风险资产——股票在整个投资组合中的配置，比例将占到75 % 之多，债券投资的比重仅为25 % 。而具有较小风险偏好的投资者（γ= 6的投资者），其组合的方式并未发生改变（理论上较C = 0.2时应更为激进，但由于数据的限制，实证结果较前者并未发生改变）；风险厌恶系数最高（γ=10）的投资者，在不进行股票投资的同时，又将部分低风险资产——公司债券的配置转移到了无风险资产——国债的配置上，显然更为保守。

最后，当不存在VaR约束的限制条件时，基于不同等级的风险厌恶系数，不同投资者的收益都将被最大化，但相对应的，其所承担的风险也最大，分析结果见表3。

3.1 同时改变初始投资额和风险厌恶对投资组合的影响

以上我们分析了风险厌恶系数改变对投资策略的影响，而由于初始投资对最优投资组合也会产生影响，下面我们就着重分析初始投资和风险厌恶系数同时改变时对投资组合的影响。

由表4至表8可见，从我们分析的结果来看，初始投资额的增大并不能保证其投资策略向更激进的方向发展。相反，当初始投资额大于1时，投资组合将随着投资额的增加而更偏保守。

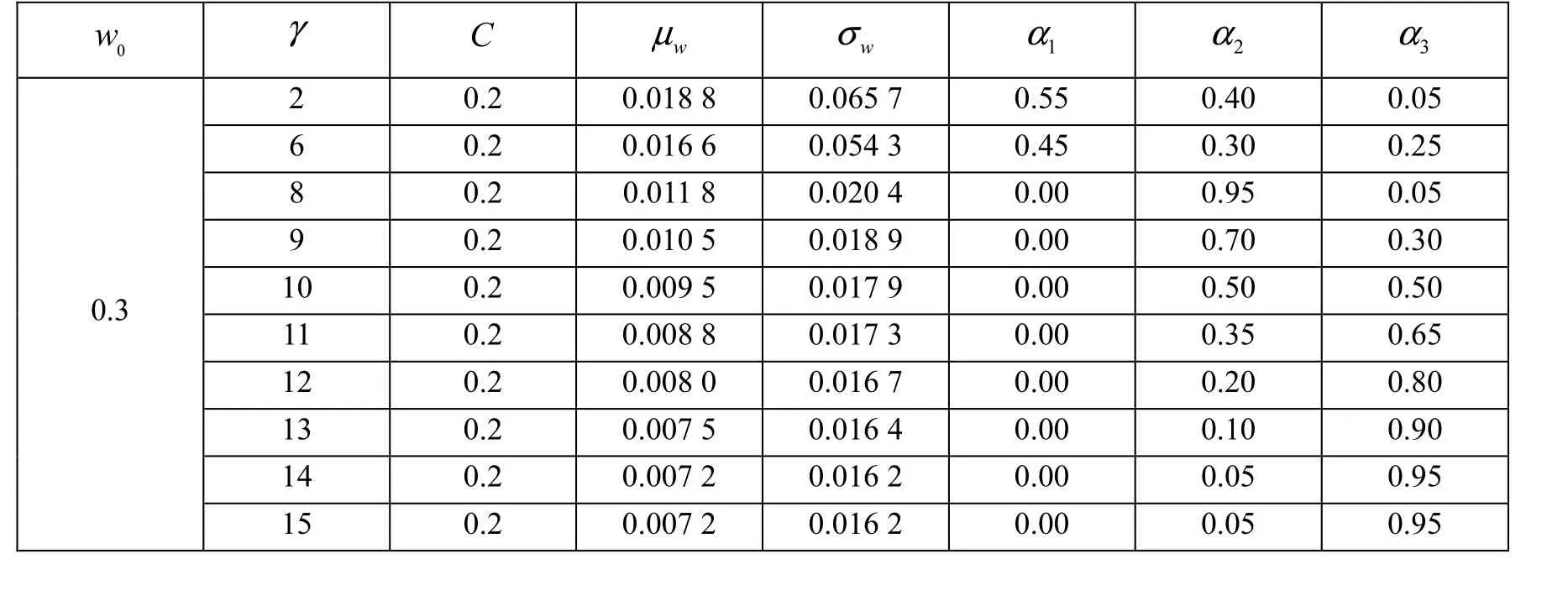
表4 初始投资额0w为0.3时改变风险厌恶系数对投资组合的影响Tab.4 Impact of portfolio when changing risk aversion coefficient with0w= 0.3

表5 初始投资额0w为0.5时改变风险厌恶系数对投资组合的影响Tab.5 Impact of portfolio when changing risk aversion coefficient with0w = 0.5

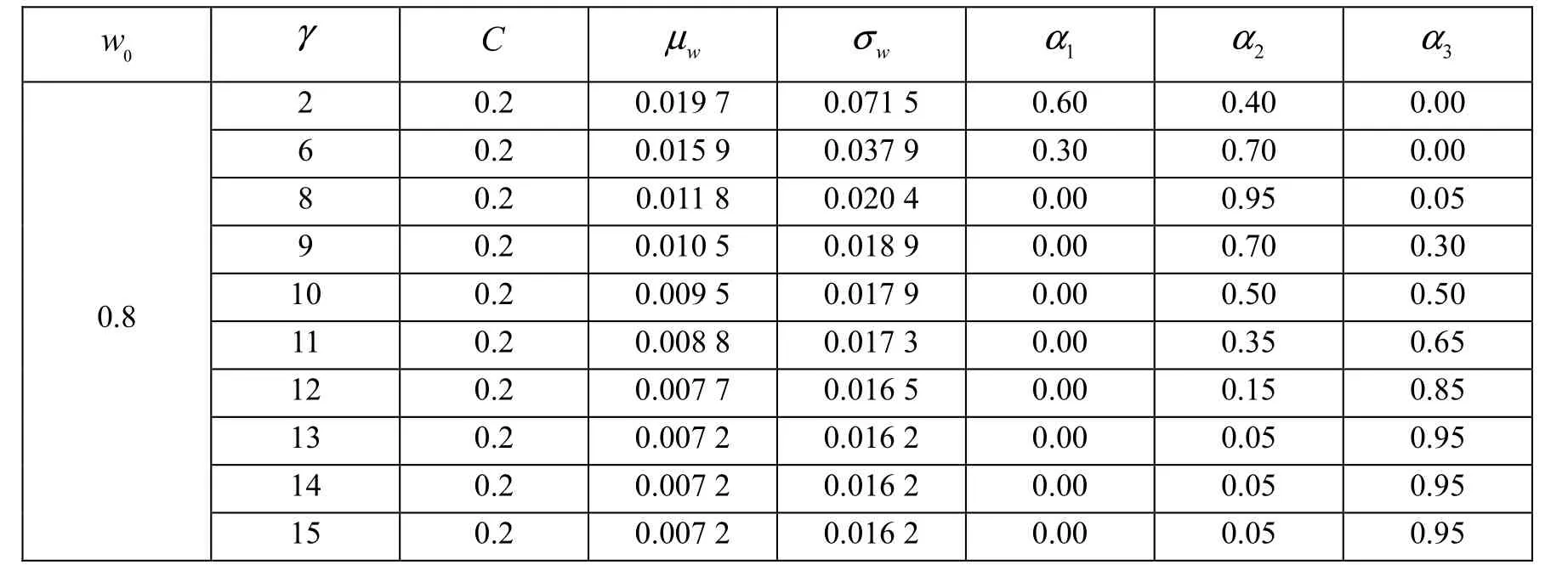
表6 初始投资额0w为0.8时改变风险厌恶系数对投资组合的影响Tab.6 Impact of portfolio when changing risk aversion coefficient with0w= 0.8

表7 初始投资额0w为1时改变风险厌恶系数对投资组合的影响Tab.7 Impact of portfolio when changing risk aversion coefficient with0w = 1

表8 初始投资额0w为10时改变风险厌恶系数对投资组合的影响Tab.8 Impact of portfolio when changing risk aversion coefficient with0w= 10

如：当风险厌恶系数γ= 6时，初始投资额0w= 1的投资者将40 % 的资产配置于股票投资，将60 % 的资产用于购买公司债券；当初始投资额由1上升为10, 50和100时，投资者则进一步降低了股票的投资，将5 %的配置由股票投资转移到了国债的投资上。

当风险厌恶系数γ= 11时，初始投资额0w= 1的投资者将全部资产用于债券投资，其中35 % 用于公司债券投资，65 % 用于国债投资；当初始投资额上升为10和50时，策略则更为保守，投资者将无风险资产——国债的比重调高至70 % ，将低风险资产——公司债券的比重在原有的基础上调低了5 % 。

当初始投资额0w小于1时，由表4至6可见，投资组合随财富值增大而发生的变化是不稳定的。

当γ= 2时，初始投资额0w= 0.3的投资者将55 % 的资产配置于股票投资，将45 % 的资产配置于公司债券，将5 % 的资产配置于国债；当初始投资额由0.3上升为0.5时，投资者变得更加激进，组合中取消了对无风险资产——国债的投资，将低风险资产——公司债券的配置上调至45 % ；当初始投资额进一步上升至0.8时，投资者又将公司债券中5 % 的配置转移到高风险资产-股票的配置中，投资策略更加激进。

当γ= 8时，在初始投资额0w= 0.3的情况下，投资者将95 % 的资产配置于公司债券的投资，将5 %的资产配置于国债；当0w上升为0.5时，投资策略变得更为激进，5 % 的国债投资配置将被转移到公司债券投资上；但当0w进一步上升为0.8时，投资者又变得保守起来，将公司债券投资的比重下调至95 % ，将国债投资的比重上调回5 % 。

当γ= 8时，也遇到了同样的情况，初始投资额为0.3的投资者将70 % 的资产配置于公司债券，其余资产投资于国债；当0w上升为0.5时，公司债券投资的比重被上调为75 % ，国债投资的比重相应减少；而当w0进一步上升为0.8时，配置方式又回到了w0= 0.3的情况。

当γ= 8时，在初始投资额0w= 0.3的情况下，投资者将20 % 的资产投资于公司债券，将80 % 的资产配置于国债投资；当初始投资额上升为0.5时，5 % 的资产配置由无风险资产——国债被转移到了低风险资产——公司债券的配置上，投资策略显然更为保守；当初始投资额由0.5上调至0.8时，投资者的策略又变得保守起来，有10 % 的资产从公司债券的配置被转移到国债的配置上。

综上所述，初始投资改变对最优投资组合会产生影响，而且初始投资的相对最大损失值和风险厌恶系数会同时影响最优投资组合。

4 结论

本文提出以投资者期望效用最大化为目标，以VaR不超过给定的常数为约束的最佳投资组合的确定，并以中国A股、公司债券和国债这三大证券在2004 ～ 2006年及2009 ～ 2010年间5年的历史数据为估计模型的参数值，借助于Matlab和Monte Carlo 模拟技术分析了各项参数改变对于最优投资组合的影响。分析结果证实了投资者对风险越是厌恶，投资策略就越趋保守；此外，发现初始投资和投资者对于风险的厌恶程度会同时影响投资者的投资策略。

[1] 鲁进勇. 现代资产组合理论研究[D]. 武汉: 武汉理工大学, 2004.

[2] Philippe Jorion 著; 陈跃等 译. 风险价值VAR[M]. 第2版. 北京: 中信出版社, 2004.

[3] 徐宝计. 基于VaR的投资组合风险度量模型分析[D]. 天津: 南开大学, 2009.

[4] 李振亚. 风险价值方法在证券投资组合风险管理中的一些应用[D]. 成都: 电子科技大学, 2008.

[5] 顾清. VaR方法在投资组合资产配置中的应用和实证检验[D]. 上海: 复旦大学, 2006.

[6] CAMPBELL R, HUISMAN R, KOEDIJK K. Optimal portfolio selection in a Value-at-Risk framework[J]. Journal of Banking & Finance, 2001, 25: 1789-1804.

[7] 李向科, 寂发全. 金融数学[M]. 北京: 中国人民大学出版社, 2004.

[8] 陈立文, 殷亮, 孙静. 效用理论在风险型投资决策中的应用[J]. 天津纺织学院学报, 2000, 19(6): 26-29.

[9] BRENTANI C. Portfolio Management in Practice[M]. London: Elsevier Butterworth-Heinemann Press, 2004.

[10] ELTON E J, GRUBER M J, BROWN S J, GOETZMANN W N著; 余维彬 译. 现代投资组合理论与投资分析[M]. 第7版. 北京: 机械工业出版社, 2008.

[11] REILLY F K, BROWN K C. Investment Analysis and Portfolio Management[M]. Six Edition. Boston: Harcourt College Press, 2002.

Optimal Selection of Investment Portfolio Based on Constraint of VaR

WEI Yi-hao, MAO Hong
(School of Economics and Management, Shanghai Second Polytechnic University, Shanghai 201209, P. R. China)

This paper presents the study on selection of optimal investment strategy which is based on the historical data of Chinese stock and bond markets from 2004 to 2006 and 2009 to 2010. The objective function of maximizing the expected utility with the constraint of Value at Risk (VaR) less than a constant was established. Stochastic simulation with the help of MATLAB was applied to analysis the investment portfolio selection of the investors with different degree of risk aversion. Finally, the feasibility of decreasing investment risk and providing steady income by using portfolio theory in China’s capital market was discussed.

VaR; portfolio; utility function; risk aversion; property; MATLAB

F832.33

A

1001-4543(2011)04-0298-09

2011-06-15;

2011-09-16

尉轶昊（1988－），男，上海人，在读大学生，主要研究方向为信用管理，电子邮箱 yihaowei@yahoo.com.cn。