高速铁路过渡段刚度最佳过渡方式研究

韦有信，钱小益，李成辉

(西南交通大学 土木工程学院，成都 610031)

目前，我国国内通用的过渡段做法是轨下基础刚度线性变化，这种过渡方式可以降低轨下基础刚度和沉降差异以保证行车平稳舒适并延长车辆和线路使用寿命，但是随着行车速度的不断提高，高速列车通过过渡段的时间也将 ＜1 s，这种情况下，过渡段的微小缺陷也将导致列车发生剧烈振动，从而引起轨道破坏。大量试验表明，高速列车通过过渡段时，轮轨动力作用明显加剧，直接影响到行车的平顺性和舒适性。因此，现行的刚度过渡方式不适合在高速铁路中使用，应该考虑采用其他的刚度过渡方式。本文将运用有限单元法建立过渡段的力学模型，通过对比几种不同刚度过渡方式在相同荷载下的钢轨状态和基础反力，分析现行过渡段出现问题的原因，选出过渡段刚度的最佳过渡方式。

1 力学模型

该过渡段模型全长为26.4 m，低刚度端与高刚度端长度均取为3 m，过渡段长度取为20.4 m，扣件间距为0.6 m。为使得分析结果明显，轨道两端刚度比取为1∶4，低刚度取20 kN/mm，高刚度取80 kN/mm。荷载P取车辆总荷载的1/4，约取130 kN。过渡段简化模型见图1。

本模型中选用3种过渡段刚度过渡方式进行对比分析。3种刚度过渡方式分别为线性过渡、正弦曲线过渡和抛物线与三次多项式组合曲线过渡，轨下弹簧刚度的具体计算如下:

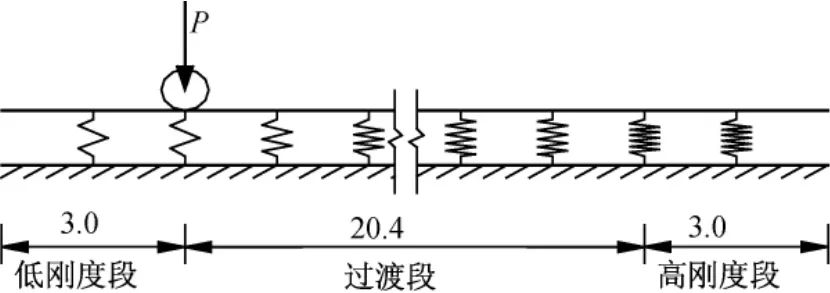
图1 过渡段模型(单位:m)

设x为模型中各点距左端点的距离。x介于0～3.0 m(包含3.0)时，轨下弹簧刚度为20 kN/mm;x介于3.0～23.4 m时，过渡方式有三种。

1)线性过渡

轨下弹簧刚度为

2)正弦曲线过渡

设轨下弹簧刚度为

3)组合曲线过渡(抛物线和三次多项式组成)

设模型中各点距左端点的距离 x∈(3，18.6］时，组合曲线为抛物线，轨下弹簧刚度为

设x∈(18.6，23.4)时，组合曲线为三次多项式，轨下弹簧刚度为

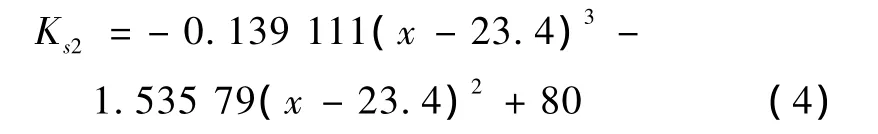
x介于23.4～26.4 m时(包含23.4)，轨下弹簧节点刚度为80 kN/m。

过渡段具体刚度形式见图2。

2 计算分析

图2 过渡段刚度曲线图

对模型上各弹性支撑点分别作用车辆荷载P，得出钢轨上各弹性支撑点在车辆荷载P作用下的钢轨垂向位移图(见图3)、钢轨垂向位移变化率图(见图4)和荷载作用点下的基础反力图(见图5)。

图3 钢轨垂向位移图

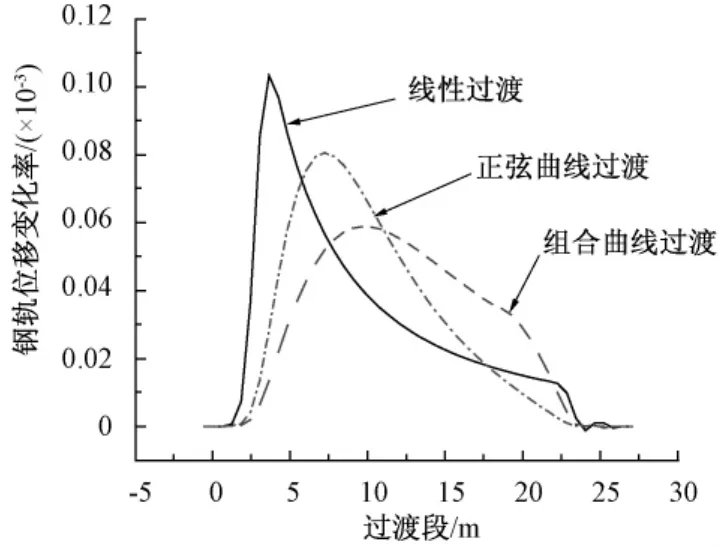
图4 钢轨垂向位移变化率图

图5 荷载作用点下的基础反力图

2.1 钢轨状态

刚度采用线性过渡时，钢轨变形曲线并非呈线性过渡，而是呈向上凸起的曲线，受此影响，列车在运行至低刚度端时，钢轨垂向位移发生较大变化，列车高速通过时，轮轨动作用力将明显增大，由于该位置钢轨垂向位移变化率最大且发生突变，所以轮轨动作用力的最大值也往往发生在该位置，这将直接影响列车运行的平顺性和舒适性。由此可见，过渡段低刚度端接头依然是行车速度的一个控制因素。刚度采用正弦曲线过渡时，在低刚度端，钢轨垂向位移曲线过渡较为平缓，且消除了线性过渡情况下的钢轨垂向位移变化率突变，列车荷载作用下的钢轨状态得到很大改善，但就整体而言，钢轨曲线坡度依然较大。相对前述两种过渡方式而言，刚度采用组合曲线过渡的时候，钢轨最大垂向位移变化率最小，且变化平缓，就整体而言，荷载作用下的钢轨曲线坡度最小，钢轨状态最为理想。

从钢轨状态的角度来看，在相同荷载作用下，现行的过渡段刚度线性过渡情况下的轨道状态最不理想，主要是因为荷载作用下的钢轨曲线上凸，且在过渡段接头处存在刚度突变。采用其他两种曲线过渡的时候，轨道状态要理想得多，特别是采用抛物线与三次多项式组合曲线过渡时，钢轨垂向位移曲线坡度最小，且在过渡段两端处，钢轨垂向位移曲线更为平缓。

2.2 基础反力

轨下基础反力与过渡段轨下刚度成正比，随着过渡段轨下刚度增大，基础反力逐渐增大，与低刚度端相比，高刚度端基础反力值增幅达50%。由图5可知，线性过渡的基础反力在过渡段接头处发生突变，列车行至此处，会对轨道造成一定冲击，引起轨道破坏，这主要是由于刚度突变所造成的，在过渡段低刚度端接头处，荷载作用点下弹簧刚度要小于两侧节点刚度的平均值，受钢轨抗弯刚度的影响，荷载作用点下两端节点将承担更大部分的荷载。由此可知，刚度突变是导致过渡段端点处基础反力突变的根本原因。实际轨道中设置辅助轨(一对、两对)或采用梯形轨道过渡就是通过加大轨排抗弯刚度，使轨下基础受力均匀，并最大限度地减小沉降差，使轨道保持良好状态。从图5中还可看出，由于组合曲线过渡形式中的刚度没有突变，所以消除了线性过渡的基础反力突变，且从整体上看，组合曲线的基础反力要小于其他两种过渡方式，轨道的受力比其他两种情况更加均匀。

从基础反力的角度来看，过渡段刚度采用组合曲线过渡要明显好于采用其他过渡方式，不仅消除了线性过渡情况下的基础反力突变，而且其轨下基础反力亦明显小于其他几种过渡方式。

3 结论

现行的线性过渡在荷载作用下的钢轨状态并不是成线性变化，而是向上突起。而且过渡段采用线性过渡的时候，在过渡段两端接头处依然存在刚度突变的问题，这些问题导致钢轨垂向位移曲线不平顺，轨下基础反力发生突变。相对线性过渡而言，正弦曲线过渡则减缓了过渡段接头处钢轨不平顺的问题，且消除了轨下基础反力突变的现象。抛物线与三次多项式组合曲线过渡相对以上两者而言，则有更好的改进，它极大地减缓了过渡段接头处的钢轨不平顺问题，还消除了过渡段接头处的基础反力突变。从整体而言，组合曲线过渡情况下，不仅钢轨垂向位移曲线最为平顺，而且其基础反力分布也最为均匀。由此可知，目前的线性过渡方式并不是过渡段刚度过渡的最佳方式，采用组合曲线过渡的效果将会明显好于采用其他过渡方式。

［1］李成辉.轨道［M］.成都:西南交通大学出版社，2007:7-34.

［2］郝瀛.铁道工程［M］.北京:中国铁道出版社，2004:10-41.

［3］王小韬.轨道过渡段动不平顺分析［D］.成都:西南交通大学，2007.

［4］雷晓燕.轨道过渡段刚度突变对轨道振动的影响［J］.中国铁道科学，2006，27(5):42-45.

［5］崔国庆.双块式无砟轨道合理刚度取值研究［J］.铁道建筑，2009(9):93-96.

［6］詹学启，郭建湖.武广铁路客运专线乌龙泉至韶关段无砟轨道路基过渡段设计［J］.铁道建筑，2010(1):106-110.