大体积混凝土底部的弹性约束试验研究

李潘武，边 真，高向东

(1.长安大学 建筑工程学院，西安 710061;2.中国市政工程华北设计研究总院 西安分院，西安 710018)

在大体积混凝土结构的施工中，由于混凝土标号高、水泥用量大，所以混凝土内部由于水泥熟化释放大量的水化热而又不能及时排出时造成混凝土的高温，混凝土产生膨胀，而后由于混凝土散热，混凝土开始收缩。在大体积混凝土的收缩过程中，由于混凝土受到底部地基或结构的约束，使混凝土内部产生很大的拉应力及过大的拉应变，当拉应力超过混凝土的抗拉强度时，混凝土开裂［1-4］。大体积混凝土开裂防治问题一直影响着土木工程施工，就其解决办法，国内外学者提出了很多方法［5-9］，但都无法根治。本文在前人研究的基础上做出了新的尝试，为了减少混凝土的拉应变，在大体积混凝土的膨胀过程中，设置约束机制，限制混凝土的膨胀率，减少混凝土的拉应变，使混凝土的裂缝不集中发生在某处，从而减少了可观裂缝。

1 设“抗、放”结合的弹性约束机制

在大体积混凝土结构的施工中，由于混凝土的温度升高而使其产生体积增大和由于降温而产生体积缩小的变化过程及在此过程中产生的压、拉应力变化。如果混凝土内部温差过大，则使混凝土内部产生过大的拉应变，当拉应变过大时，可能造成混凝土开裂。为了减少这种拉应变，在大体积混凝土的底部设置弹簧约束，使混凝土在温度升高产生膨胀时受到弹簧的弹性约束(同时弹簧伸长)，从而减少了混凝土的压应变。当混凝土内部温度下降开始收缩时，弹性力又将使混凝土的拉应变减少，从而降低混凝土的收缩应力，具体分析如下所述。

1.1 模型建立

如图1所示置于地面上的大体积混凝土结构，设其为长方体:高h，长LX，宽 LY。在大体积混凝土的底部通过预留孔洞置放抗拉钢杆(钢杆断面积为 Ar，弹性模量为Er，钢杆表面涂绝热材料)，抗拉钢杆的数量设计见后。

图1 抗、放结合的弹簧约束

在钢杆的两边通过弹簧(弹簧的刚度为K，弹性模量为Ee)约束，此时有

式中，ε1为结构实际变位;αT为结构自由变位，其中，α为混凝土线性膨胀系数，可取为0.000 01/℃;T为综合降温差;ε2为结构约束变位。ε2=σ/E，其中，σ为约束体的应力，σ=E(ε-αT)/(1-μ)，E为约束体弹性模量，μ为约束体的泊松比。

根据直法线假定，ε应为 z(厚度方向)的线性函数。

其中，u，υ分别为坐标 X，Y方向的位移。

将ε代入σ中，有

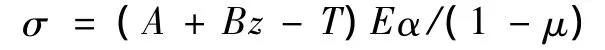
式中，A，B为与坐标z无关的参数。

1.2 温度应力的计算

1.2.1 弹性温度应力

假定混凝土四周是刚性的，在 X，Y两个方向，板受到完全约束，应变为零，即 εx=0，εy=0;对应的应力分别为σx，σy。在Z方向，板没有承受荷载，也可以自由变形，因此Z方向的正应力应等于零，即σz=0。

根据广义虎克定理，有(当弹性模量为常数时)

实际上混凝土的弹性模量是随着龄期而变化的。为了考虑这一重要因素，采用增量法计算混凝土温度应力［10］，把时间划分为一系列时段:Δti，i=1，2，…，n。在第 i时段 Δti内的温度增量为

由温差ΔTi引起的弹性温度应力增量Δ为

1.2.2 弹性徐变温度应力

弹性徐变温度应力σ(t)为

式中，k(t，τ)为松弛系数，

1.2.3 约束对温度应力的影响［11-12］(弹性约束)

其中定义 ε2x=(σx-μσy)/E 及 ε2y=(σy-μσx)/E分别是X、Y方向约束应变。

定义 R(x)，R(y)分别是 X、Y方向约束度，且 R(x)=ε2x/ε1，R(y)= ε1x/ε1。

约束度的正、负号关系能反应实际应变的大小及混凝土的开裂程度。当约束度为负值时，即约束应力产生的变形与混凝土产生的自由变形的方向相反。

如本模型(图1)中，当混凝土内部温度升高时，混凝土产生膨胀，其自由膨胀应变 ε1= αT［13-14］，变形ΔLx= αTLx。

当混凝土施加弹性力受到约束时，自由膨胀受到限制，约束变形为负。

约束度在本模型中其值为-1≤R≤0。

当R=-1时，为全约束状态，混凝土的实际变形为零(即实际应变等于零);

当R=0时，为自由变形状态，混凝土的实际变形为最大(即实际应变等于自由应变);

当-1＜R＜0时，为弹性约束，此时混凝土的膨胀变形值等于弹簧的压缩变形值加钢拉杆的拉伸变形值，即

式中，S为混凝土的膨胀变形值或弹簧的压缩变形值加钢拉杆的拉伸长度，εh为混凝土的应变，Lh为混凝土的长度，εe为弹簧的压缩应变，Le为弹簧的长度，Ll为拉杆的长度等于混凝土的长度Lh，K为弹簧的刚度系数，P为弹簧所受到的最大约束力，A为钢拉杆的横截面面积，Er为钢拉杆的弹性模量。

混凝土X、Y方向实际应力σx、σy分别为

式中，Eh为混凝土的弹性模量;μ为混凝土的泊松比;Lxh为混凝土 X方向的长度;Lyh为混凝土 Y方向的长度;Px，Py分别为弹簧所受X，Y方向的约束力。

1.3 弹性约束中的弹簧数量及弹性应变

1.3.1 X，Y方向的弹簧数量

X，Y方向的弹簧数量分别为

式中，h为混凝土的厚度;Lxh，Lyh分别为混凝土的 X，Y方向的长度。

1.3.2 混凝土的约束应变

混凝土的约束应变ε2x(y)为

混凝土的约束变形S为

当混凝土膨胀无约束时

当混凝土受到完全约束时

此时，K，Er=∞ 。

式中，σx(y)为Y方向约束下混凝土在X方向产生的应力;σy(x)为X方向约束下混凝土在Y方向产生的应力;Px(y)为Y方向约束下弹簧所受到的X方向最大约束力;Px(y)为X方向约束下弹簧所受到的Y方向最大约束力;Lx(y)为Y方向约束下混凝土在X方向的长度;Ly(x)为X方向约束下混凝土在Y方向的长度。

当混凝土温度升至最高时，混凝土受到的压力最大。但随着混凝土内部温度的降低，混凝土开始收缩。此时，弹簧伸长，压力减小，钢杆收缩变短。在此期间，由于混凝土的弹性模量增大，混凝土无法复原至原来浇筑时的几何尺寸。但由于存在弹簧的压力和钢杆收缩力，克服了部分混凝土体与地基之间的摩阻力，使混凝土的拉应力降低。

由于弹簧与钢拉杆收缩产生的压应力所克服的约束力为nx(y)Px(y)。

实际上相当于混凝土的收缩应力减小了nx(y)Px(y)/(Lx(y)h)。

2 试验与试验结果［15］

2.1 试验

制作强度为C40、断面尺寸为1 200 mm×1 200 mm×1 000 mm的大体积混凝土试件2块(内部均埋设温度和应变测试器件)，试件置于试验室混凝土地面上，其中一试件在底部施加水平压力(简称试件1)，另一试件不施加水平压力(简称试件2)。两试块底部均与混凝土地面之间铺设1 mm厚的油毡一层。加压系统，如图2所示。

图2 加压系统(单位:mm)

混凝土灌注24 h后，开始分级施加压力，每级荷载2 kN，稳定1 h。当荷载加至96 kN，并稳定1 h后，直接加至150 kN，再稳定1 h后，加200 kN，稳定18 h，开始卸载，每20 min卸一级荷载，每级荷载20 kN。

2.2 试验结果

2.2.1 混凝土试件应力、应变的分布曲线

1)加压前试件底部中心线上应变应力分布曲线如图3。

2)加压时试件底部在加压方向中心线(半长)的应变、应力分布

以下所有图中，实线及虚线分别表示试件1、试件2的应变(×10-6)或应力(×10-2MPa)。其中，正值表示拉，负值表示压。横轴表示测点，纵轴表示应变或应力。

①加载50 kN时(相当于局部表面压应力为18.95×10-2MPa)的应变、应力，见图4。

图3 试件底部中心线上各测点最高温度时的应变、应力分布曲线

② 加载200 kN，并持荷14 h后(相当于局部表面压应力为75.8×10-2MPa)的应变、应力，见图5。

3)底部中心点处加载、卸载过程的应变与荷载的关系，见图6。

图4 加载50 kN时的应变、应力曲线

图5 加压200 kN、持荷14 h后的应变、应力曲线

图6 试件1底部中心点处加载、卸载过程的应变与荷载曲线

2.2.2 试验结果

从以上试验资料可以知道，随着试件底部压力的增大，试件底部的拉应力及拉应变逐渐变小，当试件底部施加的局部表面压应力增加至75.8×10-2MPa时，试件底部由拉应力转变为压应力。这说明在试件底部增加压力可以有效地降低其底部的拉应力，从而降低混凝土开裂的可能性。

3 结论

从以上理论和试验资料分析可知，对大体积混凝土结构通过施加约束压应力，可以有效地减小混凝土的收缩应力(拉应力)，降低混凝土的收缩应变(拉应变)，从而使混凝土的抗裂性能提高。另外，从前述可以看出，随着弹簧刚度及弹簧数量或底部压应力的增大，混凝土的弹性应变也将减少，从而也使混凝土的抗裂性能提高。在工程实际中，弹簧可以用预应力钢筋来替代。

［1］朱伯芳.大体积混凝土的温度应力与温度控制［M］.北京:中国电力出版社，1999.

［2］杨和礼.基础大体积混凝土的裂缝控制［J］.武汉大学学报(工学版)，2007(10):74-76.

［3］冯乃谦，顾晴霞，郝挺宇.混凝土结构的裂缝与对策［M］.北京:机械工业出版社，2006.

［4］叶成杰.大体积混凝土抗裂性能研究［J］.四川建筑科学研究，2010，36(2):237-238.

［5］江昔平.超大大体积混凝土温度裂缝产生机理与抗裂控制新对策［J］.混凝土，2007，218(12):98-102.

［6］PRICE WALTER H.Control of cracking in mass concerete Dams［J］.Concrete Internation，1982，4(10):34-36.

［7］SADAMU O.Thermal cracking control in Mass Concrete［J］.Proceedings of the fourth International Conference on Materials Engineering for Resources，2001(4):34-36.

［8］夏锦江.大体积混凝土温度裂缝防控措施［J］.河南大学学报(自然科学版)，2008，38(4):437-439.

［9］ANON.Control of cracking in concrete structures［J］.Concrete Internation，1980，2(10):75-76.

［10］YOSHIDA H，SAWADA T.Analytical study on the thermal strees of mass concerete［J］.Transactions of the International Conference on Structural Meachanics in Reactor Technology，1983，5(21):109-117.

［11］ISHIKAWA，MASAMI.Effect of extermal restraint of mass concrete［J］.Proceedings of the Japan Society of Civil Engineers，1993，15(460):13-22.

［12］王铁梦.工程结构裂缝控制［M］.北京:中国建筑工业出版社，1997.

［13］汪国权.大体积混凝土裂缝及温度应力研究［D］.合肥:合肥工业大学，2006.

［14］富文权，韩素芳.混凝土工程裂缝分析与控制［M］.北京:中国铁道出版社，2003.

［15］李潘武.大体积混凝土试验报告［D］.西安:长安大学，2004.