基于模糊理论的边坡失稳风险评估研究
2011-09-03王禹
王 禹
(沈阳铁道勘察设计院有限公司,沈阳 110013)
1 概述
边坡的失稳破坏对工程稳定、交通运输及人民的生命财产安全造成巨大的危害,滑坡已经和火山、地震并列为三大地质灾害源[1]。我国由于地质和施工不善等因素导致边坡失稳事故时有发生,使得边坡稳定性问题成为我国近年来热点、难点问题之一。为了尽可能减少和避免边坡失稳风险事故的发生,有必要对边坡失稳风险进行深入研究,实现边坡失稳风险的有效评估与管理。国内外许多学者对岩土工程的风险展开了研究,并取得了一些重要成果。
边坡失稳风险因素复杂,主要包括地质地貌、动力环境以及人为因素。这些因素都具有较大的不确定性,一般应是一个模糊区间,而非是一个实数[2],同时由于评价结果也具有模糊性,因此,运用模糊区间来描述风险更能符合实际情况。笔者利用模糊理论对边坡失稳风险进行识别评价,并结合工程实例进行分析应用,以期更有效地评估边坡的安全稳定性。
2 边坡失稳风险管理
边坡工程失稳风险管理流程如图1所示,一般包括风险计划、风险评估和风险控制三个阶段[3]。首先,应制定安全风险管理计划,确定安全风险管理目标和风险接受准则,是实行风险管理工作的前提。其次,风险评估阶段是认识风险发生的本质,采取定量、定性相结合的方法得出风险分析结果的过程,需建立边坡失稳风险评价体系,结合专家调查法、层次分析法赋予权重系数,基于专家给出的概率估值利用模糊隶属函数对各评价指标进行置信区间估计,得出边坡失稳风险的风险度区间。最后,风险控制阶段是对风险进行处置、监控的过程,需根据风险接收准则对风险评估结果制定相应的风险应对措施,使失稳风险始终处于可接受程度。

图1 失稳风险管理流程

式中,当 n 取 4,2,1,0.5,0.25 时,f(u)分别描述“极接近(VVC)”、“非常接近(VC)”、“接近(C)”、“有点接近(FC)”、“略接近(FFC)”,f(u)=1时表示“完全接近(AC)”;u是隶属函数曲线的横坐标;a则是按照取对数原则计算得来。利用以上计算原则可绘制出描述“接近0.26”隶属函数曲线如图2所示。
3 边坡失稳风险评估
3.1 模糊理论
边坡失稳致险因素纷乱复杂,且难以用数字来精确地加以定量衡量,但都可以根据专家的经验和知识用语言定性地描述其性质及其可能产生的影响,故利用模糊理论中的模糊隶属函数来度量该类风险是具有现实意义的。美国学者 Zadeh[4]于1965年首次提出表达事物模糊性的重要概念——隶属函数,从而突破了经典集合理论,奠定模糊理论的基础。隶属函数的定义是确定一个对应函数使模糊论域到[0,1]闭区间的任一映射都能确定一个模糊子集。该对应函数称为模糊子集的隶属函数,也是该子集的隶属度。
(1)模糊隶属函数
本文采用文献[5]中的隶属函数“接近于”来描述专家对估计值的确信程度,如式(1)所示

图2 描述“接近0.26”模糊隶属函数曲线
(2)模糊区间
利用专家的专业知识以及多年积累的工程经验对工程项目的风险进行主观评判可实现风险的定性分析;基于历年风险事故统计数据,采用统计方法或者数值模拟对风险进行定量的估算可实现风险的定量分析;在定性分析的基础上进行定量的计算则可实现风险的半定量分析。风险的模糊性特点决定了风险度很难用具体的数值来加以衡量,并且底层风险评价集的获得是建立在专家主观判断的基础上,故结合隶属函数曲线对评价结果确定一个表示可信程度的模糊区间,能更合理地描述风险。影响专家主观判断的因素包括风险事件的复杂程度和专家的受教育程度、经验,影响概率参数估计效果的因素包括数据的可靠性、完整性和概率分析方法的适用性。根据表1可确定专家估值的确信程度,然后根据图2选择相应的模糊隶属函数曲线,再通过求解模糊曲线的λ截集[6]来确定风险的模糊范围。即在取置信水平为λ时,模糊区间的上限和下限分别为隶属函数曲线与直线f(u)=λ的两个交点的横坐标。
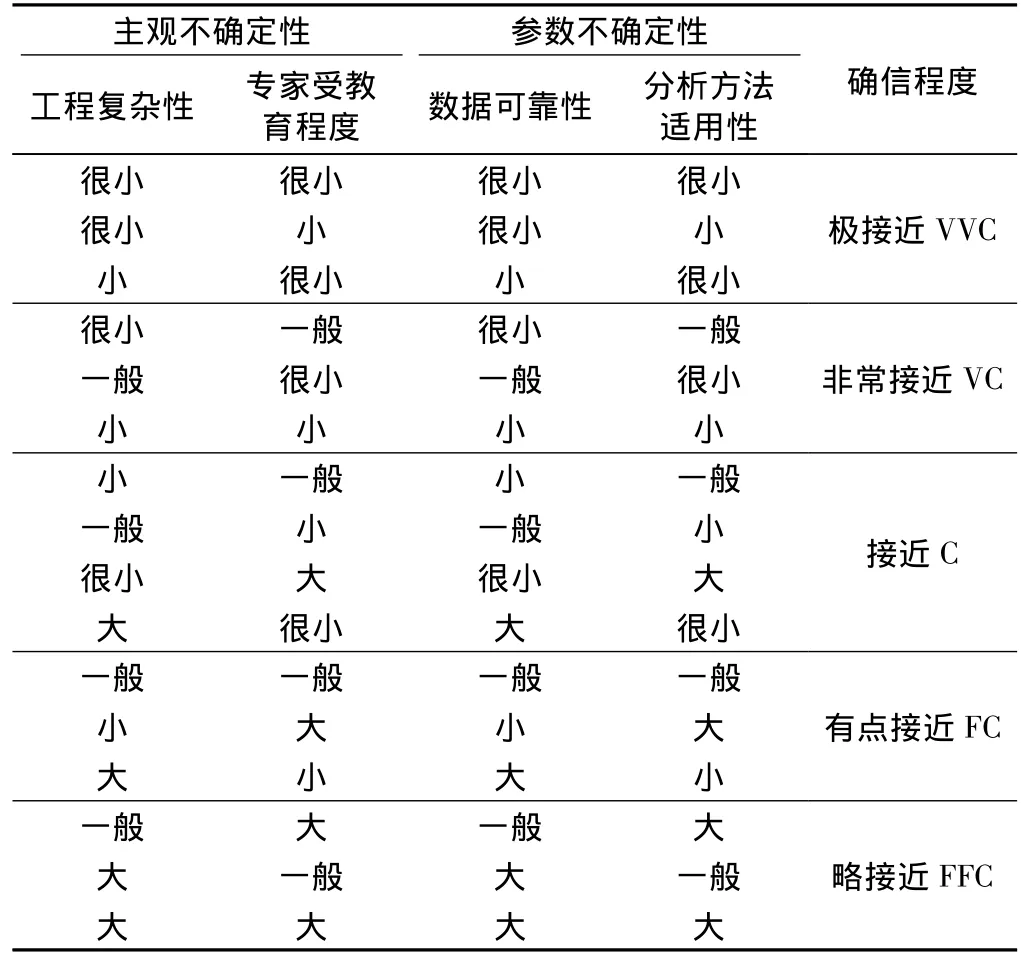
表1 专家估值确信程度判断标准[5]
3.2 风险评估
根据风险的定义,并参考文献[3],风险度R取决于风险事故发生概率P和损失C,其关系可表示为R=P+C。由此可知地下工程安全风险的评价应包括概率和后果两方面的估算。
风险概率的计算需要先建立相应风险评价指标体系,再利用AHP计算各指标之间的权重系数,然后按照式2计算出失稳风险概率值,最后进一步给出其模糊区间。

式中,Pi表示上层风险因素概率值;Pij表示下层风险因素概率值;ωij表示第i层第j个风险因素的权重系数。风险后果需要专家根据专业经验及知识评价出可能的后果值,再进一步计算出其模糊区间[Rmin,Rmax]。
3.3 风险管理标准
边坡失稳风险管理需要预先制定明确的风险管理计划、目标及其准则,由于边坡失稳风险目前还没有出台系统的管理标准及相关法律法规,故前期主要借鉴隧道、基坑等相关研究成果[3,7],在经过长期工程实践及事故统计后,本文给出了边坡失稳风险的概率估值、后果估值和风险接受准则,分别如表2~表4所示。

表2 概率估值标准

表3 后果估值标准

表4 风险接受准则
4 工程实例
4.1 工程概况
重庆某铁路边坡工程位于重庆某新建铁路DK15+350段,边坡高程945~1 005 m,呈鼻梁状凸形坡地貌。边坡平面形态呈上窄下宽的长条状,纵长115 m,前缘横宽82 m,后缘横宽10 m,边坡分布面积4.9×103m2,软弱面最大埋深 10~15 m,体积 4.0×104m3,路基边坡坡高大于4 m。该边坡土体结构松散,粘结力小,透水能力强,岩相复杂而多变,该处地表水及山坡上方地下水补给较丰富。由于该边坡土质主要由泥岩、砂岩块、碎石、角砾、砂及粉质黏土等不同时期、不同成因的堆积物质交错重叠而成,且这些物质在很短距离内先后出现并相互交错,从而导致剖面上不同土层间渗水性、富水性差异,造成可能滑动面复杂,失稳风险较大。
4.2 风险评估
(1)风险辨识
风险评价指标体系是整个风险评估的基础,对整个风险评估工作起着决定性作用,所建立的风险评价指标体系应该具有系统性、科学性、客观性和可操作性。本文在广泛调研、长时间现场实践应用的基础上,建立了以边坡失稳为目标风险的评价体系,并结合专家调查,利用AHP进行一致性检验并得出权重系数,如表5所示。

表5 边坡失稳风险评价体系及计算结果
(2)风险评价
①底层风险因素的概率等级以及风险后果等级需要利用专家调查法得到,由于同一评价单元会有多个专家参与评价,所以需要根据各参与专家的资历、经验、职称等因素确定其影响权重,然后按照该权重统计各专家意见,得出各事件的概率和后果的评价值。
②根据工程的复杂性、专家经验、数据的可信度以及分析方法的可行性,结合查阅表1确定专家估值的确信程度,评估时可结合各专家情况综合确定估值确信程度。如表5中“地质地貌—岩性”因素诱发失稳发生概率估值为0.63的确信程度为“接近(C)”,同理可得其他事件评价结果(表5、表6)。
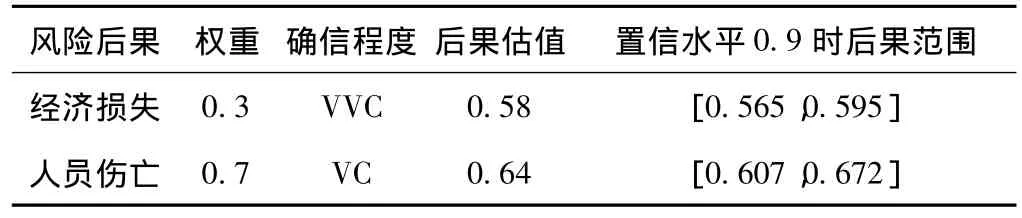
表6 边坡失稳后果权重、估值及范围
③取置信水平λ=0.9,则模糊区间的最小值和最大值分别为隶属函数曲线与直线f(u)=0.9的两个交点的横坐标。如“地质地貌—岩性”因素的描述为“接近(C)0.63”,故取 n=1,计算出 a=0.666 6,结合 f(u)=0.9作出λ截集,得到Pmin=0.567,Pmax=0.690,即该风险事件置信水平为0.9时的概率范围为[0.567,0.690]。同理可计算出其他事件的概率范围和后果范围(表5、表6)。
④按照式2和表5求得边坡失稳总风险发生概率估值 P=0.525,模糊区间为[0.474,0.573],风险后果估值 C=0.622,模糊区间围为[0.594,0.622],最终计算出风险度 R=1.147、Rmin=1.069、Rmax=1.222。
4.3 风险控制
该边坡失稳风险度为1.147,在置信水平 λ=0.9时模糊区间为[1.069,1.222],根据表4,可知该失稳风险等级为3,为不期望范围,需要引起重视,采取合理有效的风险处理措施并加强监测,及时降低风险至可接受水平,使生产生活安全得以保障。具体风险应对措施如下。
(1)刷坡
由于该路段土体结构松散,且风险分析结果显示地质地貌中岩性和坡度对风险度影响较大,故应先采取刷坡以清除坡面危岩、严重风化破碎表层及不稳定部分,清除影响边坡及边沟的坡脚坍塌堆积物、风化剥落碎屑物等,其目的在于调整边坡表层土质结构,增强边坡自稳能力。
(2)截排水
该地区降雨丰富,边坡又近接河流,风险评价结果显示出降雨和河流对边坡失稳风险贡献较大,故应采取合理的截排水措施。工程中在边坡顶设截水沟,底宽0.6 m,深0.4 m。坡面每隔1~2 m上下左右交错设置0.1 m×0.15 m矩形泄水孔。最下一排泄水孔高出路肩0.3 m,路基两侧设矩形侧沟,底宽0.6 m,深1.0 m,两侧留1.0 m宽侧沟平台。侧沟外侧沿线路纵向设φ100 mm塑料盲沟管,每隔10 m设一根长1 m的φ100 mm塑料盲沟管插入侧沟泄水孔向沟内排水。以上截排水措施对防治边坡坍塌有良好的效果,实践表明,凡采取该措施的路段边坡稳定性都很好。
(3)边坡防护
由于表层土体风化强烈,虽通过刷坡清除了危岩等,但为防止后期边坡开挖后表层加速风化,产生剥落、零星坠石等现象,可采用水泥砂浆封面、护面等措施,也可用施作支护墙,既可防护坡面,又能起支撑作用。工程中该段边坡坡面采取全坡面水泥砂浆砌片石护墙防护,侧沟、侧沟平台和护墙砌为一体。由于该地区夏季易发生暴雨,施工最好安排在旱季进行,以保障施工进度和质量。
5 结论
(1)通过工程实践表明,利用模糊理论和专家调查,通过模糊隶属函数确定风险事件的模糊区间是合理的,且符合工程实际的。
(2)依据建立的风险评价体系及其理论对边坡失稳风险进行评估是合理可行的,能较客观的评价出该类风险,为制定有效的风险应对措施提供理论依据。
(3)本实例中边坡失稳风险等级为3,位于不期望范围,故针对主要风险源采取了合理的风险应对措施,实践表明该措施取得了不错的成效,可为同类工程所借鉴。
[1]Christopher R.J.Kilburn,David N.Petley.Forecasting giant,catastrophic slope collapse:lessons from Vajont,Northern Italy[J].Geomorphology,2003(54):21-32.
[2]Zadeh L.A.The role of fuzzy logic in the management of uncertainty in expert systems[J].Fuzzy Sets and Systems,1983,11(1/3):197-198.
[3]中华人民共和国铁道部.铁建设[2007]200号 铁路隧道风险评估与管理暂行规定[S].北京:中国铁道出版社,2007.
[4]Zadeh L.A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[5]CHO H.N.CHOI H.H.KIM Y.B.A risk assessment methodology for incorporating uncertainties using fuzzy concepts[J].Journal of Reliability Engineering and System Safety,2002,78(2):173-183.
[6]秦寿康.综合评价原理与应用[M].北京:电子工业出版社,2003.
[7]边亦海,黄宏伟,李剑.可信性方法在深基坑施工期风险分析中的应用[J].地下空间与工程学报,2006,2(1):70-73.
