一种基于KPCA和形状先验知识的图像分割模型
2011-09-02万小萍重庆大学生物工程学院重庆400044
万小萍 顾 勇(重庆大学生物工程学院,重庆 400044)
2(重庆警官职业学院,重庆 400039)
引言
图像分割是图像处理过程中具有挑战性的关键步骤,其目的在于将一幅图像按照一定的特征(如颜色、纹理等)分成若干有意义的互不交叠的同质区。在各种分割方法中,由Kass等在1988年提出的可变形模型[1],由于其能很好的分割出兴趣目标的形状,近年来成为图像分割中最常用的方法之一。可变形模型在许多场合都能得到满意的结果,但是在有些情况下,如图像中存在大量的噪声、目标物体有缺损或含有错误信息时,大部分不含先验知识的算法都很难得到有意义的分割结果。
此时要想得到满意的分割结果,其中一个比较好的解决办法是在分割过程中融入形状先验知识。目前,已有大量相关文献报道,其中基于水平集[2],Mumford-Shah(M-S)模型[3]和先验形状[4]等具有一定的代表性。2002年,Cremers等介绍了一种将形状先验和M-S模型结合的统计模型[5],这种模型将曲线显性地表示为一条封闭的样条曲线。2003年,Tsai等提出的形状分割模型[6],基于Leventon的形状模型[7]和Chan和Vese提出的M-S简化模型,即C-V模型[8]。该隐性形状先验利用一个位置矢量和一个形状矢量实现先验形状的变化。位置矢量用于空间变换,形状矢量则是通过将符号距离函数隐性表示的形状训练集进行主元分析(principal component analysis,PCA)得到且用于表示形状差异的变化。2006年,Bresson等采用了和Tsai一样的隐性先验形状表示方法[9],不同之处在于,Bresson的模型在分割图像的过程中,通过形状、边界和区域三个函数来调节图像信息和形状先验知识在不同分割场合中的作用力度。
上述模型采用的先验形状模型或是固定的,或是可变的。不过即使是可变的,也只能在平均先验形状基础上通过特征矢量的线性组合实现一些简单的变化,变化范围不大。因此,感兴趣物体的形状不能和先验形状相差太大。这是由于他们提取训练集特征的方法采用的是PCA。众所周知,PCA是一种线性方法,只利用了先验知识的二阶统计信息。当待分割物体的形状过于复杂或者有非线性形变的时候,往往得不到满意的分割结果。Cremers等2004年首先成功地将核方法通过Parzen估计应用于几何主动轮廓(geometric active contour,GAC)模型,从而构建了形状信息在核空间的分布模型[10]。Dambreville等2008年运用核主元分析(kernel PCA,KPCA)方法捕捉形状信息,建立了形状模型,并将其嵌入GAC分割模型中,成功地分割出正踢球的足球员和鲨鱼等[11]。不同于PCA,KPCA能提取出数据的非线性特征,以及高阶统计信息等更多的信息,应用该模型能分割出形状复杂的、或有非线性变形的目标物体。
本研究提出了一种新的基于KPCA和形状先验知识的图像分割模型。该模型中,分割曲线(含形状训练集)由水平集隐式表示,利用KPCA提取训练集的非线性特征以扩大分割范围;同时,将提取出的形状先验知识引入基于区域的可变形模型,运算效率高而且鲁棒性强。这样,能够根据不同质量的图像,调节先验知识和图像信息两者的作用力度,从而得到最佳的分割结果。
1 原理回顾
1.1 用水平集表示形状
采用Leventon等2000年提出的隐式形状表示法[7],该方法是基于Osher和Sethian提出的水平集方法[2]。一个形状/闭合曲线C通过一个更高维的符号距离函数φ隐式表示,φ是一种特殊的水平集函数,定义为
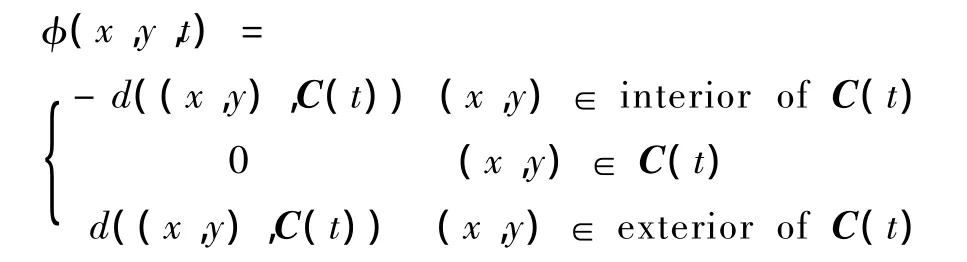
式中,d表示点(x,y)到曲线C的最短欧式距离,t是表示曲线进化过程中的时间步长。训练集中的形状/曲线表示为高维函数φ的零水平截集,即C(t)={(x,y)|φ(x,y,t)=0}。水平集表示法有很多优点,如能精确地表示形状,算法稳定,易于实现曲线的分裂、合并、形成尖角等拓扑变化等。
1.2 KPCA
KPCA可以认为是线性PCA的推广,是一种提取数据非线性特征的强有力法[12]。KPCA的基本思想很简单,首先将输入空间RN的数据X通过一个非线性变换φ映射到更高维的特征空间F,然后再在空间F中对这些投影数据进行主元分析(PCA)。一般来说,变换函数φ是非线性的,将本在输入空间里不能线性分类的数据经过映射变换后,在特征空间实现线性分类,如图1所示。
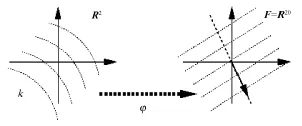
图1 线形空间RN到非线性空间F的映射[12]Fig.1 Projection from linearspaceRNto nonlinear oneF[12]
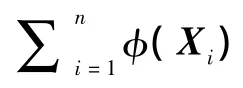
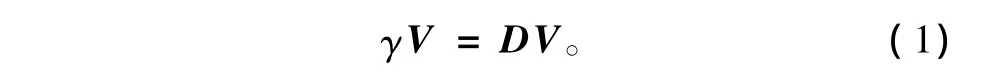
由于V属于φ(X1),φ(X2),…,φ(Xl)的生成空间,因此有
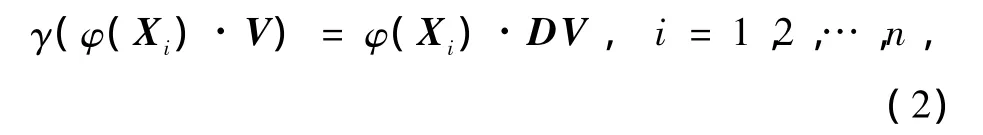
并且存在参数αi,使得V可由φ(Xi)线性表出,即V=。定义一个n×n的矩阵K:Kij=k(Xi,Xj)=(φ(Xi)·φ(Xj)),将D、V的表达式代入式(2)中,于是可得式(1)的等价式为:nγα=Kα,α=(α1,α2,…,αn)T。因此求出K的特征值和特征向量,即求得式(1)的解。这样就可提取出测试点X在映射空间的非线性主元,其第l主元为
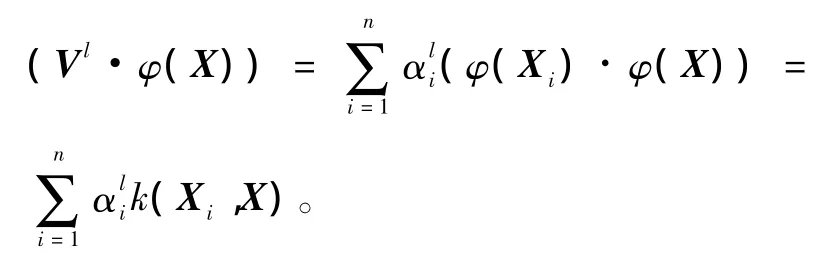
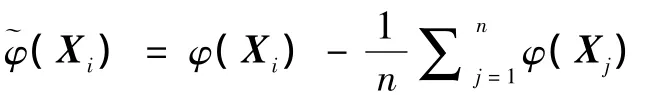
2 基于KPCA的可变形模型
笔者所提出的是基于KPCA的可变形模型,该模型基于Chan和Zhu[13]提出的先验形状分割模型。设图像矩阵I的领域范围为Ω,距离函数φ表示进化曲线,ψ为训练集平均形状的符号距离函数。源形状φ和靶形状ψ之间的关系用距离简单地表示。在Chan-Vese(C-V)分割模型[8]和Paragios等[14]的形状模型的基础上,Chan-Zhu(C-Z)给出了其能量方程[13]
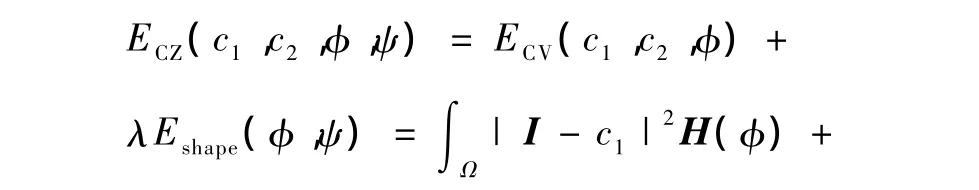
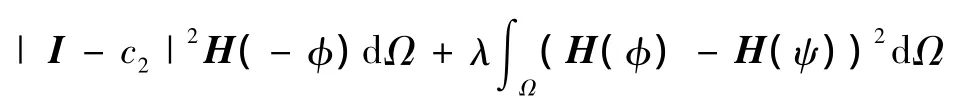
式中,H是Heviside函数,c1和c2分别为曲线C内部和外部的图像I的平均灰度值,λ≥0是图像信息(第一项)和形状先验(第二项)的权重。形状先验项引导曲线φ逼近形状先验ψ,因此该模型能分割出部分遮挡的物体。
但是,先验ψ是一个固定的形状,为输入空间的训练集的平均形状,它仅仅吸引着曲线逼近平均形状,这表明目标物体的几何形状应和先验形状的几何形状相接近。换言之,这是C-Z模型某种意义上的缺点,它没有充分利用训练集里所包含的所有个体的差异先验信息,而仅仅利用了他们的共有先验信息——平均形状,这极大地限制了该模型的分割范围以及分割效果。
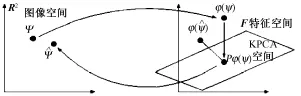
图2 KPCA的逆映射Fig.2 The preimage problem of KPCA
采用的核函数为高斯核k(Xi,Xj)=exp(-‖Xi-Xj‖2/(2σ2)),那么图像空间的距离函数=Eshape就可以用特征空间的距离函数来表示:
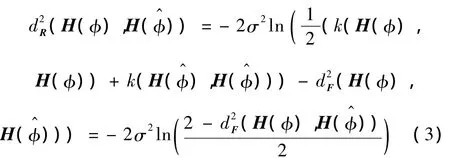
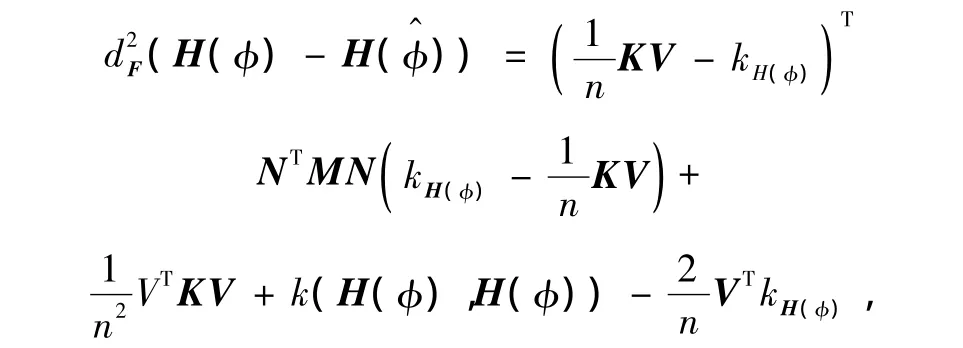
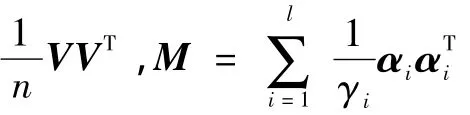
因此,基于KPCA的先验形状分割模型的能量方程为
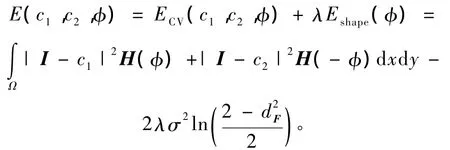
然后运用欧拉方程和变分方法,对φ进行最小化E,可以得到曲线进化方程
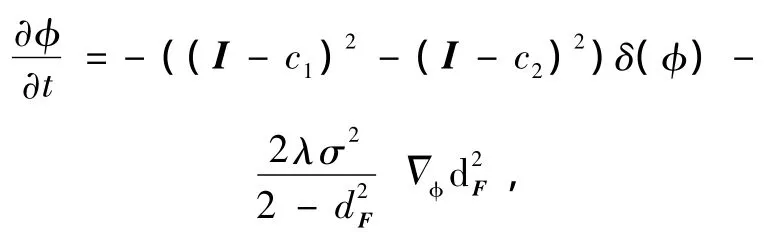
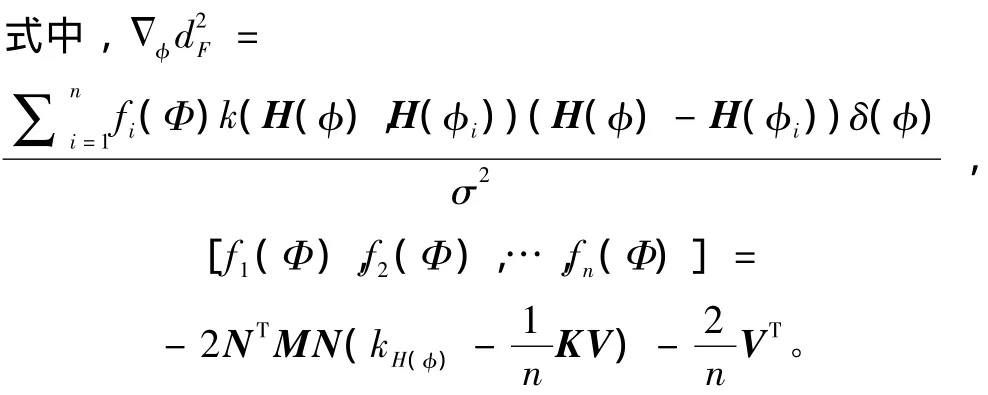
参数λ和σ的选取关系到图像分割质量的高低。λ用于调节图像信息和先验信息在分割过程中分别所占的比重,σ的大小影响着所获得的曲线形状和先验形状的差异程度。因此选取时,要综合考虑图像的质量和物体的几何形状。当图像质量不好时(比如物体部分被遮挡或者有残缺,或者噪声太大,或者有其他灰度值接近的物体和感兴趣物体相连),应该由先验信息来正确引导曲线的进化。因此应增大λ的值以加强先验项的比重。同时应该减小σ,将曲线的形状严格的限制在一定的形变范围内,减少其他因素的影响。反过来,当感兴趣目标的几何形状和先验形状相差较大时,要得到合适的有意义的进化曲线,应更多的考虑给定的图像信息,而不是先验信息。因此应减小λ增强图像项的比重,同时增大σ扩大曲线的形变范围。此时曲线的进化结果更多的依赖于给定的图像信息。
3 算法验证
利用合成图像和真实图像,将笔者的模型和基于PCA的分割模型分割结果进行比较,对所提出的算法进行验证。
3.1 采用合成图像
采用文献[6]中的飞机训练集。该训练集包含12架飞机(如图3(a)所示),每幅图像大小为231像素×231像素。由于飞机的大小位置相互间存在差异,在提取形状先验前需进行配准,从而消除大小位置带来的误差。配准方法也采用文献[6]中的方法,第一架飞机固定不变,作为参考,将其余飞机进行刚性变换,与其对齐,得到图3(b)所示的配准结果。
另外,选1幅不包含于训练集的飞机图像用于测试实验,并在这幅测试图的基础上,再添加了其他的干扰因素,则生成3幅待分割图像。第1幅中的飞机被大量的高斯噪声所污染,噪声信噪比为10dB;第2幅为有残缺的飞机,其50~60行被置为背景色,并添加了10dB的高斯噪声;第3幅采用的干扰因素为3×5栅栏和10dB高斯噪声。每根条栅的宽度为7个像素,灰度值与飞机一致。竖条栅的起始横坐标依次为35、75、115、150和190;横条栅的起始纵坐标依次为40、105和180。在栅栏的干扰下,飞机被严重污染,且部分边界被模糊。
考虑到基于PCA的分割模型的初始曲线不能和分割结果相差太大,一般选用平均形状作为初始曲线。因此在下面的分割实验中所选用的初始曲线均为平均形状。
3.2 真实图像
选取36张大小为128像素×128像素的含肝CT图像,并由专家手工分割出肝,将此作为提取肝形状特征的训练集。
同样地,用于分割测试的肝图像不包含于训练集,初始曲线为平均形状。
4 结果
4.1 合成图像
图3中(a)和(b)分别为采用文献[6]中的飞机训练集和相应的配准结果。可以看出,经过配准后,图(b)中的飞机的大小和位置基本一致,机头均朝正上方。

图3 含有12架飞机的训练集。(a)配准前;(b)配准后Fig.3 Training data of 12 binary airplanes.(a)before alignment;(b)after alignment
图4~图6分别为人工合成噪声污染图像、残缺图像和栅栏污染图像及其分割结果。各图中,(a)为包含初始曲线的测试图,(b)和(c)为初始曲线分别在PCA分割模型和本模型驱使下演变的最后结果。总体而言,本模型在3幅图像上得到的结果均好于基于PCA分割模型的结果。尽管基于PCA分割模型几乎检测出了整个飞机,但是仍有部分曲线和飞机的实际边界有一定的距离,如飞机头,两侧的翅膀和机尾。特别是图6中分割出的翅尖不但包含真实的边界,还包含与其相连的背景栅栏。而本模型则给出了令人满意的结果,特别是图4,通过调节图像信息项和先验信息项在分割中的比重,使得曲线最终吸引到正确的物体边界。即使是存在强干扰的图5和图6,本模型也给出了不错的结果,检测出了想要的飞机形状。这得归功于KPCA,一方面KPCA将分割曲线限定在先验形状周围,排除外界的干扰,另一方面又允许分割曲线发生较大的或非线性的形变,更贴近飞机真实的边界。

图4 噪声污染图像的分割结果。(a)初始曲线;(b)PCA分割模型;(c)本模型(λ=0.9,σ=1)Fig.4 Segmentation of the noised airplane.(a)initialization;(b)result using PCA;(c)result using our model

图5 残缺图像的分割结果。(a)初始曲线;(b)PCA分割模型;(c)本模型(λ=0.8,σ=3)Fig.5 Segmentation of the incomplete airplane.(a)initialization;(b)result using PCA;(c)result using our model
4.2 真实图像
与合成图像同理,需在提取形状先验前将36幅肝CT图像训练集进行配准。因篇幅原因,图7仅列出了其中的15幅,如图7所示。其中,(a)为配准前的图像集,(b)为配准结果,图中肝的大小、位置和朝向几乎一致。

图6 栅栏污染图像的分割结果。(a)初始曲线;(b)PCA分割模型;(c)本模型(λ=0.8,σ=3)Fig.6 Segmentation of the grilled airplane.(a)initialization;(b)result using PCA;(c)result using our model
图8所示为CT肝图像的分割结果。可以看出,PCA分割模型分割出了肝的整体形状,不过在某些肝的细节上却差强人意,如右上角的尖角和中下方的凹处都没有得到很好的分割。相比较而言,本模型在分割肝的过程中,一方面KPCA允许进化曲线的形变范围扩大,另一方面肝的灰度信息和边界信息正确地引导进化曲线逼近正确的肝的边界,因此最终在这两处都得到了准确的分割结果。

图7 含有15个肝的训练集。(a)配准前;(b)配准后Fig.7 Training data of 15 binary livers.(a)before alignment;(b)after alignment
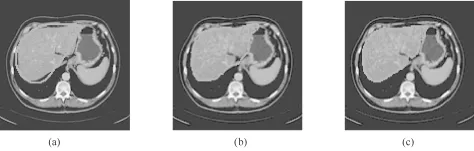
图8 CT肝图像的分割结果。(a)初始曲线;(b)PCA分割模型;(c)本模型(λ=0.8,σ=1)Fig.8 Segmentation of the liver.(a)initialization;(b)result using PCA;(c)result using our model
5 讨论
由于成像过程中存在各种噪声污染、电磁等影响,医学图像质量不高,普遍存在边缘模糊、残缺、不同组织之间的界线不清晰等问题。而且呼吸运动和个体差异也导致欲分割的器官存在一定的形变和差异。此时仅利用图像信息的可形变模型很难得到理想的分割结果。如图9(c)所示,仅利用图像信息的C-V模型尽管分割出了肝,但也分割出了和肝灰度值近似的其他器官如胃、脾等。
对此,笔者所提出的模型融入了用KPCA分析的形状先验知识,利用KPCA代替PCA能提出更有价值的先验形状的特征向量,扩大了分割范围,使得分割模型不但可以正确处理一般的污染严重、有遮挡和信息缺失的情况;而且,即使待分割形状与先验形状有着非线性的形变,也可以得到正确分割。在KPCA分析得到的形状模型引导下,分割质量不好、存在个体差异、却有着丰富训练集的医学图像,也能得到满意的分割结果。在图8的分割结果中,尽管平均形状的右下方没有凹处,但KPCA允许进化曲线发生较大的形变,因此最终的结果出现了本研究想要的凹处,而PCA则没有出现。不过KPCA的该性能也使得右上角分割出了和肝紧连的部分胃壁,这和本研究采用的C-V模型有关,该模型所采用的分割特征为灰度值,因此灰度值接近的胃壁也被分割出来了。在分割过程中,虽然可以调节σ和λ来得到不同的分割结果,但想得到很满意的分割结果,参数的调节并不容易。

图9 CT肝图像的分割结果。(a)原始图像;(b)专家分割结果;(c)C-V模型Fig.9 Segmentation of the liver.(a)original image;(b)result by expert;(c)result using C-V model
再则,该模型选取了任意的一个逆映射函数,而不是固定的平均形状,作为参考形状。该逆映射函数是分割进化曲线在KPCA特征子空间的映射,它随着曲线的进化而发生着变化,最终的进化曲线可以和训练集中任意一个个体近似,充分利用了训练集里所包含的所有个体的差异先验信息。这给初始曲线的选择预留了足够的空间,不仅仅局限于平均形状。图10中,利用手工绘制的多边形作为初始曲线,尽管该曲线和最终曲线的形状相差较大,但由于进化过程中该初始曲线不断地逼近训练集中的个体,因此得到的最终结果还是令人满意的。
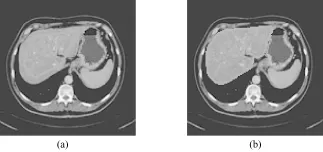
图10 选用其他初始曲线的分割结果。(a)初始曲线;(b)分割结果(λ=0.7,σ=2)Fig.10 Result using another initialization.(a)initialization;(b)result
6 结论
仅利用图像信息的可形变模型对于质量不高的医学图像来说很难得到理想的分割结果。融合先验知识和图像信息是提高分割质量的一条有效途径。本研究提出了一种新的基于形状先验知识和KPCA的图像分割模型,并将该模型应用于医学CT图像。该模型利用KPCA提取先验知识,构建形状模型,并将其融入基于区域的C-V模型。在比较实验中,所提出的分割模型应用于合成图像和医学CT图像,取得了满意的结果。与基于PCA的模型所得的分割结果相比较,该模型更能准确地识别待分割物体,尤其当图像质量较差(背景污染严重、缺损、含错误信息等)和待分割物体的形状与先验形状差别较大(非线性形变等)时具有显著优势。
本研究所提出的分割模型在进行KPCA分析时,采用了经典的高斯核函数,其他核函数(如多项式核函数)在应用于图像分割中的性能表现还值得进一步研究。此外,本研究的目标是将此模型进一步扩展应用到3D医学图像,使其自动分割更具准确性和鲁棒性。
[1]Kass M,Witkin A,Terzopoulos D.Snakes:Active contour models[J].International Journal of Computer Vision,1988,1(4):321-331.
[2]Osher S,Sethian J.Fronts propagating with curvature dependent speed:algorithms based on the hamilton-jacobi[J].Journal of Computational Physics,1988,79(1):12-49.
[3]Mumford D,Shah J.Optimal approximations by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics,1989,42(5):577-685.
[4]Chen Y,Thiruvenkadam S,Huang F,etal.On the incorporation of shape priors into geometric active contours[C]//Proceedings of the IEEE Workshop on Variational and Level Set Methods.Washington:IEEE,2001:145-152.
[5]Cremers D,Tischhauser F,Weickert J,et al.Diffusion snakes:Introducing statistical shape knowledge into the mumford-shah functional[J].International Journal of Computer Vision,2002,50(3):295-313.
[6]Tsai A,Yezzi A,Wells,W,et al.A shape-based approach to the segmentation of medical imagery using level sets[J].IEEE transactions on medical imaging,2003,22(2):137-154.
[7]Leventon M,Grimson W,Faugeras O.Statistical shape influence in geodesic active contours[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.South Carolina:IEEE,2000:316-323.
[8]Chan T,Vese L.Active contours without edges[J].IEEE Transactions on Image Processing.2001,10(2):266-277.
[9]Bresson X,Vandergheynst P,Thiran J.A variational model for object segmentation using boundary information and shape prior driven by the mumford-shah functional[J].International Journal of Computer Vision,2006,68(2):145-162.
[10]Cremers D,Osher S,Soatto S.Kernel density estimation and intrinsic alignment for knowledge-driven segmentation:teaching level sets to walk[C]//Proceedings of Springer Pattern Recognition.Rasmussen:Springer,2004:36-44.
[11]Dambreville S,Rathi Y,Tannenbaum A.A framework for image segmentation using shape models and Kernel space shape priors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2008,30(8):1385-99.
[12]Schölkopf B,Smola A,Müller K.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation,1998,10(5):1299-1319.
[13]Chan T,Zhu W.Level set based shape prior segmentation[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington,DC:IEEE,2005:1164-1170.
[14]ParagiosN,Rousson M,Ramesh V.Matching distance functions:A shape-to-area variational approach for global-tolocal registration[C]//Proceedings of Computer Vision.Copenhagen:Springer,2002:813-815.
[15]Kwok J,Tsang I.The pre-image problem in kernel methods[J].IEEE Trans Neural Netw,2004,15(6):1517-1525.
