采用阈值修正法改善电阻抗图像质量

陈晓艳 张 静

（天津科技大学电子信息与自动化学院，天津 300222）

引言

电阻抗断层成像技术（electrical impedance tomography，EIT）是近30年发展起来的新兴检测技术［1］，其基本原理是利用物场内介质的阻抗（电阻或电导）特性，通过施加驱动电流（电压）来测量响应电压（电流），重建物场内部的电阻率分布及其变化的图像［2］。图像重建算法是电阻抗图像重建的核心技术，其实质是利用场域内多组边界电压、电流的关系，计算场域内部电阻率的分布或变化。但是，由于EIT技术的“软场”病态特性，致使其图像质量不尽如人意，所以，如何提高电阻抗图像的重建质量，是国内外专家关注的热点问题［3-4］。

目前，提高电阻抗图像重建质量的手段有两种：一种是图像重建算法研究［5-6］，另一种是图像的后处理方法研究。通过对重构图像进行再加工，增强图像显示力，提高分辨率。

本研究提出采用阈值修正法对EIT图像进行图像后处理，利用高斯牛顿算法和等位线滤波反投影算法对场域内多个目标的分布情况进行图像重建，利用相对误差和相关系数对修正前后的图像进行评价，验证了该方法有效可行，最后对实际物场中的4种不同分布情况进行图像重建和改进。

1 原理与方法

1.1 阈值修正法原理

阈值修正法的基本原理是：根据电导率变化范围合理选择某一阈值，根据各单元电导率与阈值的关系，按照修正公式，重新获得重构图像的各单元电导率值。阈值的选取与目标物体电导率和背景电导率密切相关。

当目标电导率大于背景电导率时，修正公式为

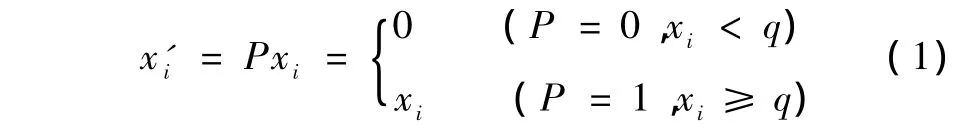
式中，修正前各单元的电导率为xi（i=1，2，…，m），修正因子为P，阈值为q，0≤q≤max（xi）。

当目标电导率小于背景电导率时，修正公式为

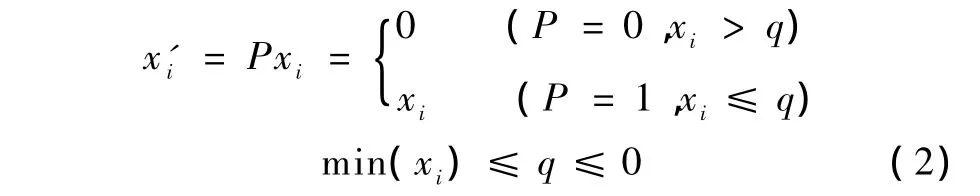
算法不同、目标不同，阈值取值也不同。阈值的选取主要由成像效果、相对误差及相关系数三因素决定。若修正后图像的相对误差减小，且相关系数提高，则该阈值选取合理。

阈值过大，会丢掉有用信息，造成图像失真；阈值过小，会保留过多信息，达不到去除伪迹、提高图像分辨率的目的。只要寻找到合理阈值，去除冗余，保留有效信息，就会改善重建图像的质量。

1.2 重建算法

选用高斯牛顿算法和等位线滤波反投影算法进行图像重建，其算法原理简述如下。

1.2.1 高斯牛顿算法

高斯牛顿算法（Guass-Newton algorithm，GN）是基于Newton法的迭代法，对于零向量问题至少有二阶收敛速度［7-8］，所以当设定的初始电导率足够接近于真实电导率分布时，迭代次数会大大减小，成像效果明显增强。目标函数为

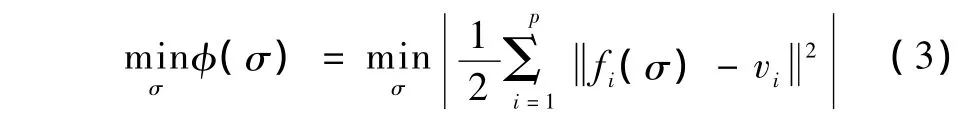
式中，fi（σ）为正问题中预设电导率计算出的边界电势分布，vi为实际物体表面所测的电势分布。对应的Gauss-Newton问题为求解

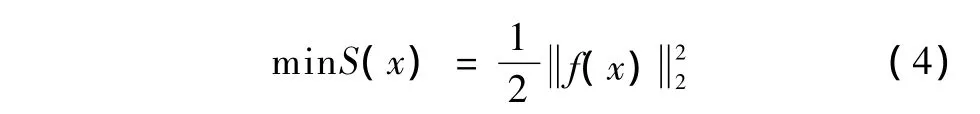
采用的高斯牛顿算法是：通过预迭代，选取足够接近于真实电导率分布的初始电导率，然后经过一步迭代，得到场域电阻率分布的近似解，从而完成图像重建。

1.2.2 等位线滤波反投影算法

等位线滤波反投影算法（equi-potential filter back-projection algorithm，EFBP）是目前应用最为广泛的EIT图像重建算法［9-10］，是借鉴X射线计算机断层成像反投影技术的一种动态电阻抗成像算法。X-CT技术中的反投影是沿直线（射线）方向进行反投影，等位线反投影算法是将测量的边界电压标准化后沿等位线方向进行反投影，而EFBP算法则是对边界电压数据滤波和标准化后再沿等位线方向进行反投影。

EFBP算法的矩阵表达为

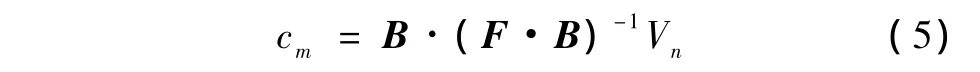
式中，（F·B）-1为滤波矩阵，B为反投影矩阵，矩阵F描述了标准化的边界电压变化与标准化的电导率变化间的标准化灵敏度关系，Vn是经标准化处理的边界电压变化。

EFBP算法可减少图像伪迹，提高图像分辨率，成像效果优于直接反投影算法。

1.3 评价指标

为了对比修正前后的图像性能指标，采用相对误差和相关系数进行量化评价。

1.3.1 图像相对误差

图像相对误差用于衡量重建图像与原始图像间的误差，表达式为

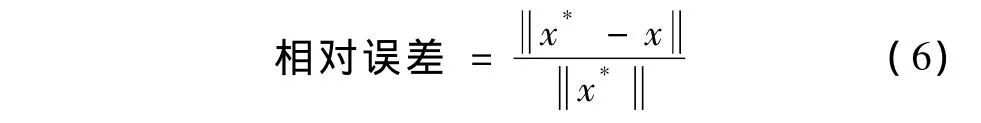
式中，x*表示原始图像归一化灰度矢量，x表示重建图像归一化灰度矢量。

图像相对误差越大，重建图像质量越低。

1.3.2 图像相关系数

图像相关系数用于判断重建图像与原始图像的相关程度，能够有效地衡量重建图像的质量，其表达式为

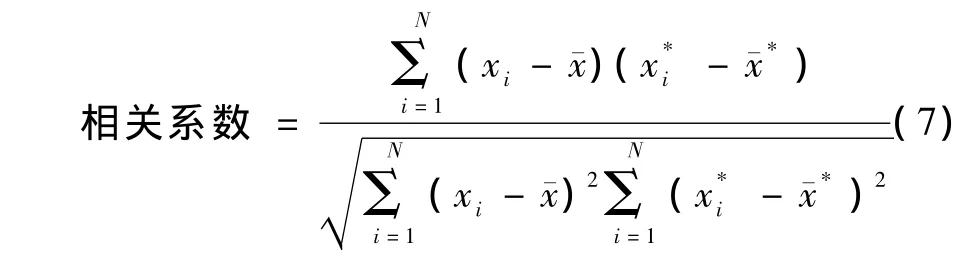
式中，x*为原始图像归一化灰度矢量，x为重建图像归一化灰度矢量*为原始值的平均值，为重建值的平均值。

图像相关系数越大，相关性越强，重建图像质量越高。

图1 仿真图像重建结果。（a）不同目标数的原图像；（b）修正前GN；（c）修正后GN；（d）修正前EFBP；（e）修正后EFBPFig.1 Simulation reconstructed images.（a）original images with different targets；（b）previous images by GN；（c）post images by GN；（d）previous images by EFBP；（e）post images by EFBP

2 结果

2.1 仿真结果及分析

在Matlab软件环境下，建立圆形场域，设置目标电导率为0.5、背景电导率为1。分别采用高斯牛顿算法和等位线滤波反投影算法，对1～7个目标物体的分布进行图像重建，结果见图1中（b）列和（d）列。其中，高斯牛顿算法中的修正阈值选取q=-0.14，等位线滤波反投影算法选取q=-0.16，修正后的重建结果见图1中（c）列和（e）列。可以看出，修正后图像的伪影明显减少，分辨率有所提高。

按式（6），分别计算两种算法修正前后的相对误差（relative error，RE），结果如表1及图2～图3所示。按式（7），分别计算两种算法修正前后的相关系数（correlation coefficient，CC），结果如表2及图4图5所示。

由表1～表2和图2～图5可知：q=-0.14对于高斯牛顿算法而言，具有较好的改善效果，图像相对误差最多可以减小55.12％，图像相关系数最多可以提高49.34％；q=-0.16对于等位线滤波反投影算法而言，图像相对误差最多可以减小97.39％，图像相关系数最多可以提高105.7％，改善效果比较理想。

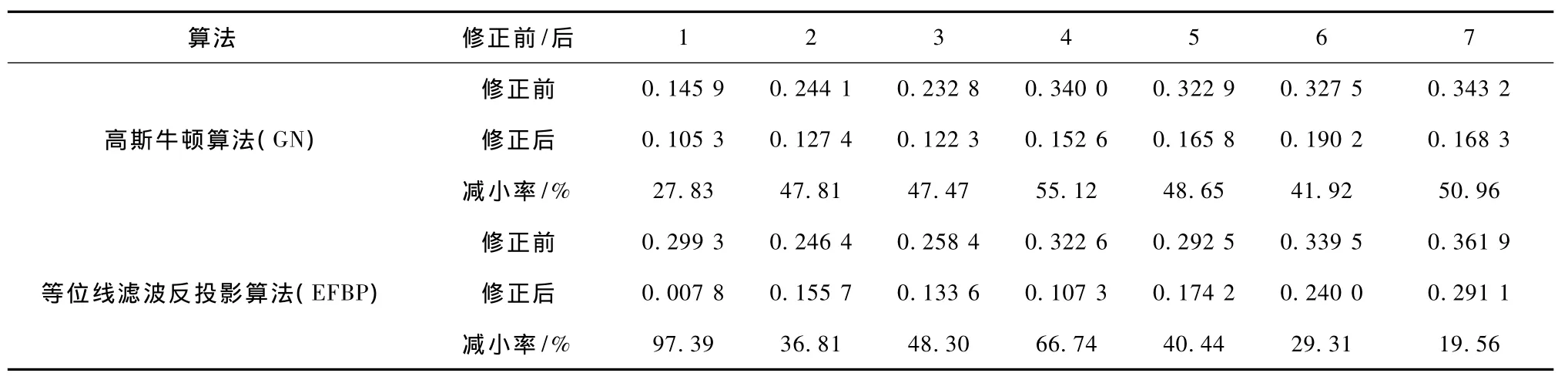
表1 相对误差Tab.1 Relative errors

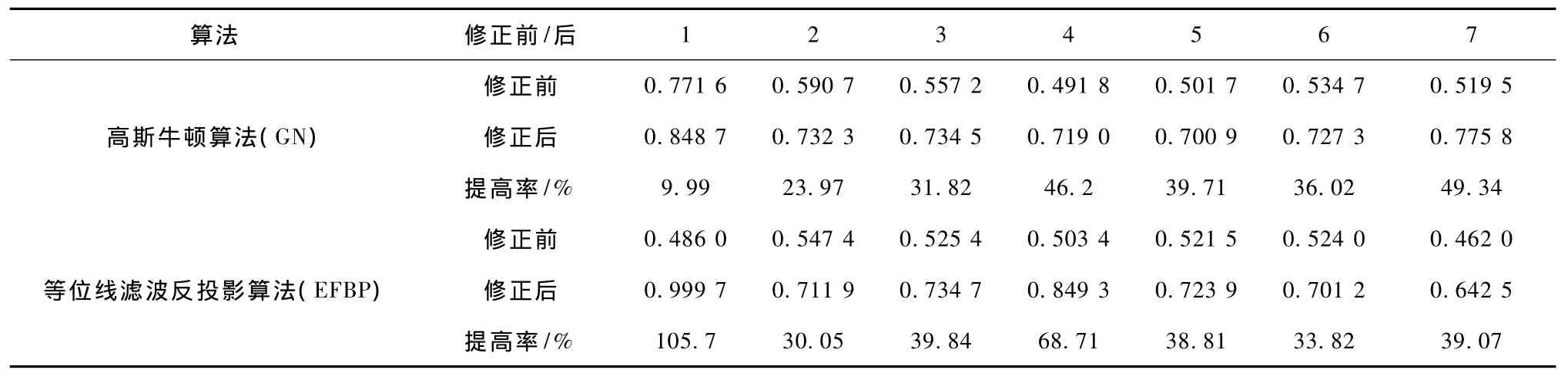
表2 相关系数Tab.2 Correlation coefficients

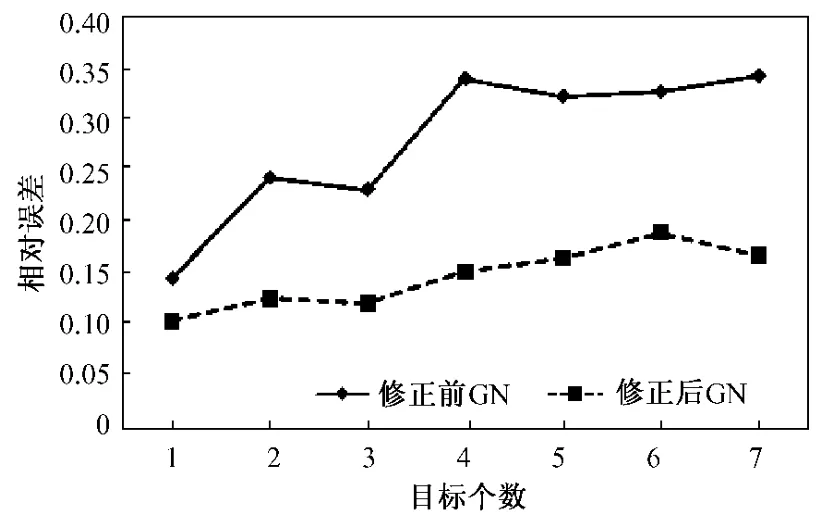
图2 基于GN算法的相对误差曲线Fig.2 Comparative RE of previous and post images by GN

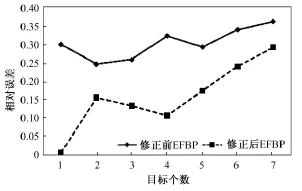
图3 基于EFBP算法的相对误差曲线Fig.3 Comparative RE of previous and post images by EFBP

2.2 实验结果及分析

实验装置采用16电极均匀分布的圆形盐水槽，内径28cm，背景溶液电导率为0.012 5S/m，目标物体为有机玻璃棒，其电导率远小于溶液电导率。电阻抗成像系统采用电流激励电压测量/相邻激励相邻测量的工作模式。重建算法采用高斯牛顿算法成像，算法中的各参数与仿真时采用的参数完全一致。重建及修正后的效果如图6所示，可以看出修正后图像的伪影明显减少，分辨率有所提高。

相对误差和相关系数计算结果如表3及图7～图8所示。从中能够看出，修正后的图像相对误差最多可以减小52.85％，相关系数最多可以提高13.2％，图像分辨率有所提高，成像伪迹有所减少，图像质量得到了改善。

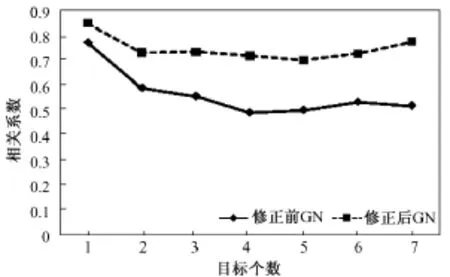
图4 基于GN算法的相关系数曲线Fig.4 CC curves of the previous and post images by GN

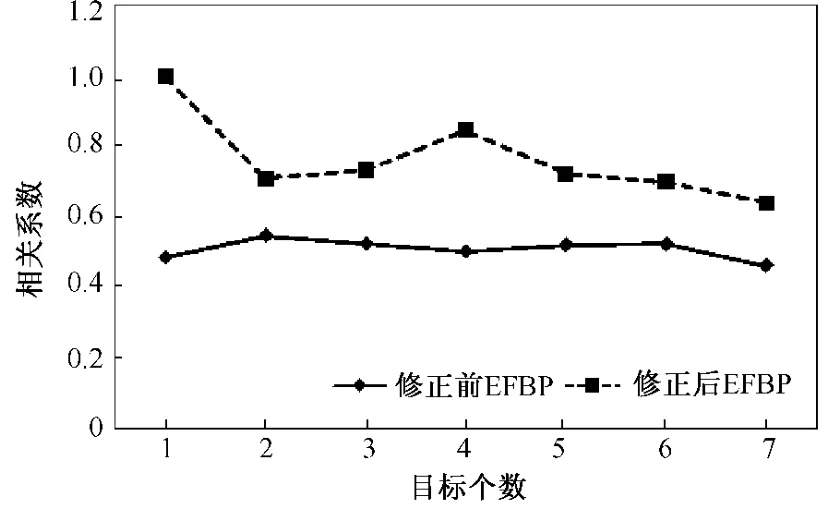
图5 基于EFBP算法的相关系数曲线Fig.5 CC curves of the previous and post images by EFBP

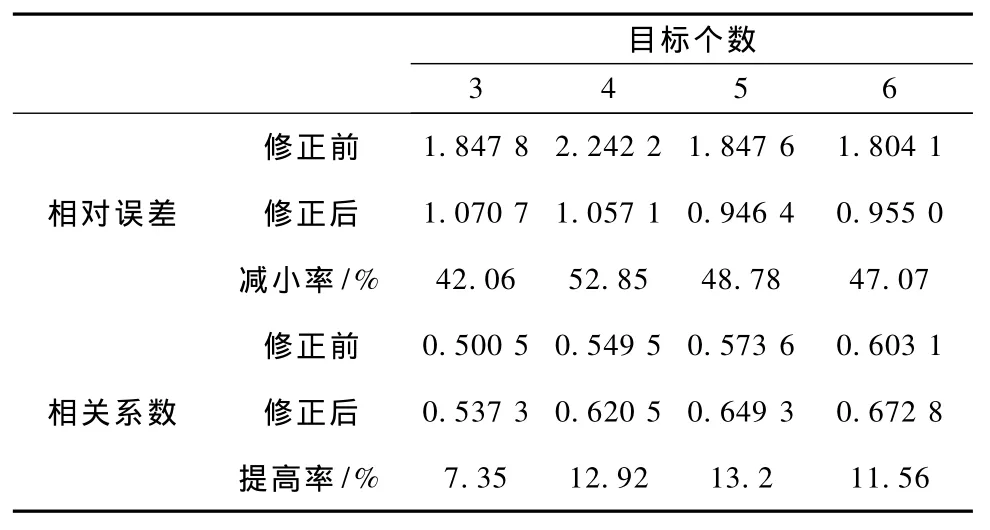
表3 GN算法修正前后的相对误差和相关系数Tab.3 RE and CC of the previous and post images by GN

3 讨论和结论

本研究提出阈值修正法，它是对逆问题的解进行修正的一种简单而有效的图像后处理方法。该方法仅对目标电导率小于背景电导率的情况进行了探索性的研究与验证，但为更好地将电阻抗成像技术与生物医学应用相结合，还将对目标电导率大于背景电导率及两种电导率条件同时存在的情况进行拓展研究。此外，采用阈值修正法改善电阻抗图像质量的方法虽然简单、有效，但如果通过建立优化函数或计算优化指标来选取阈值，则将会取得更好的改善效果。

图6 实验图像重建结果。（a）不同目标数的实验图像；（b）修正前GN；（c）修正后GNFig.6 Reconstruction images based on tests.（a）experimental images with different targets；（b）previous images by GN；（c）post images by GN

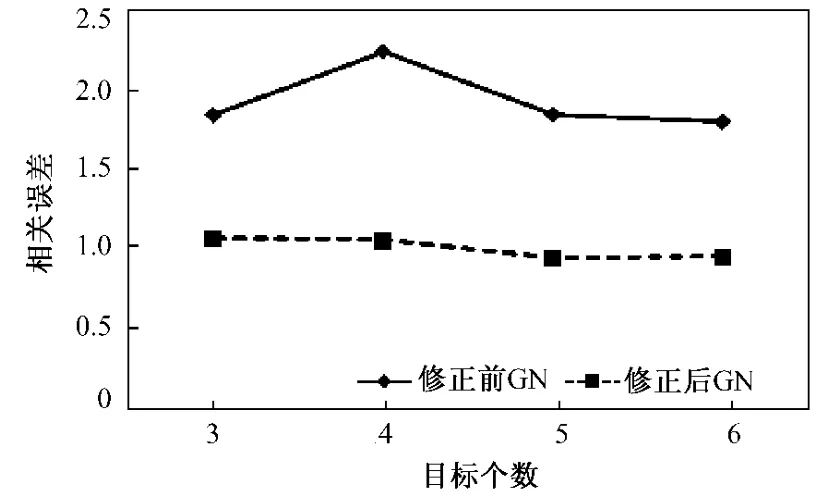
图7 修正前后的相对误差曲线Fig.7 Relative errors of the comparative images

为了提高电阻抗图像重建质量，本研究提出了阈值修正法，并采用高斯牛顿算法和等位线滤波反投影算法进行图像重建，利用相对误差和相关系数两项指标分别对修正前后的重建结果进行了评价。仿真和实测结果表明，修正后图像的分辨率显著提高，伪影明显减少，而且相对误差和相关系数的两项性能指标得到提高。本研究提出的方法有效可行，有利于EIT技术在工业及生物医学工程领域发挥更大的优势。

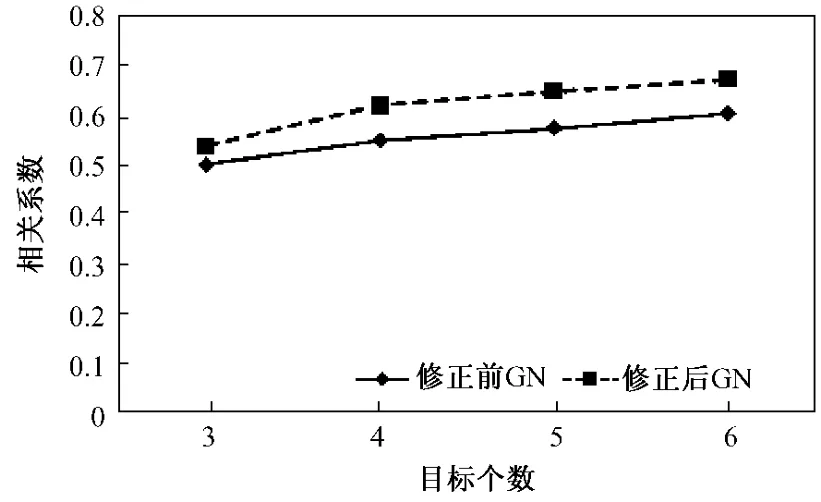
图8 修正前后的相关系数曲线Fig.8 Correlation coefficients of the comparative images

［1］任超世，王妍，邓娟.电阻抗断层成像应用技术研究［J］.中国医疗器械杂志，2007，31（4）：235-238.

［2］董秀珍.生物电阻抗成像研究的现状与挑战［J］.中国生物医学工程学报，2008，27（5）：641-643.

［3］邓娟，王妍，吕婧华，等.三种EIT算法重建图像评价的仿真研究［J］.医疗卫生装备，2010，31（5）：1-4.

［4］帅万钧，董秀珍，付峰，等.一种电阻抗断层成像重建数据的可视化方法［J］.第四军医大学学报，2008，29（6）：522-525.

［5］王化祥，范文茹，胡理.基于GMRES和Tikhonov正则化的生物电阻抗图像重建算法［J］.生物医学工程学杂志，2009，26（4）：701-705.

［6］黄嵩，张占龙，罗辞勇，等.电阻抗静态成像中混合正则化算法抗噪性能的仿真研究［J］.中国生物医学工程学报，2009，28（2）：309-313.

［7］陈晓艳，王化祥，石小累，等.人体肺功能生物电阻抗成像技术［J］.中国生物医学工程学报，2008，27（5）：663-668.

［8］谭冬莲，肖汝诚.基于改进Gauss-Newton法的在役桥梁结构参数识别［J］.长安大学学报（自然科学版），2007，27（4）：57-60.

［9］罗辞勇，朱清友.改进的电阻抗反投影成像算法［J］.重庆大学学报，2009，32（3）：243-246.

［10］吴梦秋，程正兴.反投影重建算法的改进算法［J］.西安工业学院学报，2004，24（1）：76-81.

［11］Lionheart W，Polydorides N，Borsic A.The reconstruction problem［M］//Holder DS.Electrical Impedance Tomography Methods：History and Applications.Bristol：Inst Phys Pub，2005：1-65.

［12］Tanguay LF，Gagnon H，Guardo R.Comparison of applied and induced current electrical impedance tomography［J］，IEEE Trans Biomed Eng，2007，54（9）：1643-1649.

［13］Manuchehr S，Catherine P，Nick P.Improving the forward solver for the complete electrode model in EIT using Algeberic multigrid［J］.IEEE Trans Medical Imaging，2005，24：577-583.

［14］Kauppinen P，Hyttinen J，Malmivuo J.Sensitivity distribution simulations of impedance tomography electrode combinations［J］.International Journal of Bioelectromagnetism，2005，7（1）：344-347.

［15］SoleimaniM，Gomez-Laberge C，AdlerA.Imaging of conductivity changes and electrode movement in EIT［J］.Physiol Meas，2006，27：103-113.

［16］彭黎辉，陆耿，杨五强.电容成像图象重建算法原理及评价［J］.清华大学学报，2004，41（4）：478-484.