舰载导弹发射数值模拟与点火时机研究①

2011-08-31陈余军赵刚练

固体火箭技术 2011年6期

陈余军，姜毅，赵刚练

(北京理工大学宇航学院，北京 100081)

0 引言

在舰船上发射导弹，受海情的影响舰船姿态具有动态随机性，任意时刻和状态下的发射得到的导弹出筒姿态几乎都不相同，根据制导与控制系统对导弹出筒姿态参数的要求［1］，需要对各种环境和条件下的发射出筒姿态进行预估，为制导控制系统的设计提供参考，对武器系统的设计与评估有重要意义。随着舰载武器的发展，国内外学者已在相关技术领域展开了相关研究，齐强等［2］基于理论力学方法建立运动方程组分析海情变化对导弹初始弹道的影响;于存贵等［3］基于Adams软件分析了舰载火箭炮在不同海况下的射击精度;段齐骏等［4］运用船舶耐波性理论，并结合概率与数理统计原理研究了舰载武器装备发射精度与载体运动的关系。目前研究多数基于理论力学方法讨论载体运动及海况对武器发射精度的影响，对于武器发射极限状态及时机选择的研究几乎空白。

本文围绕舰载导弹发射问题，重点分析舰载发射的恶劣状态以及导弹出筒姿态与海况、推力、发射点及发射时刻之间的关系。考虑到计算工况纵多，文中将利用成熟而高效的商业软件Adams平台，通过模型参数化和脚本语言实现舰载导弹发射过程的自动化仿真和数值试验，找出最恶劣的发射状态和较合理的发射条件和窗口，为弹上控制系统设计和发射控制提供综合性参考。

1 动力学仿真建模

1.1 模型简化

考虑到导弹发动机点火失败引起的发射安全性问题［5］，舰载导弹武器系统通常采用准垂直方式(通常向侧舷倾斜小于5°)发射。本文选取垂直自推力不同时离轨的舰载发射系统为设计对象，依据多体动力学原理对舰载导弹发射系统进行简化，简化后的系统由导弹、前后滑块、导轨、发射筒和舰船等构件组成。舰载发射系统简化模型示意如图1所示，其中A、B分别代表靠近船头和船尾的2个发射点。

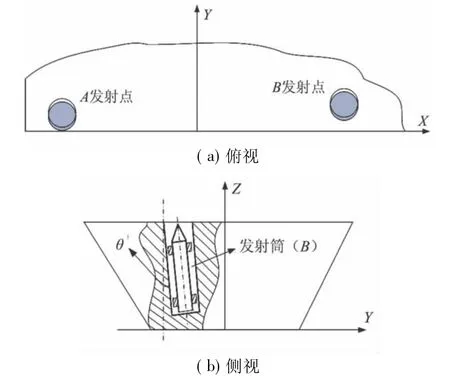
图1 舰载发射系统示意图Fig.1 Diagram of ship-based launch system

1.2 动力学模型

点火前导弹随舰船一起在海浪中摇荡，点火后导弹瞬间沿导轨运动，初始阶段前后滑块都受到约束，接着前后滑块先后相继滑离导轨。导弹运动经历了全约束到半约束的过渡，由于载体的摇荡运动以及滑块与导轨之间的间隙因素，整个导弹发射过程的运动和受力十分复杂。

为建立动力学模型进行假设如下:

(1)所有构件均假设为刚体，不考虑结构变形对导弹运动的影响;

(2)除滑块与导轨之间的非理想约束，其他连接均假设为理想约束;

(3)实际中导弹与船舰质量相差悬殊，并考虑到后文船舰运动描述方便，忽略发射时导弹运动对舰船运动产生的影响;

(4)为考虑更恶劣情况，为船舰初置一个横摇和纵摇角度。

各构件之间连接关系:滑块与导弹固连;导轨与发射筒固连;发射筒与舰船固连;滑块与导轨之间为接触约束。基于Adams建立多体动力学模型，作用在弹上推力由发动机点火试验数据拟合得到，可选取不同的推进剂组分得到不同大小的推力。

为描述导弹运动，定义弹体坐标系Om-xmymzm，原点位于导弹质心，x沿弹轴并指向弹头，z沿舰船横摇轴方向，y根据右手坐标法则确定。记弹体角速度在弹体坐标系Om-xmymzm下沿三坐标轴方向的分量为滚转、偏航和俯仰角速度，对应角位移则由积分得到。

1.3 动力学方程与求解

Adams采用拉格朗日乘子法建立系统动力学方程:

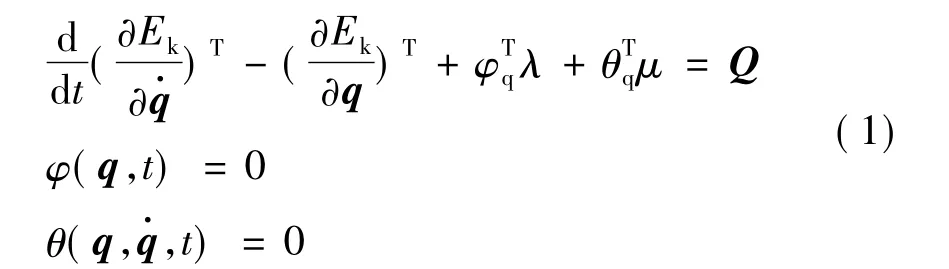
式中 Ek为系统动能;q为系统广义坐标列阵;Q为广义力列阵;λ为对应于完整约束的拉氏乘子列阵;μ为对应于非完整约束的拉氏乘子列阵。

采用GSTIFF积分器通过Gear预估校正算法可求解上述矩阵方程。

1.4 接触参数设置

舰船的摇摆使得导弹上的滑块与导轨发生接触碰撞，从而直接影响导弹的运动规律和出筒姿态，且舰船位于不同姿态时滑块与导轨的接触碰撞情况也不一样。选择合理的间隙接触计算模型和进行准确的参数设置是保证仿真精度的重要因素，本文采用非线性弹簧阻尼模型模拟含间隙的接触碰撞问题，相应的接触碰撞力计算公式［6］为

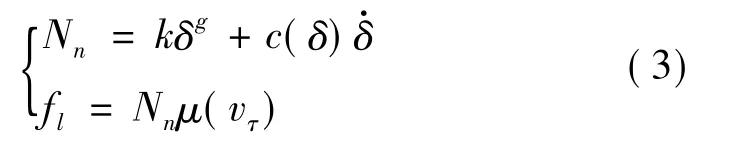
式中 Nn为两物体间的法向作用力;ƒl为两物之间的切向作用力即摩擦力;k为等效刚度系数;c(δ)为阻尼函数;δ为两物体沿法线方向的最大穿透量;μ(vτ)为摩擦系数函数;vτ为切向相对运动速度。

滑块和导轨的材料分别为钢和铝，参考软件帮助设置参数:接触刚度为38 000 N/mm，碰撞阻尼系数为28 N·s/mm，弹性力贡献指数为1.5，最大穿透深度为0.1 mm，静摩擦系数为0.3，动摩擦系数为0.1，静摩擦转换速度为0.1 mm/s，动摩擦转换速度为10 mm/s。

2 舰船运动模拟

舰船的运动特性与海况、自身结构和航向有关。实际舰船在海中的运动十分复杂，为研究方便需要进行简化，本文重点考虑舰船的横摇、纵摇和垂荡运动对导弹运动及出筒姿态的影响。

实际的舰船运动由多个不规则波下分运动的线性叠加组成，由于缺乏舰船的具体属性参数，无法通过船舶耐波性原理和切片理论求解舰船在海中运动响应参数。

容易知道，越恶劣海况下导弹发射越危险，本文采用有限赋值法思想，选取摇荡幅值及对应最小周期构成的正弦波来描述舰船运动，这样能够代表某级海况的极限工况，分析极限状态下导弹的出筒姿态可作为设计的临界条件，因此舰船的垂荡、横摇和纵摇运动可简化描述为［7］

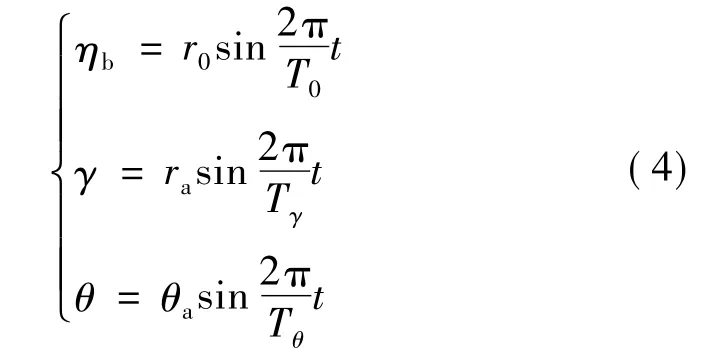
式中 ηb、γ、θ分别为垂荡位移、横摇位移和纵摇位移;r0、T0分别为垂荡幅值和周期;ra、Tγ为横摇幅值和周期;θa、Tθ为纵摇幅值和周期。

本文研究的舰载武器系统属于大型舰船，其在4、5级海况下的摇荡特性参数如表1所示［8］。

表1 大型舰船的摇荡幅值与周期Table 1 Straying amplitude and cycle of big ship

定义与大地固连的地面全局坐标系O-xyz，原点位于舰船重心;与舰船相连的舰船坐标系Os-xsyszs，原点位于舰船重心。在上述坐标系下，通过Adams中的Point Motion工具定义舰船的6自由度运动，并根据式(4)定义舰船的横摇、纵摇和垂荡运动函数。容易看出，舰船的姿态与时间有关，不同时刻点火舰船位于不同姿态。

3 数值仿真试验设计

根据表1中舰船的横摇、纵摇和垂荡各分运动的周期，选取最小周期描述舰船运动，在不考虑各分量初始相位情况下由最小公倍数原理得到舰船运动近似周期为40 s。为模拟舰船不同姿态下的点火，对舰船一个运动周期进行离散且每隔0.5 s进行采样发射，对应点火时刻分别取 0、0.5、1、…、40 s，计算每 1 次发射导弹的出筒姿态，得到舰船姿态与其对应的导弹出筒姿态之间的变化规律，单个周期内单发弹的试验总次数为81。

为考察A、B两发射点在2种不同推力、2种不同海况下的发射特性，共需要进行发射试验总数为81×8=648种。推力分别取为TL1和TL2，且TL1＜TL2，海况取4级和5级。

由于试验工况和结果数据文件较多，本文通过自编程序循环调用Adams软件的批处理命令进行动力学仿真，具体步骤为:通过程序修改模型cmd文件得到不同工况需要的模型及参数设置，在后台通过批处理命令调用和运行cmd文件，仿真得到相应的结果数据文件，最后通过自编程序进行数据处理得到不同点火时刻导弹出筒角位移和角速度。虚拟试验的整个计算流程如图2所示。

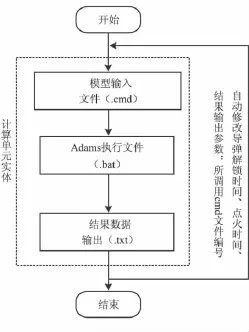
图2 虚拟试验流程Fig.2 Virtual experiment process

4 仿真试验结果

通常使用角位移和角速度描述导弹运动，前者描述姿态的初始偏差，后者反映速度变化的快慢，文中选取角速度参数进行描述。

4.1 不同推力下的发射模拟

进行了5级海况下A、B发射点在TL1和TL2推力下的发射试验，得到导弹出筒角速度随点火时刻的变化如图3所示。

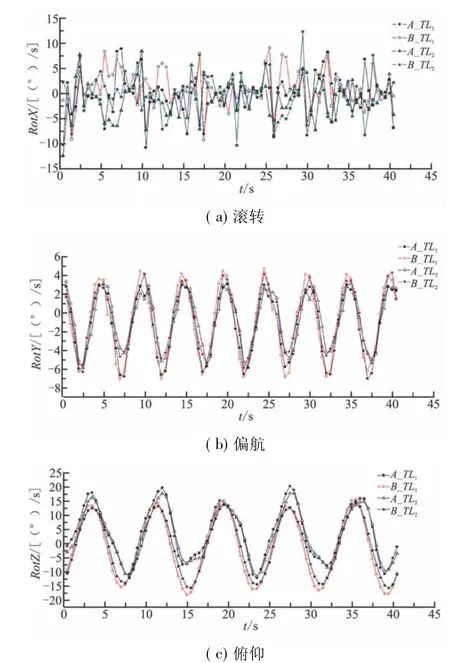
图3 导弹出筒角速度随点火时刻的变化曲线Fig.3 Change curves of missile outlet angular velocity with ignition time

由图3(a)可知，滚转角速度曲线无明显周期特征。相同推力下，不同发射点对应最恶劣工况的点火时刻不一致，且A发射点曲线峰值较B发射点的大;同一发射点，不同推力下对应最恶劣工况的点火时刻不一致，曲线峰值与推力呈反比。滚转姿态主要受滑块和导轨之间的接触碰撞影响，与离轨时刻碰撞情况直接相关;不同发射点受船舰牵连运动影响形成的碰撞程度不一致;小推力发射下导弹在轨运动时间长，与导轨接触碰撞次数多，受牵连运动影响可能性增加。

由图3(b)可知，偏航角速度曲线有8个波峰，曲线波动平均周期约为5 s，与舰船纵摇运动周期接近;各曲线波峰波谷对应时刻较为一致。相同推力下，B发射点曲线峰值稍大于A发射点;同一发射点，峰值与推力呈反比关系;曲线的非零对称特性与模型中舰船的初始相位相匹配。出筒偏航姿态主要由船舰纵摇分运动的牵连运动形成，偏航姿态变化与船舰纵摇分运动规律相一致，两者在该分量上的相对运动基本可忽略，各曲线之间的差异与发射点距离纵摇轴位置相关。

由图3(c)可知，俯仰角速度曲线有5个波峰，曲线波动平均周期约为8 s，与舰船横摇运动周期接近;各曲线峰值对应时刻基本接近。相同推力下，A发射点峰值稍大于B发射点;同一发射点，曲线峰值与推力呈反比;俯仰曲线非零对称性同样与船舰放置的初始位置相关。与偏航姿态相对应，俯仰姿态主要由船舰横摇分运动的牵连运动产生，同样该分量上的相对运动基本可忽略，各曲线之间差异还与发射点距离横摇轴位置相关。

4.2 不同海况下的发射模拟

为研究海况对导弹发射出筒姿态参数的影响，对舰船在4、5级海况下的发射进行数值试验，其中推力取TL1，得到出筒角速度峰值如表2所示。

表2 TL1下导弹出筒角速度峰值Table 2 Outlet angular velocity peak of missile under thrust TL1

由表2可知，4级海况下导弹出筒姿态角速度各分量峰值相对5级海况均有所下降，尤其是俯仰和偏航姿态，几乎为线性变化关系，因为舰船的横摇、纵摇峰值大小直接影响导弹的出筒偏航和俯仰姿态;不同海况下，相同推力及发射点对应的姿态曲线在不同时刻达到峰值。

为验证仿真结果，取5级海况对应的6发弹试验数据，其中推力TL1下A点发射对应的导弹出筒俯仰角速度最大值为22.6(°)/s、偏航角速度最大值为10.7(°)/s，滚转角速度最大值为 12.4(°)/s，与表 2数值仿真试验结果相比各参数在量级上基本吻合，相应的误差则由于实际海况的复杂性难以真实模拟以及仿真模型简化等因素形成。综合对比情况反映出仿真模拟结果基本满足工程精度要求，表明文中建立的数值仿真模型基本可信，可用于工程计算与分析。

5 点火时机分析

根据上述模拟结果得到，导弹出筒姿态与发射点位置、推力、海况以及发射时的舰船姿态均相关，需要根据具体发射状态确定点火时刻。仍然选取代表导弹飞行特性的角速度参数作为点火可行的判断指标，为考虑各姿态分量的综合效应，进行角速度求模，得到导弹出筒角速度的模

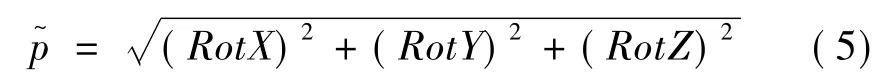
其中，右边3项分别对应出筒时刻的俯仰、偏航和滚转角速度分量。

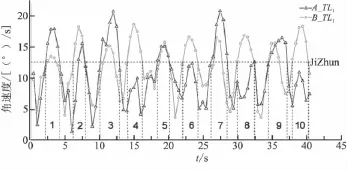
图4 导弹出筒角速度模随点火时刻的变化曲线Fig.4 Change curves of missile outlet angular velocity modular with ignition time

图4反映出2条曲线波峰对应时刻基本一致，曲线的波峰和波谷基本相互交替包含，A发射点p～曲线峰值较B发射点的高。根据相应战术指标要求，定义导弹出筒姿态角速度模低于12.5(°)/s对应的时间区间为安全点火区间，超出部分对应的时间区间定义为危险区间。由图4曲线得到A、B发射点的公共危险点火时刻区间有 1、2、3、5、7、9，仅属于 B 发射点危险点火时刻区间有4、6、8、10，那么在选取的发射周期内除去上述区间即为安全点火区间。

依据上述定义得到，A发射点的安全点火区间近似为(单位:s):［0，2］、［4.2，6.1］、［7.9，10］、［12.8，17.2］、［20，26.1］、［28.4，34.4］、［37，40］。B 发射点的安全点火区间近似为(单位:s):［0，2］、［4.2，6.1］、［7.9，10］、［12.8，14］、［16.1，18.3］、［20.1，22］、［24.2，26.1］、［28.4，29.8］、［32.4，34.4］、［37，38］。将这些数据载入发射控制程序，在导弹点火前瞬间实时判断当前时刻是否在有效点火区间内，实现通过选取点火时机提高发射精度。

此外，考虑到不同分量恶劣工况对应的时刻不一致性，有必要结合制导控制系统对出筒姿态各个分量的敏感性和调控能力来确定主姿态分量，在此基础上对上述安全点火区间进行修正，得到满足要求的点火区间。