未确知测度综合评价模型在长江水质评价中的应用

李 恩，薄立磊

(河北工程大学经济管理学院，河北邯郸056038)

由于长江流域干流以及比较大的支流受到了严重污染，威胁着人类生存的环境，因而对长江水资源的保护和治理迫在眉睫.水质评价方法目前主要有灰色聚类法、模糊综合评价法等.每个评价方法各有特点，但是在实际应用中会经常遇到一些问题［1］.笔者利用信息熵确定指标区分权重，同时建立未确知测度综合评价模型.利用此方法可以更直观地表述长江目前的水质状况，更准确地确定影响长江水质的主要污染物成分，为保护长江水资源奠定良好的基础.

1 水质的未确知测度评价模型

在未确知测度评价模型中将评价对象空间记为X，即 X= { x1，x2，…，xn}，对于评价空间X需要对m个指标进行测量，从而将指标空间记为I，即指标空间为 I= {I1，I2，…，Im}，将第i个对象xi关于第j个指标 Ij的测量值记为 xij，则评价空间为 U={c1，c2，…，cp}，对象xi关于指标的测量值可表示为一个 m 维向量 xi= (xi1，xi2，…，xim)，i=1，2，…，n.若评价等级ck比 ck+1强，记为 ck＞ck+1.若 c1＜c2＜…＜cp或 c1＞c2＞ … ＞cp，则称评价空间{c1，c2，…，cp}为评价空间U的一个有序分割类［2］.

1.1 单指标未确知测度

设 μijk=μ ( xij∈ck)表示测量值xij属于等级ck的程度，如果μ满足

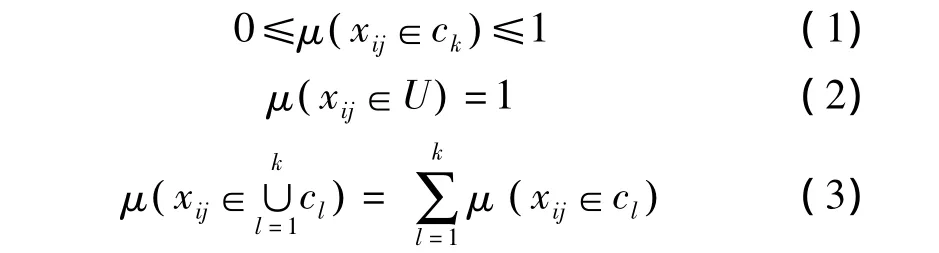
则称 μ( xij∈ck)为未确知测度.称 ( μij1，μij2，…，μijp)为xi的单指标未确知测度向量，称矩阵

为单指标测度矩阵［3］.其中:i=1，2，…，n;j=1，2，…，m;k=1，2，…，p.

1.2 基于信息熵的指标区分权重

熵概念最早起源于热力学，由克劳修斯提出，用于描述系统的状态.后来，申农将熵运用于信息论中，为了将信息和不确定性关联起来，引入概率论作为度量信息的数学工具，从而可应用于更多领域.

当属性值xij及评价指标给定后，属性权重已相应确定，隐藏在属性测值的未确知测度中，所以一般不宜再人为规定，应根据属性实测值来确定各个权重.借用信息熵的概念来定义指标Ij的权重［4］，

式中:k为评价级别数目vij的大小反映指标Ij的重要性程度.定义指标Ij的权重为

1.3 多指标综合未确知矩阵

设 μik= μ ( xi∈ck)表示对象xi属于等级ck的程度，令

为多指标综合测度评价矩阵.

1.4 识别准则

则可以判定xi属于第ki个评价等级cki.

可以知道xi的综合得分，可按qxi的大小来对xi进行排序.

2 长江水质的实例研究

在长江上设置7个观测站点分别为:四川攀枝花(x1)、湖北宜昌南津关(x2)、江西九江河西水厂(x3)、安徽安庆皖河口(x4)、江苏南京林山(x5)、四川泸州沱江二桥(x6)、江西九江蛤蟆石(x7).以溶解氧(DO)、高锰酸盐指数(CODMn)、氨氮(NH3－N)3项指标作为影响长江水质的指数［5］.前提假定:①污染源全部位于江段的观测点上;②污水及污染物一旦排入河流后，能够迅速分散开，并处于均匀分布状态;③长江水流是单向流动，并且流量稳定.根据2003年6月到2005年9月28个月的水质监测数据建立数学模型.

2.1 评价因素的选择

根据对长江28个月水质监测和《地表水环境质量标准》(GB3838—2002)中3个主要项目标准限值，设评价指标I1为溶解氧、I2为高锰酸盐指数、I3为氨氮，地面水环境标准见表1.

表1 地面水环境标准

从表1得知，指标I1的指标类型成降序分布，指标I2和I3的指标类型均成升序分布.

2.2 单指标未确知测度函数

指标I1，I2，I3的不确知测度函数均采用折线型，如图1—3所示.表2给出了各监测点的监测数据.

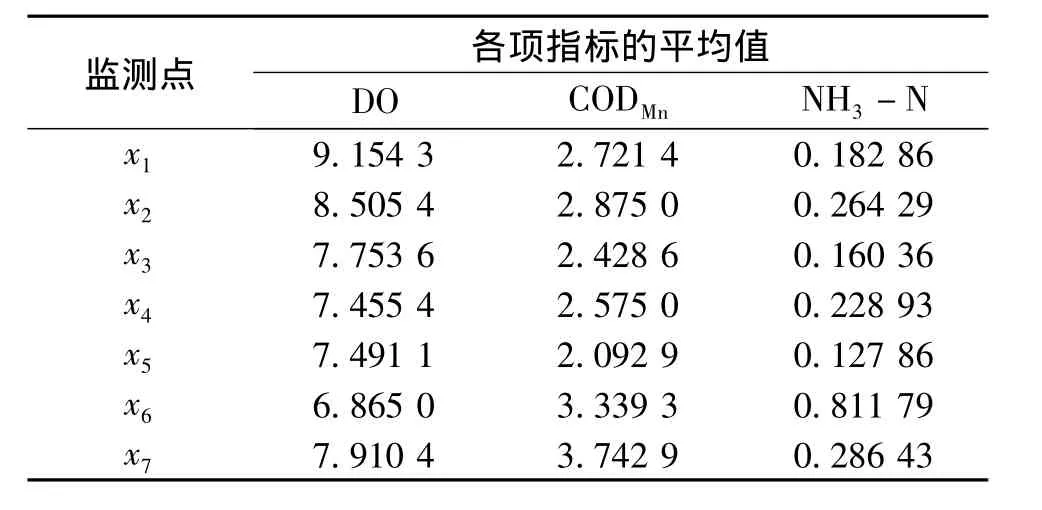
表2 各监测点监测数据

由表2的监测值及单指标测度函数图1—3，可得样本的单指标测度评价矩阵.如

2.3 多指标综合测度评价矩阵

由公式(6)及单指标测度评价矩阵得样本x1的指标分类权重向量为

由单指标测度评价矩阵及指标权重向量按公式(7)得样本x1的综合测度评价向量为

同理可求得多指标综合测度评价矩阵为

2.4 识别与评分排序

取置信度λ=0.6，由综合测度评价矩阵(11)可判别xi的污染等级见表3.

表3 样本污染等级

3 结语

采用未确知测度评价模型对长江7个观测站点2003年6月至2005年9月的水质进行了综合评价.评价结果表明:四川攀枝花为Ⅱ级水质，湖北宜昌南津关为Ⅱ级水质，江西九江河西水厂为Ⅱ级水质，安徽安庆皖河口为Ⅱ级水质，江苏南京林山为Ⅱ级水质，四川泸州沱江二桥为Ⅳ级水质，江西九江蛤蟆石为Ⅱ级水质.此结论与国家环保局按月公布的该时间段长江流域水质监测报告结果基本一致.

运用该模型，选取溶解氧、高锰酸盐和氨氮3项指标作为未确知测度模型的判别指标，使得评价体系全面而且简洁，利用信息熵理论计算各影响因素的指标权重减少了人为主观因素的影响，依照置信度识别准则进行等级判定，从而为水质评价提供了一条新的途径.

［1］庞彦军，王小胜，栗文国.基于指标区分权重的未确知测度综合评价模型及其应用［J］.大学数学，2008，24(1):120－124.

［2］刘开第，庞彦军，张博文.水环境质量评价的未确知测度模型［J］.环境工程，2000，18(2):58 －60.

［3］庞彦军，刘开第，姚立根.滏阳河水质综合评价［J］.运筹与管理，2001，10(1):82 －88.

［4］郭章林，刘兆鹏.基于信息熵的未确知测度模型在煤矿安全评价中的应用［J］.煤矿安全，2010(9):138－140.

［5］肖明杰.改进的模糊综合评价模型在水质评价中的应用［J］.水科学与工程技术，2007(4):6－9.