基于灰色神经网络模型的径流模拟与应用

2011-08-28孙晗含

华北水利水电大学学报(自然科学版) 2011年6期

邱林，周茂，孙晗含

(华北水利水电学院，河南郑州450011)

准确预测流域的年径流量及分布特性，对合理开发利用水资源至关重要.灰色预测模型［1－3］所需样本数据少，无须考虑其分布规律及变化趋势，建模简单，运算方便，适用于处理数据较少、趋势性强、波动不大的短期预测问题.神经网络预测模型［4－5］具有较强的自学习、自组织和自适应能力，以及良好的非线性信息处理能力，适用于预测无序、波动较大的时间序列，在处理长期预测问题中有较大优势.为充分发挥灰色预测模型和神经网络模型各自的优势，笔者综合应用这2种模型进行流域的年径流量模拟预测研究.

1 基于GM(1，N)的灰色神经网络模型

1.1 灰色关联度分析

灰色关联分析［6］的关键在于关联度的计算.邓氏关联度［7］无论是对时间序列数据、指标序列数据还是横向序列数据都适用.其计算方法如下.

设 X0={X0(1)，X0(2)，…，X0(n)}为系统特征序列，即预报对象;Xi={Xi(1)，Xi(2)，…，Xi(n)}(i=1，2，…，m)为相关因子序列.在时刻 t，Xi与 X0的相关系数为

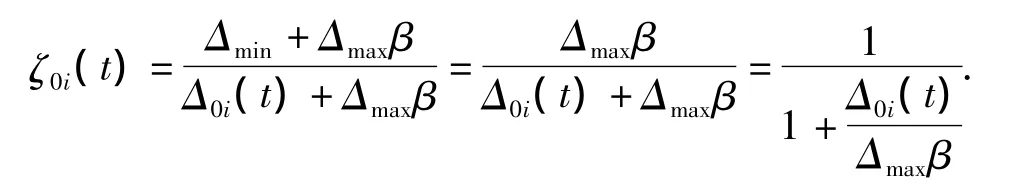
式中:Δ0i(t)为序列Xi与X0在t时刻的绝对差值;Δmax，Δmin分别为各时刻相对因子序列对系统特征序列绝对差的最大、最小值，实际计算时，需将原始数据作初值化处理，所有初值Xi(1)均变为1，故Δmin=0;β为分辨系数，通常取值0.5.由于关联性是曲线间几何形状的差别，因此选择曲线间差值的大小为衡量关联度的尺度是合理的［8］.ζ0i(t)与 Δ0i(t)/(Δmaxβ)负相关，其值不仅直接取决于 Δ0i(t)，而且间接地受系统整体性的影响.Δmax是系统整体性在关联空间中的反映，β是Δmax的系数，表示系统或各相对因子对关联度的间接影响程度.则关联度

通过灰色关联度的计算，可确定有效因子(关键因子).在灰色关联度分析中，按不同公式求得的各因子间关联度的数值大小可能会有所差异，但关联序列一般不会发生变化.因此，关联序列才是关联分析的实质［9］.

1.2 GM(1，N)模型

式中:a 为系统发展系数;bi－1(i=2，3，…，N)为驱动项;b1，b2，…，bN－1为驱动系数.^a=［a，b1，b2，…，bN－1］T为系数向量，通过最小二乘法求解得到

求解微分方程得GM(1，N)模型的时间响应函数为

累减还原式为

式(1)和式(2)即为GM(1，N)的预测模型.

1.3 模型的检验准则

设X(0)为原始序列为模拟序列，e(0)为残差序列，则X(0)的均值和方差分别为:

同理可得e(0)的均值和方差分别为:

1.4 BP神经网络修正残差

GM(1，N)模型的参数a导致预测值与原始值之间存在残差.通过BP神经网络拟合修正有效残差信息来修正GM(1，N)模型的预测值，可进一步提高预测精度.

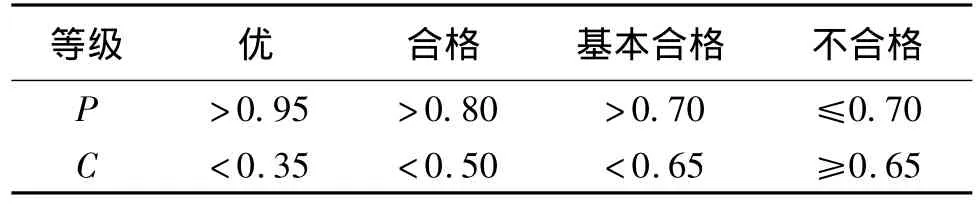
表1 精度检验等级参照表

第i时刻原始值X(0)(i)与预测值 X^(0)(i)之差，称为第i时刻的残差，记作e(0)(i)，残差序列记为e(0)={e(0)(1)，e(0)(2)，…，e(0)(n)}.若预测维数为s，则用 e(0)(i－s)，…，e(0)(i－2)，e(0)(i－1)来预测第i时刻的残差，因此将 e(0)(i－s)，…，e(0)(i－2)，e(0)(i－1)作为BP网络训练的输入样本，e(0)(i)作为BP网络的输出样本，利用足够多的残差序列对BP网络进行训练，就可将训练好的BP网络的输出作为残差序列的修正值.

2 应用实例

某河流21 a径流及相关的观测资料［12］见表2.

表2 某河流实测21 a径流及相关资料

2.1 邓氏关联度确定关键因子

已知年均径流量序列(X0)为系统特征序列，年均降雨量序列(X1)、采伐面积序列(X2)、采伐量序列(X3)和年均含沙量序列(X4)为相关因子序列.

用上述邓氏关联度分析法研究各影响因子(Xi)与年均径流量(X0)的关联程度.计算可得:r01=0.999 5，r02=0.930 9，r03=0.757 8，r04=0.992 5.关联序列为:r01＞r04＞r02＞r03.故选取年均降雨量(X1)和年均含沙量(X4)作为影响年均径流量(X0)的关键因子进行建模.

建模序列为21 a(1983—2003年)所实测到的相关数据，最后3 a(2001—2003年)数据不进序列，留作预测检验用.

2.2 年均径流量GM(1，N)预测模型

经灰色关联度分析确定年均径流量序列(X0)、年均降雨量序列(X1)和年均含沙量序列(X4)为建模序列，应用灰色建模原理，计算得到模型待定参数为=［a，b1，b2］T=［1.461 8，1.647 2，－8.593 5］T，将所得到的参数代入式(1)，得到年均径流量GM(1，N)预测模型为

式中:X(0)1(1)=180.0;a=1.461 8;b1=1.642 7;b2= －8.593 5.

对年均径流量序列的预测结果见表3.从表中可以看出模型具有较高的拟合精度.根据上述计算公式可得 GM(1，N)模型的后验差比值 C=0.408 2，小误差概率P=0.857 1，合格，该模型可用于预测.

表3 模型拟合精度比较

2.3 确定BP神经网络结构

把GM(1，N)模型预测的残差序列作为输出样本来建立BP神经网络.采用3层BP网络，经测试，当输入样本取4维，隐层节点数取6，隐含层数取1时，预测精度最高.该例共21个残差组成17个训练样本.学习率取0.06，收敛率为0.001，均方差限制在0.001，训练步长为1 000，得到前后层节点之间的联结权值.

2.4 模型预测结果比较

将训练好的BP网络输出作为残差序列与GM(1，N)模型相对应的预测值相加得到最后的预测值，基于初值修正的 GM(1，1)模型［14］、单一 GM(1，N)模型和组合模型的拟合情况对比见表3.组合模型的相对误差百分率绝对值的平均值为0.820 9%，拟合精度比单一的GM(1，N)模型的5.593 9%和基于初值修正GM(1，1)模型的15.745 6%提高许多.

2.5 年均径流量预测分析

在应用预测模型GM(1，N)对年均径流量进行预测时，必须知道关键因子在预测期内的数值.因此，还需要对年均降雨量和年均含沙量2个指标进行预测.笔者采用文献［14］中基于初值修正的GM(1，1)模型进行预测，结果见表4.应用所建立的基于GM(1，N)的灰色神经网络模型得到2004年的年均径流量预测值为107.875 8 m3/s.该结果表明，2004年的年均径流量锐减，该水库应积极采取措施多蓄水为宜.

表4 2个关键因子的预测值

3 结语

基于灰色系统建立的年均径流量预测GM(1，N)模型，考虑了影响年均径流量的诸多因子.文中通过灰色关联度分析研究确定了2个关键影响因子，在此基础上建立年均径流量GM(1，N)预测模型，这样可以有效提高预测的可靠性.然后利用BP神经网络对GM(1，N)模型的残差进行修正，进一步提高预测精度.实例应用结果表明，基于GM(1，N)的灰色神经网络模型具有较高的预测精度，是一种有效的预测方法.

［1］郝永红，黄登宇，张文忠，等.山西神头泉流量的灰色预测模型研究［J］.水利学报，2004，35(2):111 －114.

［2］马志鹏，陈守伦.水库预报调度的灰色动态规划模型［J］.水力发电学报，2007，26(5):7 －9.

［3］邱林，黄鑫，李洪良，等.基于模糊GM(1，1)模型的农业水分盈亏预测［J］.水利科技与经济，2007，13(2):69－72.

［4］张晓伟，沈冰，黄领梅.基于BP神经网络的灰色自记忆径流预测模型［J］.水力发电学报，2009，28(1):68－71.

［5］邱林，宋建娜，陈晓楠，等.基于神经网络的植被需水量模型［J］.华北水利水电学院学报，2006，27(2):4－6.

［6］王瑄，李占斌，鲁克新，等.坡面水蚀动力因子与土壤剥蚀率灰色关联分析［J］.水利学报，2005，36(5):525－530.

［7］邓聚龙.灰色系统理论［M］.武汉:华中理工大学出版社，1990.

［8］郭建博.三种灰色关联度分析法比较研究［J］.科技信息(学术研究)，2008(1):4－6.

［9］岳东杰，雷伟刚，华锡生.灰关联模型GM(1，N)及其在安全监测中的应用［J］.河海大学学报，2000，28(3):34－38.

［10］汤成友，官学文，张世明.现代中长期水文预报方法及其应用［M］.北京:中国水利水电出版社，2008.

［11］李惟佳，孙涛.灰色GM(1，N)方法在股票预测中的应用［J］.价值工程，2009(11):152－154.

［12］万星，丁晶，廖杰.水库流域年均径流模型的灰色神经网络分析［J］.水力发电，2005，31(4):18 －21.