基于自适应蚁群算法的模糊聚类算法

白亚男，司应硕

(1.平顶山学院，河南 平顶山467000;2.郑州航空工业管理学院，河南郑州450046)

聚类分析作为无监督分类的一种方法是一种硬划分，模糊集合理论被引入到聚类分析领域即发展为模糊聚类分析理论.目前研究的热点是基于目标函数的模糊聚类方法，这种方法是把聚类归结为一个带有约束的非线性规划问题，通过优化求解获得数据集的模糊划分和聚类.该方法设计简单，解决问题范围广，易于实现.模糊C均值(Fuzzy C-Means，FCM)理论［1］是此类方法中最为完善，应用最为广泛的算法.而FCM算法的缺点也是显然的，由于目标函数是非凸的，而FCM算法是迭代爬山算法，很容易陷入局部最优点或者鞍点，而不能收敛到全局的最优解.此外，算法耗时大，需要先验知识来确定待聚类的类别数目和类型.FCM算法存在的这些问题使模糊聚类问题变得更加复杂.蚁群算法［2］(Ant Colony Algorithm)是人们受蚁群群体行为的启发提出的一种基于种群的模拟进化算法，由意大利学者M.Dorigo等人首先提出［3］.该模型已成功应用于求解旅行商问题、二次分配问题［4］、job-shop调度问题、NP-完全的组合最优化问题等.为了克服蚁群算法收敛慢、容易出现停滞现象、算法的运算时间长等缺点，人们提出了大量改进算法.近年来，蚁群算法应用于模糊聚类分析的算法的研究还不够深入，蚁群聚类算法由Deneubour提出，Lumer等改进了此算法并提出了LF算法，将数据随机均匀散布在二维表格中，每只蚂蚁随机选择一个数据，根据该数据在局部邻域的相似性得到的概率，决定蚂蚁对它是否拾起、移动或放下.表格内的数据经过有限次的迭代，按其相似性而聚集，最后得到聚类结果和聚类数目.算法的不足是运行效率低，当数据集的规模增加时，其效率将不断下降.另外一类研究是将蚁群算法应用于FCM的算法［5］，其思想是由将初始聚点为食物源，其余数据样本为蚂蚁，数据聚类过程即为蚂蚁寻找最近食物源的过程，再结合FCM算法不断的修改聚类中心，达到预定阈值算法停止.此算法的缺点是需要初始化聚类原型，降低了并行搜索能力.

通过把自适应蚁群算法引入到模糊聚类问题上，笔者提出了一种新的模糊聚类算法——AACA－FC算法(Adaptive Ant Colony Algorithm－Fuzzy Clustering Algorithm)基于自适应蚁群算法的模糊聚类算法.此算法在对目标函数的优化上，利用蚁群算法的并行计算、正反馈的优点，保证了算法能跳出局部最优解而收敛到全局最优解;设计改进的蚁群算法——自适应的蚁群算法用于模糊聚类有助于改善蚁群算法初期收敛速度慢和易停滞的缺点.通过仿真实验和对比实验证明，AACA－FC算法不仅可有效地解决FCM算法存在的问题，而且达到了聚类准确度高、类内紧密度高和类间分离度大的目标.

1 基本算法描述

1.1 蚁群算法

蚂蚁是群体生活的社会性昆虫，社会成员之间存在有组织的分工、相互的通讯和信息的传递［6］.蚁群有着独特信息系统，通过信息素的不同组合，触角信号和身体动作等策动其他的个体共同协作完成任务.信息素是蚂蚁在从食物源到蚁穴返回过程中，在走过的路径上分泌的一种化学物质，这些物质在路径上形成了信息素轨迹.蚂蚁在运动过程中可以感知这种物质的存在和强度，以此指导自己的运动方向，并且使蚂蚁趋向于朝着信息素强度高的方向移动.由于信息素的存在，蚂蚁能在没有可见提示下，找到从蚁穴到食物源的最短路径，而且能够随着环境的变化而变化的搜索出新的路径，产生新的选择.在蚁群算法中，人工蚂蚁被赋予了以下的特性:

1)蚂蚁在运动过程中或者完成一次循环后，在路径上释放信息素.

2)蚂蚁以一定的概率选择下一个将要访问的结点，这个概率是两个结点间存在的信息素轨迹量的函数.

3)在完成一次循环以前，蚂蚁经过的结点不可重复.

1.2 FCM 算法

问题描述:对于待聚类的M个数据，每个数据N维属性，类别个数为c，求出第i类的聚类原型矢量 pi=(pi1，pi2，…，piN)和隶属度矩阵 U=［μik］c×N其中i=1，2，…，c，k为第k个样本数据.目标函数为

式中dik为第k个样本与聚类原型pi的欧式距离.FCM算法中，对于给定的类别数c，设定迭代停止阈值ε，初始化聚类中心模式P(0)，设置迭代计算器b=0，

步骤1 计算或者更新隶属矩阵U(b)

步骤2 更新聚类中心矩阵p(b+1):

2 AACA－FC算法

2.1 算法设计思想

2.1.1 优化函数

在AACA算法当中，优化函数为一元函数，而基于目标函数的模糊聚类算法中的目标函数却是一个关于U和P的二元函数，文献［1］对多维有约束函数优化进行了研究，但是利用蚁群算法直接对多维函数进行优化比较复杂，因此把二元目标函数转换为一元目标函数，可以简化研究.通过对模糊C均值聚类算法(FCM)的研究，其目标函数

式中:μik∈［0，1］，Ai，k;dik表示第 k个样本与聚类原型pi的欧式距离，m∈［1，+∞)为加权指数，又称为平滑参数.M为待聚类的数据个数.利用拉格朗日乘数法，根据约束条件

得出

代入公式(3)，从而使得目标函数F转化为关于pi的一元函数，即

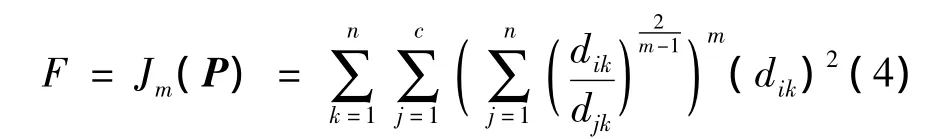
进而可将式(2)作为蚁群算法当中的目标函数进行优化.从而使得目标函数F转化为关于pi的一元函数.

2.1.2 自适应全局信息素挥发系数

当问题规模比较大时，由于信息量的挥发系数ρ的存在，使那些从未被搜索到的信息量会减小到接近于0，降低了算法的全局搜索能力.而且ρ过大时，当解的信息量增大时，以前搜索过的解被选择的可能性过大，也会影响到算法的全局搜索能力.通过减小ρ虽然可以提高算法的全局搜索能力，但又会使得算法的收敛速度降低;因此可以自适应地改变ρ的值.ρ的初始值为1，当算法求得最优解在N次循环内没有明显改进时，ρ减为

式中ρmin为ρ的最小值，可以防止ρ过小降低算法的收敛速度.

2.2 算法步骤

步骤1 为了便于在高维数据空间使用蚁群算法，采用降维方法进行处理.由于聚类原型pi=(pi1，pi2，…，piN)∈RN且 i=1，2，…，c ，因此上述 F表达式的c个N维变量可转化为cN个一维变量以此实现降维处理.问题就转化为求minF(p11，p12，…，p1N，p21，p22，…，p2N，…，pc1，pc2，…，pcN)时的 pi.便与描述算法步骤，将上式表示为求minF(p1，p2，p3，…，pcN);

步骤2 估计各个变量的取值范围，将各个变量K等分;

步骤3 给信息素矩阵τij(1≤i≤cN，1≤j≤K)各个元素赋值常数c，即τ0=c，表示所有变量的所有区间有相同的信息素量.将m只蚂蚁随机分配到初始变量p1的K个子区间内;

步骤5 设t=0;

步骤6 每只蚂蚁根据参数q0独立选择路径，到达下一个变量pi对应的某个区间j.m只蚂蚁并行工作.

式中q∈(0，1)为随机数.J为转移概率，可根据下式计算

步骤7 按下式局部更新每只蚂蚁到达的区间的信息素量τij，且取每只蚂蚁到达第i个变量对应的第j个区间的中间值为pi的当前解.

步骤8 当m只蚂蚁独立并行的选择完变量xi对应的区间后，返回步骤6，选择下一个变量对应的区间，直到m只蚂蚁都重新回到第一个变量p1所对应的区间并局部更新后，一次周游完毕.

步骤9 对于每只蚂蚁在每个区间取得的解，计算函数F的值，找到最小值对应的最优解即为本代的最优解和最佳路径.

步骤10 如果＜，则对于第 S 代的最优解按照下式进行全局更新.

步骤11 t=t+1，若t＜tmax返回步骤6，否则要找出信息素矩阵τij每行(对应于每个变量)的最大元素(信息素量最大)的列号li(对应于所分区间的编号)，利用下式缩小变量的取值范围:

其中Δ为一个正数，用于控制缩小范围的速度.t←0，转向步骤2.

步骤12 将最优解对应的解进行解码操作，转化为c×N的矩阵，即为最优聚类原型矩阵.进而可以得到隶属度矩阵.

3 AACA－FC算法仿真

实验选择一组标准数据集IRIS数据作为测试样本集，以比较算法的收敛速度和优化程度.IRIS数据由四维空间中的150个样本点组成，每一个样本具有4个分量，每个类各有50个样本.其中Setosa与其他2类间完全分类，Versicolor和Virginica之间有交叉.实验中采用的参数设置如下:m=50，qmin=0.5，ξ=0.55，ρmin=0.1，Q=100，ε =0.001，τmax=10，τmin=0.01，q0=0.01，α =1，Δ =5，

AACA－FC算法中目标函数min(F)随迭代次数的优化过程曲线如图1所示，由数据集的二维属性Sepal Length和Sepal Width绘制聚类效果图.

图1 目标函数min(F)随迭代次数的优化过程曲线

从图1可以看出，AACA－FC算法经过30代迭代收敛于全局最优解，可见自适应蚁群算法解决模糊聚类问题是有效的;通过计算，ACCA－FC算法的误分数为7，误分率为4.67%，与FCM算法10.67%的误分率相比，降低了6个百分点，进一步印证了ACCA－FC算法聚类准确率高的优点.FCM算法和ACCA－FC算法具体实验结果对比见表1.

表1 FCM算法和ACCA-FC算法实验结果对比

4 结语

提出了一种基于自适应蚁群优化算法和FCM算法相结合的新算法.一方面，把 FCM算法中的目标函数通过降维操作，将其转化为蚁群算法中的优化函数进行优化;另一方面，改进了蚁群算法，引入自适应全局信息素挥发系数，动态调节蚂蚁的路径选择和信息量的更新，不仅提高了蚂蚁的全局搜索能力，而且提高了收敛速度.仿真实验证明，新算法不仅可以有效地弥补FCM算法容易陷入局部极值点或者鞍点而得不到最优解甚至满意解的缺点，而且比FCM算法具有更好的收敛效果和更高的聚类准确率.该方法把模糊聚类问题转化为函数优化问题，为模糊聚类分析问题提供了新的解决思路.但由于蚁群算法参数的设置理论尚不完善，且实验的效果一定程度受限于参数的设置，下一步需对此进行深入探究，使算法的结果更有效.

［1］高新波.模糊聚类分析及其应用［M］.西安:西安电子科技大学出版社，2004.

［2］李士勇.蚁群算法及其应用［M］.哈尔滨:哈尔滨工业大学出版社，2004.

［3］ Dorigo M，Maniezzo V，Colorni A.Ant system:optimization by a colony of cooperating agents［J］.IEEE Transactions on SMC，1996，26(1):29 －41.

［4］ Gambardella L M，Taillard E D，Dorigo M.Ant colonies for the QAP［J］.Journal of the Operational Research Society.1999，50(2):167 －176.

［5］徐晓华，陈岐.一种自适应的蚂蚁聚类算法［J］.软件学报，2006，17(9):1884 －1889.