形状上下文在害虫识别上的应用

邱道尹，朱 云

(华北水利水电学院，河南郑州450011)

数字图像识别，是利用计算机对数字图像进行处理、分析和理解，以识别出在不同模式下的目标和对象的技术［1］.传统图像识别包括训练过程和识别过程.训练过程主要完成已知图像增强、分割及滤波、特征形成、选择及压缩、分类器设计;识别过程完成未知图像的处理，并作出识别、分类和决策.

上述方法大多采用一个特征向量来表示目标图像，而且过程复杂，因而具有一定的局限性.笔者利用一组边界点表示目标图像，即用形状上下文的方法识别害虫.

1 形状上下文

对于待识别的物体图像，通过边界检测获取图像的边界，对边界点进行采样得到了一组有限离散点集P={pii=1，2，3，…，n}，其中一点 p 到其他各点的向量相对位置简化为对数极坐标上各扇区内的点分布数，这些点的统计分布直方图Hp称为点p的形状上下文［2］.形状上下文描述的是整个轮廓形状的特征，所以不需要对图像取很多的特征值，只要求这些点尽可能地表示出物体的轮廓信息.

1.1 边界点的提取

为了描述，首先要进行分割.边界检测是图像分析中的重要内容.边界是图像的基本特征.2个具有不同灰度值的相邻区域之间总存在边界，边界是灰度值不连续的表现.常见的边界点有:阶梯形边界、屋顶形边界、线形边界.

由于边界是图像上灰度变化最剧烈的地方，传统的边界检测就是利用了这一特点，对图像各个像素点进行微分或求二阶微分来确定边界像素点.一阶微分图像的峰值处对应着图像的边界点;二阶微分图像的过零点处对应着图像的边界点.根据数字图像的特点，处理图像过程中常采用差分来代替导数运算.对于图像的简单一阶导数运算，由于具有固定的方向性，只能检测特定方向的边界，所以不具有普遍性.为了克服一阶导数的缺点，定义图像的梯度算子为

这是图像处理中最常用的一阶微分算法，式中F(j，k)表示图像的灰度值，图像梯度最重要的性质是梯度的方向在图像灰度的最大变化率上，这恰好可以反映出图像边界上的灰度变化.

对于数字图像，可用微分近似表达式表示

采用的Robert算子的表达式为

且如图1所示.

图1 Robert算法

根据上述算法，首先对害虫图像进行预处理得到二值图像，然后用Robert算子在二值图像中寻找害虫的轮廓，最后根据一定的取样间隔，得到一组有限离散点集来表示害虫的图像，如图2所示.

图2 提取害虫边界点

1.2 对数极坐标变换

极坐标系是一个二维坐标系统.极坐标系统中的点由1个夹角和1段相对于极点的距离来表示.在2点间的关系用夹角和距离很容易表示时，在平面直角坐标系中，这2点的关系就只能用三角函数来表示.所以跟平面直角坐标系相比，极坐标系具有容易表示并且便于运算处理的优点［3］.

正如所有的二维坐标系，对数极坐标系也有2个坐标轴:lnr(对数半径坐标)和θ(角坐标).传统形状上下文中极轴就是在平面直角坐标系中的x轴正方向，在此以极点到目标图像质心的方向作为极轴方向.这样，当图像在二维直角坐标系中发生旋转时，就不会改变它在对数极坐标系中的坐标.

在平面直角坐标系中的点(x，y)相对于某一点(x0，y0)，用对数极坐标来表示满足以下关系:

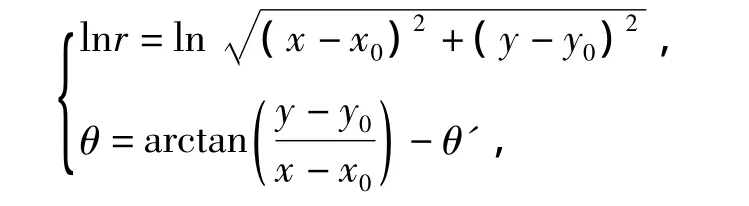
式中θ'为极点到目标图像质心的方向与x轴正方向的夹角.

当直角坐标系中的图像相对于坐标原点发生了缩放和旋转变化，如图像放大r0倍，旋转θ0角度，相应的对数极坐标变化为(lnr+lnr0，θ+θ0).所以，直角坐标系中的比例变化相对于对数极坐标系中的水平位移，旋转变化相对于对数极坐标系中的垂直位移，即对数极坐标的二维不变性.因此，当目标发生比例、旋转和平移变换后，仍能够识别出来.

1.3 形状直方图

在对数极坐标中表示了离散点之间的位置关系，对于每1个离散点，其余点和该离散点构成了n－1个向量［4］.为了更有效地表示这些向量以及他们之间的关系，笔者引入了形状直方图的概念.在计算得到某个点和剩下的个点构成的向量之后，以形状直方图的形式表示这个向量.对数极坐标系将整个空间按方向θ均分为12个方向，将距离lnr分为5份.这样，整个空间就被分成60个区域.

在点集P={pii=1，2，3，…，n}中，对于任一点p，与剩下的n－1个点构成的形状直方图的计算公式为

式中:k∈{1，2，…，60};(q－p)∈bin(k)表示对于 p点，点q属于形状直方图的第k个分量;h(k)为在形状上下文的第k个分量中所含点的个数.

图3(a)为经过采样的害虫边界点集，图3(b)和图3(d)分别为图3(a)中A点作为极点所对应的对数极坐标图和形状直方图，图3(c)和图3(e)分别为图3(a)中B点作为极点所对应的对数极坐标图和形状直方图.

图3 对数极坐标直方图

1.4 数据标准化

通过形状直方图计算的数据有不同的量纲，为了使具有不同量纲的量也能进行比较，通常需要对数据进行标准化处理.这里所说的数据标准化，就是将数据按一定的算法压缩在区间［0，1］上.

笔者采用的是极差变化法，首先进行标准差变化，即

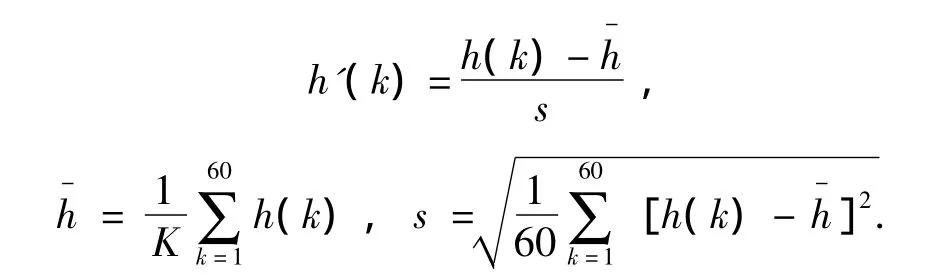
经过标准差变化后，每个变量的均值为0，标准差为1，消除了量纲的影响.但是，这样得到的h'(k)还不在区间［0，1］上.所以，还要对数据进行minmax标准化线性变化，即:

显然有0≤h″(k)≤1，符合了数据标准化要求.

1.5 相似性度量

通过标准化之后得到每个目标的形状直方图，接下来计算这两个形状直方图的相似度，从而得到两个目标的相似度并判断是否相似［4］.形状直方图之间的相似度计算方法如下.

假设有P，Q两幅待判断相似性的轮廓图像，计算P中pi点的形状直方图与Q中qj点的形状直方图之间的匹配代价，两点形状直方图的匹配代价计算公式为

式中:hi(k)为P中的pi点的形状直方图;hj(k)为Q中qj点的形状直方图.

对两幅轮廓图像中所有点的形状直方图进行一对一的匹配代价计算，即可得到两个图像的代价矩阵Cij.基于代价矩阵Cij，计算最小的总匹配代价:

式中:I为矩阵的行列数;π(i)为1个序列.计算得到的总匹配代价越小，相似度越大.

2 实验与结果分析

为了验证算法的性能，笔者使用MATLAB为软件平台来实现，采用4种害虫和其他6类图像进行比对实验，如图4所示.

实验分别对16幅图像进行两两比对，计算出最小的总匹配代价H，见表1.

图4 实验图形集

表1 图4中图形的总匹配代价值

在表1中，同一类图像的总匹配代价较小，而不同类的总匹配代价较大.最小的总匹配代价为图4(m)与图4(n)的0.07，最大的总匹配代价为图4(m)图4(o)的0.55.4种害虫图像两两之间的总匹配代价最小的为0.08，最大的为0.17.实验证明了当总匹配代价越小时，相似度越大.当总匹配代价的阈值设为0.17时，发现当总匹配代价小于0.17的图像属于同一类，总匹配代价大于0.17的图像属于不同类，这样就可以把害虫的图像从图4中识别出来.

为了验证文中改进的形状上下文算法具有对二维不变，将图4中的(a)、(b)进行比例、旋转和平移变换，如图5所示.

图5 二维变化前后对比图

当使用传统形状上下文，以x轴作为极轴方向进行相似性度量时，计算出的总匹配代价分别为0.39，0.27;当使用改进的形状上下文，把极点到目标图像质心的方向作为极轴方向时，计算出来的总匹配代价为0.05，0.07.改进的形状上下文在图像发生二维变化时，显著提高了相似性度量的准确性.

3 结语

笔者将用于描述整体轮廓特性的形状上下文引入到害虫识别中，在先对害虫图像进行预处理得到二值图像的基础上，用形状上下文描述害虫的轮廓特征.跟传统的图像识别技术相比，形状上下文不需要对图像取复杂特征值，也不需要提取图像的局部信息，只要求尽可能表示出害虫轮廓信息的边界点，就能有效地识别出害虫.当图像发生二维变化时，改进的形状上下文算法也能准确地识别出害虫图像，在前有基础上提高了识别的准确度.

［1］ Serge Belongie，Jitendra Malik，Jan Puzicha.Shape matching and object recognition using shape contexts［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002(24):509 －522.

［2］陈实，马天骏，黄万红，等.基于形状上下文描述子的步态识别［J］.模式识别与人工智能，2007，20(6):794－799.

［3］ Mori G，Belongie S，Malik J.Efficient shape matching using shape contexts［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(11):1832 －1837.

［4］申家振，张艳宁，刘涛.基于形状上下文的形状匹配［J］.微电子学与计算机，2005，22(4):144 －146.