基于载波相频差异矩阵的单通道盲分离算法

张 纯,杨俊安,叶 丰

(1.电子工程学院,安徽合肥 230037;2.安徽省电子制约技术重点实验室,安徽合肥 230037)

0 引言

目前,很多盲分离算法都假设观测信号的数目不少于源信号的数目。然而在实际应用中,由于观测条件有限,有可能会发生源信号数目多于观测信号数目的欠定情况。国内外针对欠定条件下盲分离算法的研究主要是集中在稀疏性很强的信号,即语音信号中,如利用聚类方法估计混合矩阵和最短路径法估计源信号的两阶段盲分离算法[1]、基于时频变换的欠定盲分离算法[2],上述算法在估计混合矩阵和恢复源信号时,都要求源信号满足理想的稀疏性条件。当源信号的稀疏性并不是很好时,可以通过短时傅里叶变换[3]、小波包变换[4]等方法将源信号变换到变换域上进行盲分离。但是很多信号在变换域上并不严格满足稀疏特性,此时通过上述算法并不能精确地估计出混合矩阵和分离源信号。并且上述算法并不适用于雷达信号和通信信号,对于雷达信号和通信信号的欠定盲分离算法十分罕见。

单通道盲分离作为盲源分离领域一种极端特殊的情况,是一项非常具有挑战性的工作。由于其方程数少于未知数个数的病态特点,单通道盲分离问题一直没能得到很好地解决。在该领域,目前较典型的算法有基于信号稀疏性的分离方法[5]、基于维纳滤波的分离方法[6]、基于粒子滤波的方法[7]等。这几类方法存在的最主要缺陷是算法适应性较差、分离不完全、残余成分较大。针对以上问题,本文提出了一种基于载波相频差异矩阵的单通道盲分离算法。

1 单通道同频信号盲分离技术基础

1.1 信号模型

同频信号并不是理论上认为的信号载频完全相同,实际中由于频率发生器不可能完全一致等原因,信号载频无法实现完全一致,所以同频信号是指信号频谱发生了某种程度的混叠,而此时无法通过滤波器来实现信号的区分。本文也是基于这种信号环境来进行单通道盲分离。

设某一信号被载波角频率为w c的余弦信号调制,则调制信号的表达式为:

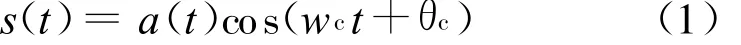
式(1)中,w c为载波角频率,θc为载波初始相位。若接收的混叠信号是多路同频或近似同频的信号,设这些源信号的相位相互独立,则根据式(1)可以得到多路混叠的同频信号的模型为:

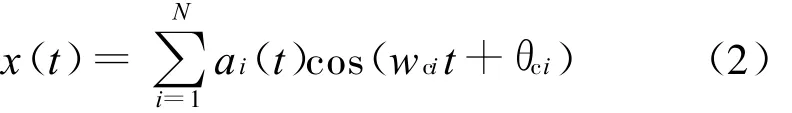
式(2)中,N为源信号个数,ai(t)为第i路信号基带波形,w c i为第i路信号的载波角频率,θc i为第i路信号的载波初始相位。因为该N路信号的载波频率近似,则可用与载波频率近似同频的余弦信号相乘,以第i路信号为例:

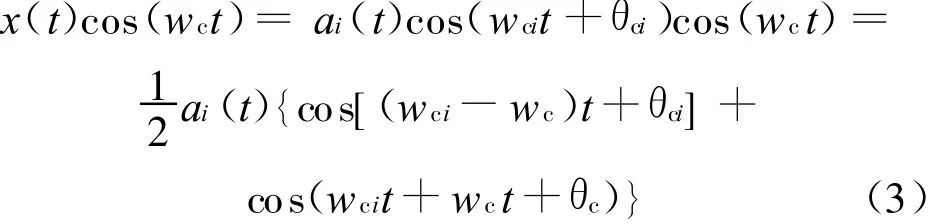
式(3)中,wc为余弦信号载波角频率,滤除高频分量后可得解调信号:

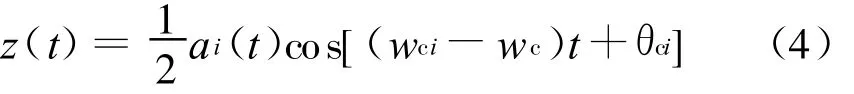
1.2 遗传算法

遗传算法是一种新近发展起来的搜索最优解的方法,它的主要思想是通过模拟生物界自然选择和自然遗传机制,从任意一个初始种群出发,通过选择、交叉和变异操作,产生一群新的具有更高适应度的个体,使群体进化到搜索空间中越来越好的区域。通过这样一代一代地不断进化,最后收敛到一群最适应环境的个体上,即得到问题的最优解。

典型的遗传算法通常用于解决下面这一类的静态最优化问题:

对于n组长度为L的二进制编码bi,i=1,2,…,n,有bi∈ {0,1}L。给定目标函数 f,有 f(bi),并且0＜f(bi)＜+∞,同时满足:f(bi)≠f(bi+1),遗传算法求得满足下式的bi:max{f(bi)|bi∈{0,1}L}。

遗传算法的实施过程包括编码、产生群体、计算适应度、复制、交换、变异等操作。图1详细描述了遗传算法的流程。

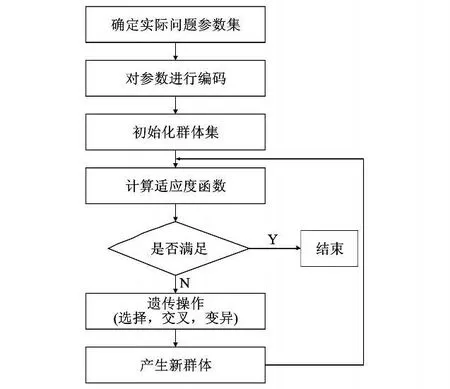
图1 遗传算法流程图Fig.1 The overview framework of genetic algorithm

2 改进的单通道盲分离算法

2.1 基于载波相频差异矩阵的模型

由式(4)可以看出,对于同频混合信号,若不能实现载频的精确估计和相位上的同步,解调后的信号幅度上会出现明显的衰落,对于多相位信号的情况,则还会引起信号不同相位上的衰落差异。而且对于多个同频信号混叠的情况,即使实现其中一路信号的同步也不能滤除其他的混合信号,除非其他的信号在相位上与其正交。

针对以上问题,本文对原始单通道处理模型做出如下改进:

将s(t)按不同的载波相位αj,j=1,2,…,N和载频偏差Δij作N次映射,得到一组不同的新的基带混叠波形:

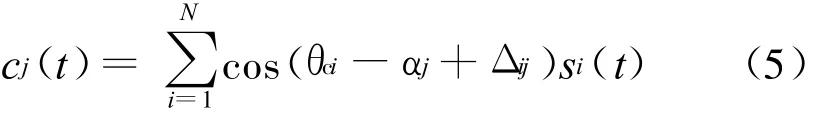
式(5)中,Δij为第i路和第j路信号的载频偏差,cj(t)为在载波相位αj下映射出来的基带混叠信号,则:

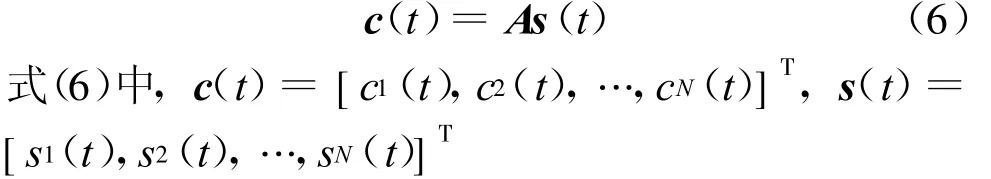
上式中A为构建的载波相频差异矩阵。可以看出,此时已实现了单通道盲分离的多通道处理。

2.2 基于核密度的遗传多通道盲分离算法

传统的基于梯度寻优的遗传盲分离算法,无论是标准梯度还是自然梯度,都无法直接对独立性准则进行优化,因此需要引入非线性函数来代替评价函数。再次,基于梯度来优化解混合矩阵的方法,初始值和步长的设定对寻优的性能影响较大,在解决盲信号分离这样的多峰值寻优问题时,存在着易陷入局部最优解的缺陷。

针对上述算法缺陷,本文结合互信息量最小独立性准则提出了一种基于核密度估计的遗传盲信号分离算法,该算法通过非参数核密度估计,直接估计出输出样本信号的概率分布,并以互信息量为基础给出了遗传算法的适应度函数,通过若干代的遗传进化,得到一个使互信息量最小的分离矩阵,从而实现分离。下面先给出完整的算法流程,然后分别叙述具体步骤。

1)初始化。

2)计算本代种群中每个个体的适应度函数。

3)对本代个体进行选择、杂交、变异操作,并产生出下一代新个体。

4)检查当前进化代数是否大于预定的最大进化代数,若大于,则返回最优个体W*,若不大于,则返回第3)步继续循环。

初始化过程包括采用实数编码方式随机产生ZQ个分离矩阵构成初始种群;设置遗传进化参数,如:初始杂交概率p c0、最大遗传代数Nd等。

在计算每个个体适应度时,本文采用的是互信息最小化作为独立性判据,即下式最小:

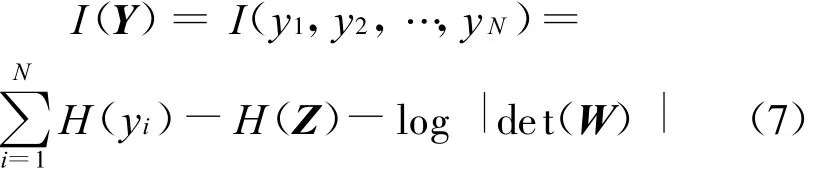
式(7)中,N为源信号个数,Y为估计信号,Z是预处理之后的观测信号,W表示需要寻优的解混矩阵。由于H(Z)是常量,式(7)最小等价于下式最小:

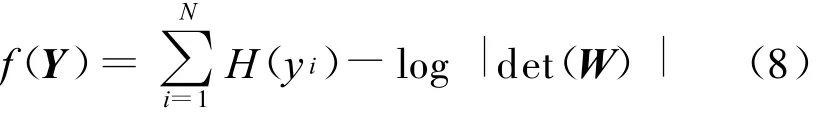
因此,本文选取下式作为适应度函数:

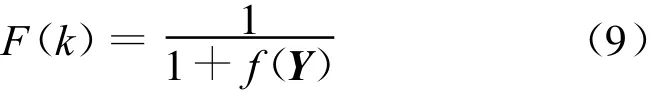
式(9)中,k代表遗传代数。由式(7)—式(9)可以看出,求解适应度函数的关键在于求解估计信号的熵H(y i)。由熵的定义可得:

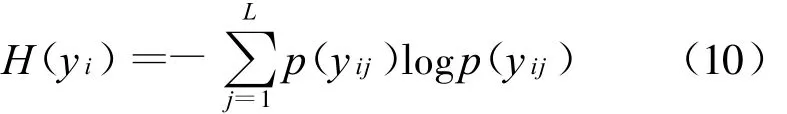
式(10)中,L表示第i路估计信号yi的长度。传统算法中引入非线性函数对信号的概率密度函数及其导数作估计,这种方法具有很大的局限性。本文在此处根据核密度估计法对估计信号的概率直接进行估计:

核函数选取常用的高斯核函数:

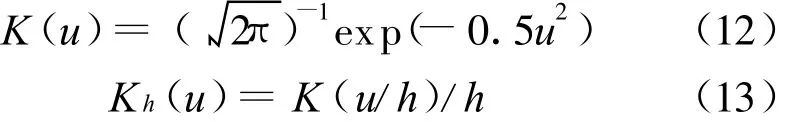
式(12)、式(13)中,K(u)为核函数,h为核带宽,在实际中,h选择经验带宽1.06σ1/5n,σn为样本标准差。

3 算法仿真与分析

3.1 算法设置

以数字调制信号中最为常见的二进制振幅键控信号和二进制相移键控信号为例,基带码元速率都选fm=10 Mb/s,ASK信号载频 fcASK=20.000 1 MHz,载波初始相位θcASK=π/3,BPSK信号载频fcBPSK=20.000 2 MHz,载波初始相位θcBPSK=π/4,基带成型滤波器选取升余弦滤波器,滚降系数a=0.8,系统采样率f s=100 MHz,系统噪声选择加性高斯白噪声。

为了准确评估盲分离系统的性能,我们采用两种性能指标,分别是相似系数ζ和系统矩阵C。源信号和估计信号的相似系数:

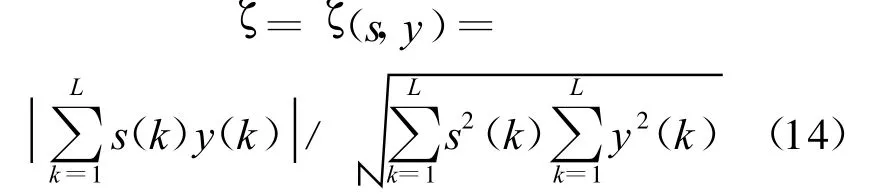
式(14)中,L为信号长度,s(k)为源信号,y(k)为估计信号,若 ζ=1,则认为s(k)与y(k)完全相同,即实现了完全分离。由于估计不可避免地存在误差,所以ζ的值一般接近于1,若ζ的值距离1较远,则认为分离未实现,通常情况下,当ζ的值达到0.9以上,则可认为已达到分离的目的。

系统矩阵是由混合矩阵A和解混矩阵W生成,C=WA。在源信号未知的情况下,采用这种评价准则比较合理。通过比较解混矩阵和实际混合矩阵的乘积C=WA=[Cij]与单位矩阵I之间的差异,就可以评价算法的性能:差异越小,则分离的结果越接近源信号,分离的效果越好。在理想情况下,盲分离算法应能使解混矩阵W收敛于最优W*,使得W*A=I。

3.2 算法分离性能分析

图2给出的是ASK信号和BPSK信号的频谱,由图可知,源信号的频谱在一定范围内发生重叠,稀疏性不强,很难通过常规分离算法来实现分离。

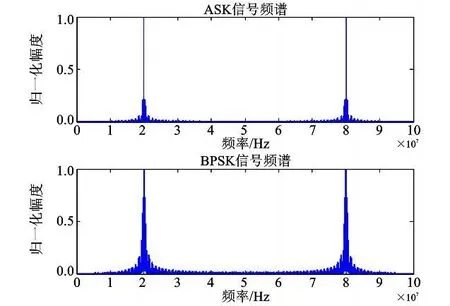
图2 信号频谱比较图Fig.2 Comparison of signal spectrum

图3 给出的是ASK信号和BPSK信号的原始基带波形和经过本文算法分离出的基带波形对比图。在遗传算法中,高斯核函数的带宽选择经验带宽h=1.06,σn为样本标准差。

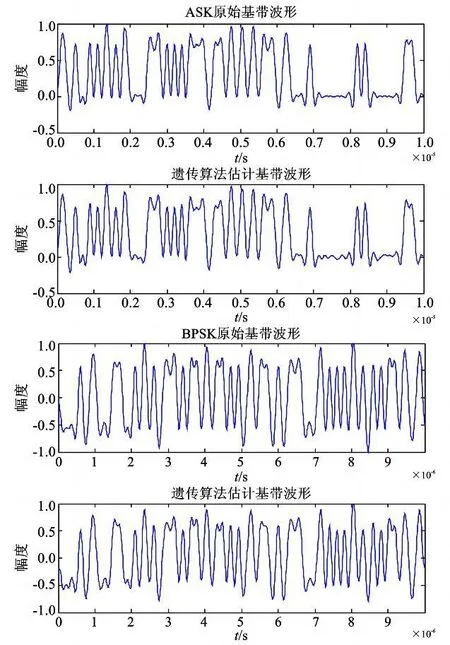
图3 SNR=10 dB情况下遗传算法分离效果图Fig.3 Separation results of genetic algorithm when SNRis set to 10 dB

3.3 算法抗噪性及稳定性分析

为了验证本文算法的抗噪性及稳定性,本文在信噪比0～10 dB的变化范围内,以0.1 dB为步进进行了100次分离实验。图4给出了BPSK信号100次实验得到的相似系数分布图。

由图4可以看出,算法性能会随着信噪比的减小而变差,但波动不明显,并且相似系数的值大多数处于0.9～1的范围内,分离效果理想,由此可看出,本文算法有着较好的抗噪性和稳定性。

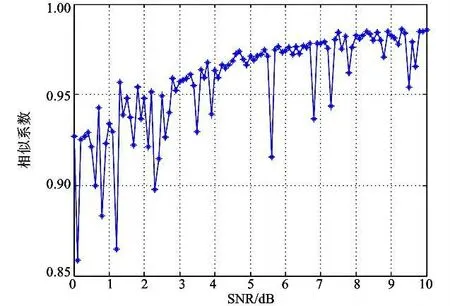
图4 BPSK信号相似系数随信噪比变化曲线Fig.4 Similarity factor of BPSK signal in different value of SNR

4 结论

本文提出了一种基于载波相频差异矩阵的单通道盲分离算法。该算法利用信号分量之间的差异性,通过构建载波相频差异矩阵实现单通道模型到多通道模型的变换。在多通道模型的框架下以基于核密度估计的遗传算法实现了多通道盲分离。仿真实验证明:本文算法能有效解决常规算法适应性较差、分离不完全的问题。

[1]Li Yuanqing,Amari Shun-Ichi,Andrzej Cichocki,et al.Underdetermined Blind Source Separation Based on Sparse Representation[J].IEEE Transactions on Signal Processing,2006,54(2):423-437.

[2]Yilmax,Rickard S.Blind Separation of Speech Mixtures via Time Frequency Masking[J].IEEE Transactions on Signal Processing,2004,52(7):1 830-1 847.

[3]Henry K Kwok,Douglas L Jones.Improved Instantaneous Frequency Estimation Using an Adaptive Short-Time Fourier Transform[J].IEEE Transactions on Signal Processing,2000,48(10):2 964-2 972.

[4]Li Y Q,Cichocki A,Amari S.Analysis of Sparse Representation and Blind Source Separation[J].Neural Computing,2004,16:1 193-1 234.

[5]Cédric Févotte,Simon JGodsill.A Bayesian Approach for Blind Separation of Sparse Sources[J].IEEE Transactions On Audio,Speech,and Language Processing,2006,14(6):2 174-2 188.

[6]James R Hopgood,Peter J W Rayner.Single Channel Nonstationary Stochastic Signal Separation Using Linear Time-Varying Filters[J].IEEE Transaction on Signal Processing,2003,51(7):1 739-1 752.

[7]崔荣涛,李辉,万坚,等.一种基于过采样的单通道 MPSK信号盲分离算法[J].电子与信息学报,2009,31(3):566-568.CUI Rongtao,LI Hui,WAN Jian,et al.An over-sampling based blind separation algorithm of single channel MPSK signals[J].Journal of Electronics&Information Technology,2009,31(3):566-568.