基于广义解调和广义S变换的时频域去噪方法
2011-08-21肖泽龙许建中
柏 晨,肖泽龙,许建中
(南京理工大学电子工程与光电技术学院,江苏南京 210094)
0 引言
利用电磁波对膛内弹丸运动参数测试是目前比较主要的测量方式。然而,在利用该方法进行测试时,由于受到信号选择、反射面确定、电离干扰及外界环境的影响,得到的干涉信号中存在大量的噪声,信号信噪比差。因而,要得到高精度的测试结果,就对后续的数据处理提出了较高的要求[1]。
为了改善信噪比,可以引入小波分解的方法对干涉信号进行预处理以抑制部分噪声,随后利用短时傅里叶变换在时频域对其进行分析[1-2]。而短时傅里叶变换的窗函数固定,对快速变化的信号,其时频分辨率难以得到理想的结果。为了解决这一问题,文献[3]提出利用希尔伯特变换的方法提取信号的相位信息,从相位信息中得到弹丸的运动表达式。但此方法仍是基于信号信噪比较好的情况下得出的。并且与EMD分解相比,小波分解缺乏自适应性,分解后的各个分量仍有可能是多分量信号。文献[4]在对低信噪比信号研究分析的基础上,提出了一种基于希尔伯特黄变换的分析处理方法。但是抑噪效果并不是非常理想,处理后信号的时频脊线图中仍包含有大量奇异点,必然使得计算结果误差增大。
由于传统的时域或频域去噪方法经常受到使用条件的限制,本文提出了基于广义解调和广义S变换的时频去噪方法。
1 理论基础
1.1 广义解调
信号x(t)的广义傅里叶变换(Generalized Fourier Transform,GFT)定义为[5-6]:
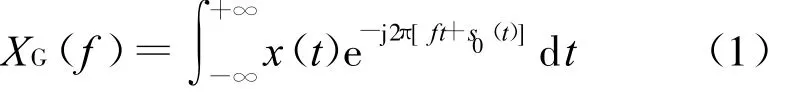
式(1)中,s0(t)是随时间变化的实值函数。实际上是对x(t)e-j2πs0(t)作标准的傅里叶变换。同样,可对XG(f)进行逆GFT变换,得到x(t):
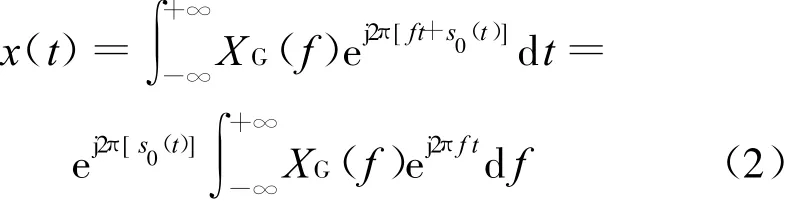
如果 X G(f)=δ(f-f 0),则有 x(t)=ej2π[f0 t+s0(t)],也就是说一个瞬时频率为 f(t)=f0+s′0(t)的信号经过合适的广义傅里叶变换可以将能量集中于频率 f=f0上,其中s′0(t)=d s0(t)/d t。因此只需找到一个近似于s0(t)的相位函数s(t),对信号x(t)进行广义傅里叶变换,得到的解调函数x(t)e-j2πs(t)的时频谱将是一条近似于平行时间坐标轴的,由f=f0确定的直线。这种信号方法称为广义解调[7-8]。
1.2 广义S变换
Stockwell等学者于1996年首次提出了S变换(S-Transform)[9-10]:

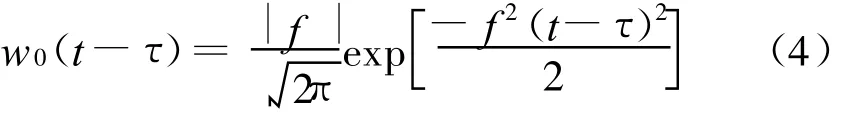
式(4)中,w0(t-τ)为高斯窗口,τ为控制高斯窗口在时间t轴位置的参数,f为频率。并且逆S变换可以表示为:
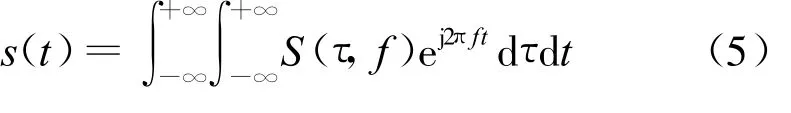
由于S变换中的基本小波形态固定,使得S变换在实际应用中受到一定限制。对S变换的高斯窗进行改造,便得到了广义 S变换(Generalized S-transform)[11]:
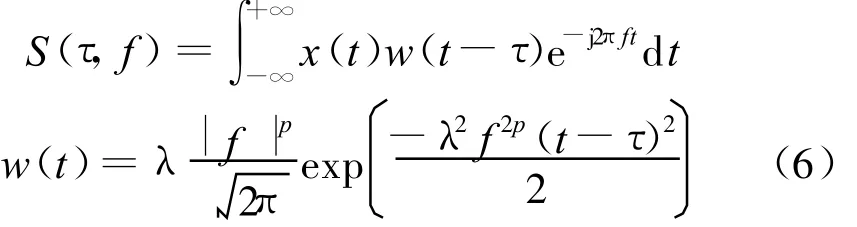
式(6)中,λ、p为调节因子。λ>0,选定 p后,当λ>1时,则时窗宽度随信号频率呈反比变换的速度加快,λ<1则减慢[12],使其具有更好的局部特性。当λ=p=1时,广义S变换即简化为基本的S变换,说明广义S变换与S变换的计算相似,不会增加额外计算量。
2 基于广义解调和广义S变换的信号时频滤波去噪
由前述可知,对于信号 x(t)=A ej2π[f0t+s0(t)],其广义解调信号为 x(t)e-j2πs(t)=A ej2π[f0t+s0t]e-j2πs(t)≈A ej2πf0t,s(t)≈s0(t)为信号 x(t)相位函数的估计值。由式(1)和式(3)共同得到广义解调信号的广义S变换为:
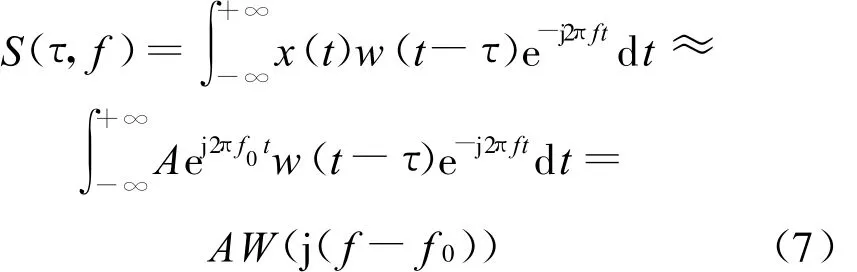
式(7)中,W(j f)为改进的窗函数w(t)的傅里叶变换。式(7)表明,经广义解调后的信号,其广义S变换的时频表示近似为一条平行于时间轴的由f=f0所确定的直线,其分辨率由窗函数本身所决定。
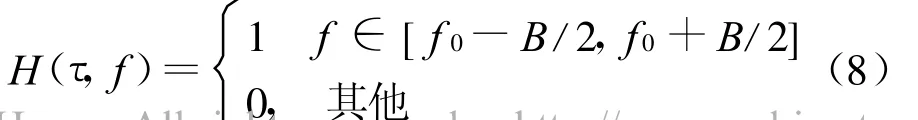
因此,首先对信号进行广义解调和广义S变换,将信号的有用部分在时频域内近似表示为平行于时间轴的一条直线,然后通过时频滤波滤除噪声部分,结合式(7),时频滤波器H(τ,f)的表达式为:式(8)中,f 0是由式(7)所确定的信号时频表示的中心频率,B为由时频分辨率所决定的滤波器的带宽。从式(8)可以看出,滤波器实际上为一平行于时间轴的二维矩形窗“带通”滤波器。考虑到对信号突然截断容易产生边界效应等负面影响,因此对滤波器H(τ,f)进行改进,构造二维梯形窗滤器:

式(9)中,ω1为滤波器衰减起始频率,ω2为截止频率,可以根据信号具体的时频分辨率选取合适的ω1,ω2。由此,可以重构降噪后的信号,结合式(5)和式(9),其重构过程为:
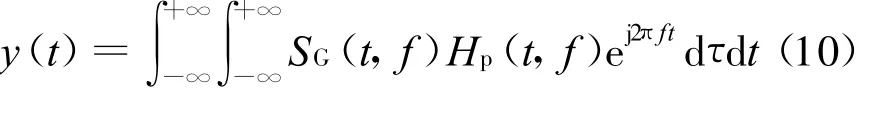
此时,y(t)仍为广义解调信号,需对y(t)进行逆广义解调,即:
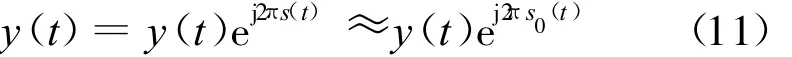
则可得到经降噪后重构的原始信号y(t)。最后由y(t)时频分布提取出相对准确的弹丸运动曲线。
时频域去噪,关键是在时频域设计出高效的二维滤波器。而对于瞬时频率为非线性函数的信号,时频滤波器需要兼顾时间和频率两个方面,往往比较复杂。由式(8)和式(9)可以看出,虽然需要在时频域构造二维滤波器,但是通过广义解调,此滤波器的参数可以完全和时间无关,有效地降低了滤波器的构造难度。并且,与小波变换和短时傅里叶变换相比,逆S变换实际上是广义S变换的时频分布对时间积分后,对其结果进行的傅里叶反变换。它所具有的能量无损特性,使其能够在降噪后的计算过程中对数据精度不产生影响。此外,广义S变换它所具有的高时频分辨率以及其基本小波不必满足容许性条件等独特的优点,使得在克服常规时频滤波缺陷的同时,可以尽可能完整地保留有用信息的时频成分,对即使是信噪比较差的信号,也能得到较为精确的时频曲线。
3 仿真及分析
3.1 试验信号
高精度毫米波干涉运动参数测试系统,通常包括两种微波源:低频微波源和高频微波源。低频微波通常在1~12 GHz频段内,而高频微波通常选在35 GHz,55 GHz和95 GHz频点上,此时火炮身管被视为自由场,弹丸被视为位置可变的反射体。由于采用空间自由场耦合方式,在波束范围内的任何运动都会反映在干涉信号中[1]。因此干涉信号中的高频干扰为噪声的主要部分,所以对这部分噪声的结果直接影响到最终的信噪比和精确度。
在此基础上首先考察一测试信号,并对本文方法的有效性与基于RLS自适应滤波和EMD分解分析的方法进行对比。测试信号为:x(t)=sin(502.66t3-753.98t2+568.48 t+20.13)(加入2 dB高斯白噪声以及20%的高频干扰),信号采样频率为f s=1 000 Hz,采样点数N=1 024,其时域波形如图 1(a)所示 ,时频谱如图1(b)所示。由RLS自适应滤波和EMD分解的方法得到的时频脊线图噪声抑制效果不理想,含有大量奇异点。在此基础上提取的脊线拟合曲线并不十分准确。
采用本文的方法对试验信号进行处理,首先估计信号的相位函数s(t)。从图2(a)可以看到,当t=0 s时,f=85 Hz;t=0.5 s时,f=30 Hz;t=1 s时,f=85 Hz。假设瞬时频率曲线为f(t)=s′(t)=at2+bt+c,根据曲线拟合可以确定相位函数s(t)=80 t2+120 t。这里并没有利用已知信号参数获得参数a、b,而是从图中得到参数的近似值。随后依照前述步骤进行处理。由图2(b)看出信号的主要能量都集中在一条平行于时间轴的直线上,从而可以确定一个只与频率有关的时频域二维“带通”滤波器。经过滤波和重构后的信号广义S变换分布如图2(d)所示,信号的噪声几乎被完全抑制。
为了说明此方法的通用性,在原始模拟信号的基础上,再次加入瑞利分布噪声,其广义S分布如图2(g)所示,去噪效果如2(h)所示。可以看出,对于其他类型的噪声,此方法仍然能够达到预期效果。
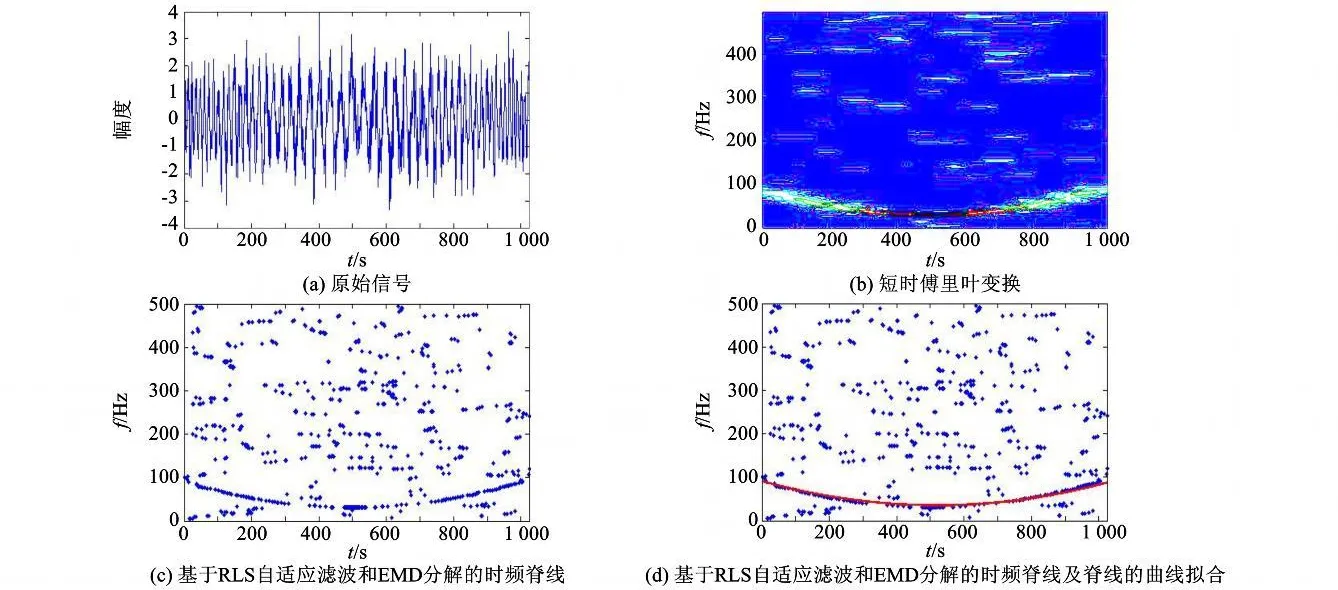
图1 测试信号及基于RLS滤波和EMD分解的处理结果Fig.1 Test signal and the output through the method based on RLS filtering and EMD decomposition
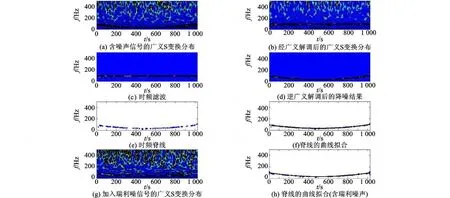
图2 广义解调和广义S变换的去噪结果Fig.2 Denoising output of generalized demodulation and generalized S-transform
图3 对两种方法得出的拟合曲线和理想瞬时频率曲线进行了对比,在相同数量级下,文献[4]方法所得曲线与理想曲线方差的有效数字为8.168 9;而本文方法的方差有效数字为1.785 8。可以看出:采用本文方法,信噪比在明显提高的同时,精确度也得到大幅提高。在此基础上提取的时频脊线和曲线拟合表达准确,拟合程度高。
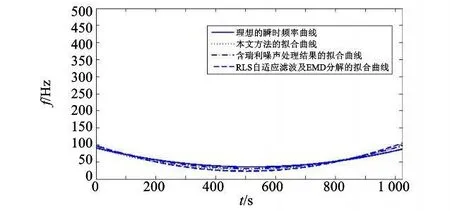
图3 几种拟合曲线和理想瞬时频率曲线对比图Fig.3 Comparison of fitting curves and the ideal instantaneous frequency curve
本文的方法对相位函数的选择并不十分敏感。当相位函数估计不准确时,广义解调后信号的时频分布曲线将不会是平行于时间轴的直线[7,13]。然而,只要误差不超过一定的范围,保证在广义解调后信号的时频分布曲线包含在时频空间的某一个矩形时频带中,由此相应的调节时频滤波器参数,也能达到比较理想的处理结果。
3.2 实际数据分析
为了模拟内膛弹丸运动,采用自行研制的94 GHz干涉仪对某自制土火炮发射过程进行测试,采样频率2 MHz,获得实测数据时域波形图如图4所示(限于篇幅限制,本文已截取有用信号段)。由于信号长度过长,将信号分两组进行运算:第一组对应采样时间0~0.12 s,第二组对应采样时间0.12~0.21 s。如图4所示,可以看出,采用本文所述方法进行处理,显著提高了信噪比,并在此基础上提取出几乎不含奇异点的时频脊线。
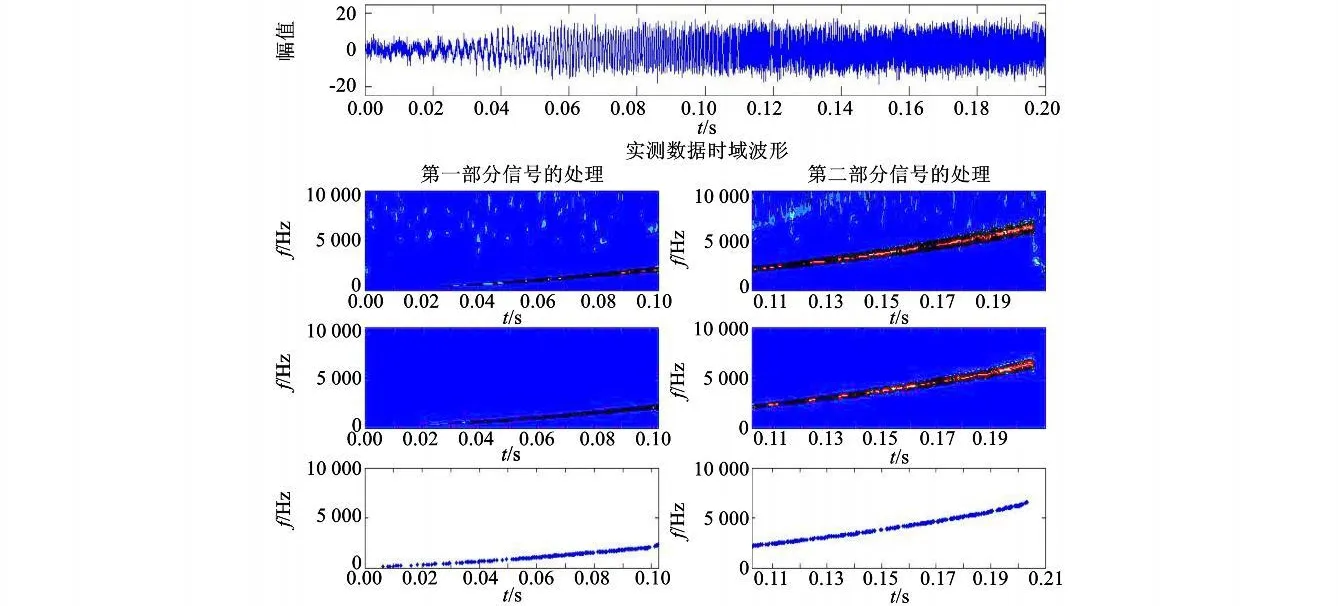
图4 实测数据处理流程Fig.4 Test data processing
将时频脊线进行组合,如图5(a)所示。在此基础上进行二次项曲线拟合,并根据多普勒频率公式推导出弹丸在堂内运动的速度曲线及加速度曲线。由图5(c)可知,弹丸出膛后速度在0.205 s左右达到最大,为28.16 m/s。相应弹丸运动距离,即反射板到炮口距离以及炮筒长度共2.310 2 m。与实际相符,验证了结果的准确性。
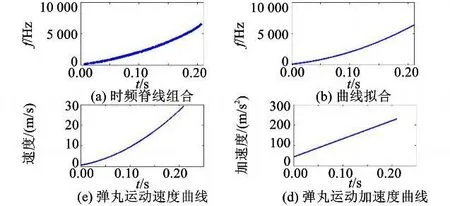
图5 弹丸运动曲线Fig.5 Curves of bullet motion
4 结论
本文提出一种基于广义解调和广义S变换的方法,使得广义S变换的时频分布为近似平行于时间轴的一条直线;然后在时频域构造与时间因子无关的二维时频带通滤波器去除噪声,降低了滤波器的构造难度;最后重构信号并由此提取弹丸运动曲线。仿真结果表明:与 RLS自适应滤波和希尔伯特黄(HHT)变换相比,本文方法显著提高了信号的信噪比,增加了所得结果的准确度。此外,广义S正反变换具有的能量无损特性,与奇异值分解(SVD)等降噪方法相比,不需要假设噪声与信号的相关性差,并且计算量少,运算速度快。本文提出的方法能够准确地表述弹丸运动模型,是一种有效的处理方法。但是,如何有效地选取相位函数以及设计更高效的时频滤波器,还需要进一步的研究和完善。
[1]王黎明,赵英亮,韩焱.高速运动目标测试数据处理精度的方法研究[J].华北工学院学报,2005,26(1):53-57.WANG Liming,ZHAO Yingliang,HAN Yan.The methods of increasing the data processing precision of highspeed moving object[J].Journal of North China Institute of Technologe,2005,26(1):53-57.
[2]王黎明,赵昕,刘洪涛,等.微波干涉仪测试数据处理方法[J].火炮发射与控制学报,2004(4):63-66.WANG Liming,ZHAO Xin,LIU Hongtao,et al.Method of test data processing on microwave interferometer[J].Gun Launch&Control Journal,2004(4):63-66.
[3]肖剑,柳斌,郭亚龙,等.基于希尔伯特变换的干涉仪信号处理[J].探测与控制学报,2010,32(1):80-83.XIAO Jian,LIU Bin,GUO Yalong,et al.Signal processing of microwave interferometer based on hilbert transform[J].Journal of Detection&Control,2010,32(1):80-83.
[4]陶金泉.毫米波干涉仪信号处理研究[D].南京:南京理工大学电光学院,2009.
[5]Olhede S,Walden A T.A generalized demodulation approach to time-f requency projections formulticom-ponent signals[J].Proceeding s of the Royal Society A,2005,461(2059):2 159-2 179.
[6]Zhi Pengfang,Fulei Chu,Ming J Zuo.Time-frequency analysis of time-varying modulated signals based on improved energy separation by iterative generalized[J].Journal of Sound and Vibration,2011,33(6):1 225-1 243.
[7]杨宇,程军圣,于德介.广义解调时频分析方法中的若干问题探讨[J].振动与冲击,2008,27(2):19-24.YANG Yu,CHENG Junsheng,YU Dejie.Study on some problems in the generalized demodulation time-f requency analysis method[J].Jouranl of Vibration and Shock,2008,27(2):19-24.
[8]罗向龙,高静怀.基于广义解调和奇异值分解的时频表示增强[J].数据采集与处理,2010,25(4):419-424.LUO Xianglong,GAO Jinghuai.Enhancing time-frequency representation based on generalized demodulation and SVD[J].Journal of Data Acquisition&Processing,2010,25(4):419-424.
[9]Stockwell R G,et al.Localization of the complex spectrum:The S-transform[J].IEEE Transactions on Signal Processing,1996,44(4):998-1 001.
[10]Stockwell RG.A basis for efficient representation of the S-transform[J].Digital Signal Processing,2007,17(1):371-393.
[11]高静怀,陈文超,李幼铭,等.广义S变换与薄互层地震响应分析[J].地球物理学报,2003,46(4):526-532.GAO Jinghuai,CHEN Wenchao,LI Youming,et al.Generalized S transform and seismic responseanalysis of thin interbeds[J].Chinese Journal of Geophysics,2003,46(4):526-532.
[12]赵淑红,朱光明.S变换时频滤波去噪方法[J].石油地球物理勘探,2007,42(4):402-408.ZHAO Shuhong,ZHU Guangming.Time-frequency filtering to denoise by S transform[J].OGP,2007,42(4):402-408.
[13]Junsheng Cheng,Yu Yang,Dejie Yu.The envelope order spectrum based on generalized demodulation time-frequency analysis and its application to gear fault diagnosis[J].Mechanical Systems and Signal Processing,2010,24(2):508-521.
