基于引信头锥摆动的火箭弹弹道修正方法

王梦龙,王 华,韩 晶

(北京航空航天大学宇航学院,北京 100191)

0 引言

现代战争对武器系统的打击精度提出了新的要求,赋予引信弹道修正能力,可以提高大量库存常规弹药的射击精度。实现二维弹道修正采用的修正执行机构主要有两种,一类是微型脉冲发动机或射流喷管,该装置具有体积小、重量轻、无活动部件、无伺服机构、响应时间短等特点,现已成功应用于精确制导弹药上,但其结构复杂,无法实现连续修正,而且受空间尺寸的限制很难在引信上使用[1-2];另一类是利用鸭式空气舵连续生成弹道修正所需的法向及侧向分力,目前这种方法在修正弹上已经得到运用,但在二维弹道修正引信方面的应用还不成熟。

相关研究人员对头部偏摆的火箭弹进行了气动分析及初步的弹道仿真,讨论了弹丸头部有控弯曲摆动式弹道修正方法[3-4]。对偏头控与舵翼两种控制方式的气动特性作了比较深入的研究,结果表明:舵翼性能随飞行马赫数上升而急剧下降,在超音速域,相对于舵翼控制,偏头控制更有效[5],且鸭舵自身重量较轻,产生的惯性力远小于升力,无法有效平衡铰链力矩[6]。此方法采用压电陶瓷堆作为驱动源,经过机械放大后可输出4.5°的角位移。火箭弹头部偏摆具有结构简单、气动热环境相对良好、气动控制简单独特、弹道修正时的配平升力可调等优点,但涉及到全弹的结构变动。

上述方法均不适用于当前库存火箭弹大批量升级改造,本文针对提高现有库存弹药打击精度问题提出了基于火箭弹引信头锥摆动的弹道修正方法。

1 研究对象

微旋火箭弹转速低,便于引信头锥在一个旋转周期内换向控制的实现,故本文以一种火箭弹的二维弹道修正为背景进行研究。

火箭弹尾翼为直翼,无尾缩,总长度为 2 925 mm,弹头部分长452 mm,为尖锥形。在飞行过程中,转速维持在11～25 r/s范围内,弹道降弧段,弹丸转速在10～15 r/s之间,速度维持在300～400 m/s之间。射击的距离和方向误差按32 km射程上火箭弹最大射击误差战术指标——距离1/150、方向1/75计算得出分别为213.33 m、426.67 m。其电子时间引信长195.59 mm,约占整个弹长的6.6%,外露部分长160 mm。

2 火箭弹引信头锥偏摆弹道修正方法

头锥摆动式弹道修正引信通过驱动装置来改变引信头锥的摆动角度和摆动方向,产生相对弹体的附加气动力和气动力矩,达到修正弹药落点位置的目的。火箭弹引信头锥偏摆弹道修正是通过二维弹道修正引信的修正执行装置——引信头锥摆动式弹道修正机构实现的。在本执行机构设计方案中,动力源采用的是永磁直流电机,主要利用电机的输出转矩和转速。设计的执行机构结构如图1所示。

传动机构采用的是齿轮与蜗轮蜗杆的组合,蜗轮蜗杆机构一方面把旋转运动转换为摆动运动,另一方面蜗轮蜗杆的自锁能力又满足了头锥所需要的锁定功能,引信外露160 mm可以满足执行机构对空间的要求。火箭弹转速为15 r/s时,机构延迟时间最大为16.66 ms,要求电机提供的最大转矩为180 mN◦m。火箭弹转速为7 r/s时,机构延迟时间最大为35.7 ms,要求电机最大转矩为98 mN◦m。考虑到符合尺寸要求微型电机所能提供的转矩最大为110 mN◦m,则必须减旋,使其转速维持在7 r/s以内,修正执行机构才能完成有效修正。

3 气动仿真分析

火箭弹气动力参数对弹道修正能力有着决定性影响,因此,气动力参数的精确计算是研究火箭弹引信头锥摆动弹道修正方法的重要一环。

3.1 火箭弹引信头锥偏摆气动仿真模型

引信头锥摆动产生的控制力在头部,虽然此力较小,但它离全弹质心较远,力臂长,因而控制力矩大,控制效率高,通过小角度的引信头锥偏转,可产生较大的机动过载。

图2为火箭弹上引信头锥摆动产生对弹体修正力及力矩的原理示意图,图中α为高低攻角,αb为引信头锥摆角,Rx、Ry、Mz为由火箭弹攻角引起的气动阻力、升力、俯仰力矩,M h为俯仰阻尼力矩,Rx b、Ryb、Mzb为由引信头锥摆角引起的附加气动阻力、升力、俯仰力矩。

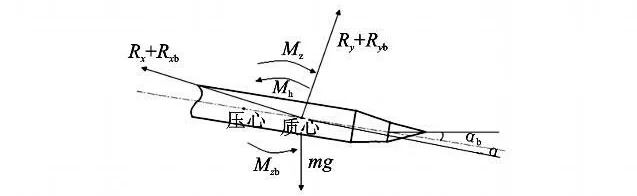
图2 引信头锥摆动时火箭弹受力图Fig.2 Force diagram of rocket when nose cone of fuzeis swinging

为了能够更加真实地模拟流场,避免流场区域过小而出现壁面干扰现象,选定弹体表面距计算区域边界的距离为10倍弹长,约为30 m,由于计算模型具有面对称性、流场对称、初始条件及边界条件对称,为提高计算精度,减少计算时间,只需建立关于对称面对称的一半模型进行仿真,即计算区域为一半径30.2 m,高63.2 m的半圆柱。为了提高仿真精度和速度,同时满足湍流仿真和粘性仿真的要求,对弹体周围的网格做加密和附面层控制(如图3所示),外部由较稀疏的结构化网格构成(如图4所示)。仿真模型区域如图5所示。

图3 对称面网格划分Fig.3 The division of grid on the symmetry plane

图4 体网格划分Fig.4 The division of grid

图5 计算模型区域Fig.5 The region of calculation model

3.2 气动仿真结果及分析

应用流体计算软件FLUENT仿真了入口流速在1.3 Ma、1.5 Ma 、2.0 Ma 、2.5 Ma 时引信头锥偏角分别为 0°、3°、5°、8°、12°、15°时的升力、阻力和力矩。

火箭弹引信头锥部分和弹体中轴线有一个可控的相对偏角(0°～15°)。此偏角导致引信头锥上下区域流场不对称,弹头下表面区域的压强明显高于上表面区域的压强(图6显示了头锥摆角为8°时,对称面上的压力分布),压差的存在使得火箭弹头部产生一个附加升力,同时也造成压心前移,产生附加的俯仰力矩,使得火箭弹从原有的平衡姿态调整到新的平衡姿态[2]。因此,可以通过精确控制头锥摆角,产生附加气动力来有效实现二维弹道修正功能。

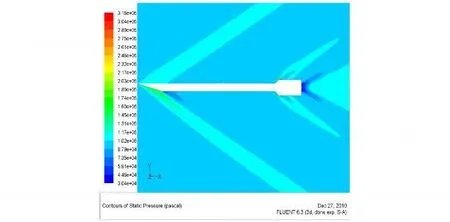
图6 摆角8°时对称面压强分布Fig.6 Pressure distribution on symmetry plane when swing angle of nose cone is 8°

表1 某火箭弹阻力系数计算值与实验值对比(0°攻角)Tab.1 The drag coefficient Comparison of simulation to wind tunnel test(angle of attack 0°)

阻力系数仿真一直是数值仿真中的难题,尤其是对较复杂的流动,网格的划分、初始条件及边界条件的设置、湍流模型的选取等都会对其计算精度产生影响[7]。表1为阻力系数仿真结果,将其与该火箭弹相同条件下的风洞试验阻力系数值比较,其最大误差为19%,表明其仿真结果合理可信。可以预测,升力系数与俯仰力矩系数应有较高仿真精度。

由表1数据可知,相同马赫数下,全弹阻力系数随着头锥摆角的增加略有增加,虽然阻力系数随着马赫数的增加而减小,但是全弹阻力随着马赫数的增加而增大,全弹阻力系数变化曲线如图7所示。

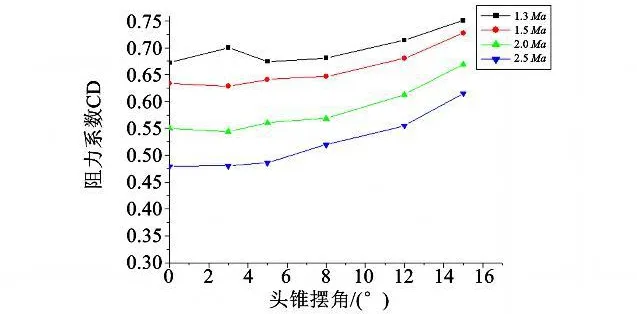
图7 阻力系数随引信头锥摆角变化曲线Fig.7 The relation curves between drag coefficient and swing angle of nose cone

作用在火箭弹上的升力主要是由弹翼、弹体以及弹翼与弹体之间的相互干扰产生。全弹升力随引信头锥摆角变化曲线如图8所示。

图8 升力系数随引信头锥摆角变化曲线Fig.8 The relation curves between lift coefficient and swing angle of nose cone

俯仰力矩的大小与压心的位置密切相关,造成压心位置改变的主要原因就是头锥摆角产生一个附加的气动力,全弹俯仰力矩变化曲线如图9所示。

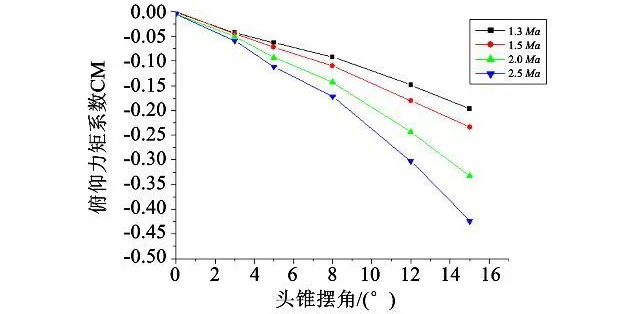
图9 俯仰力矩系数随引信头锥摆角变化曲线Fig.9 The relation curves between pitching moment coefficient and swing angle of nose cone

由图6—图8可看出:全弹攻角0°时,在同一马赫数情况下,改变引信头锥摆角,阻力系数变化较小,而升力和俯仰力矩系数变化明显,气动性能改变显著。速度越大,随着头锥摆角变化,升力系数曲线斜率越大,升力增加幅度越大,其控制效率越高。

通过数据比较得知,该火箭弹引信头锥气动效能随着速度的增加而提高。速度较低时,头锥摆角产生的气动升力和俯仰力矩都很有限;速度较大时,头锥摆角产生的气动升力和俯仰力矩较大,较小的头锥摆角就可以产生较大的气动控制力。

4 弹道及修正能力仿真分析

基于经典力学和空气动力学理论,分析了火箭弹的受力情况和空间运动过程,不考虑弹丸自转,运用经典的六自由度火箭弹运动方程组[8],建立了火箭弹的空间六自由度弹道模型,编制了Matlab仿真程序,利用之前的气动力仿真值对基于引信头锥摆动的火箭弹修正外弹道进行了数值仿真分析。

4.1 弹道特性

典型外弹道仿真结果表明,火箭弹的弹道较高,速度在火箭发动机推力的作用下由初始出炮口的51.69 m/s在短时间内迅速增大到1 000 m/s以上,在弹道顶点时最低约为292 m/s,降弧段速度维持在300～400 m/s之间。火箭弹落地速度约为350 m/s。火箭弹总共飞行115 s,在发射后50 s达到弹道顶点。火箭弹飞离发射架时由于初始扰动的影响弹体有较小波动,高低攻角曲线是振幅迅速衰减的正弦曲线(如图10所示),发射后3 s达到稳定状态,振幅衰减的原因主要是由于稳定力矩的作用。

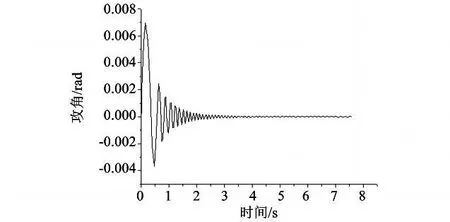
图10 无控弹道下火箭弹高低攻角历程曲线Fig.10 History curve of angle of attack without trajectory correction

引信头锥有摆角时,弹体高低攻角除了在初始出现由起始扰动引起的较小波动外,在起控点及后续弹道段也出现较小的波动,这是由头部攻角的突变引起的。由于降弧段速度较低,因此弹体波动持续时间更长[3]。图11为火箭弹发射后50 s起控的高低攻角变化曲线。

图11 弹道修正时火箭弹高低攻角历程曲线Fig.11 History curve of angle of attack with trajectory correction

4.2 引信头锥摆角、起控时间与修正量的关系

为找到引信头锥摆角、起控时间与修正量的关系,仿真分析了几组不同引信头锥摆角、起控时间下的射程修正量和侧向修正量的关系,表2、表3给出了以 53°角发射时引信头锥摆角为 3°、5°、8°、12°、15°,起控时间分别为 20 s、50 s、70 s和 90 s时的射程修正量和侧向修正量。从表2和表3中数据可以看出,射程修正量最大可达3 070 m,侧向最大修正量可达1 690 m,且都与引信头锥摆角近似成线性关系。表2、表3中的数据都是由最大周期平均操纵力得来的,且假设引信头锥偏转机构的响应时间为0,所以实际修正量会比表中的修正量小。起控时间对射程修正量影响也很大,早起控的修正量大,因此需综合考虑选取修正方式。

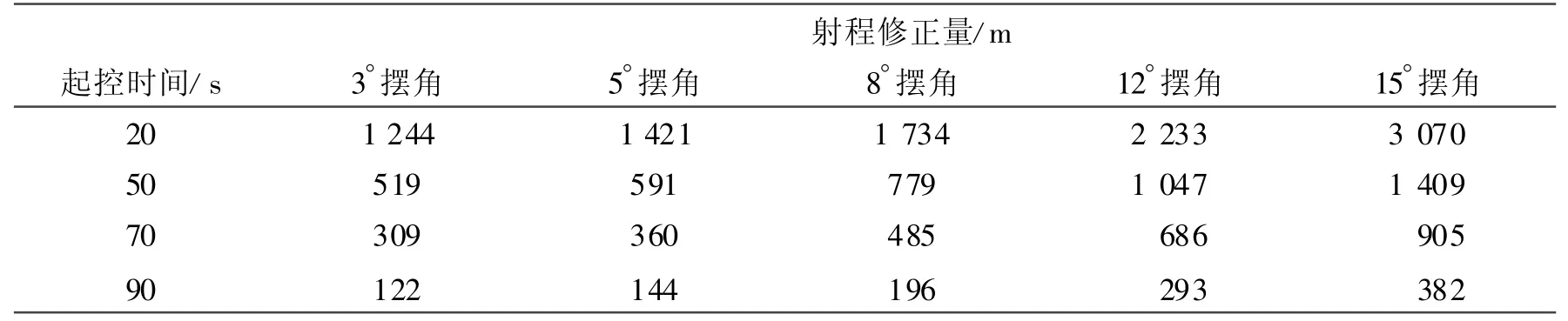
表2 不同引信头锥摆角和起控时间下的射程修正量Tab.2 The correction value of range with different swing angleof nose cone and initial control time

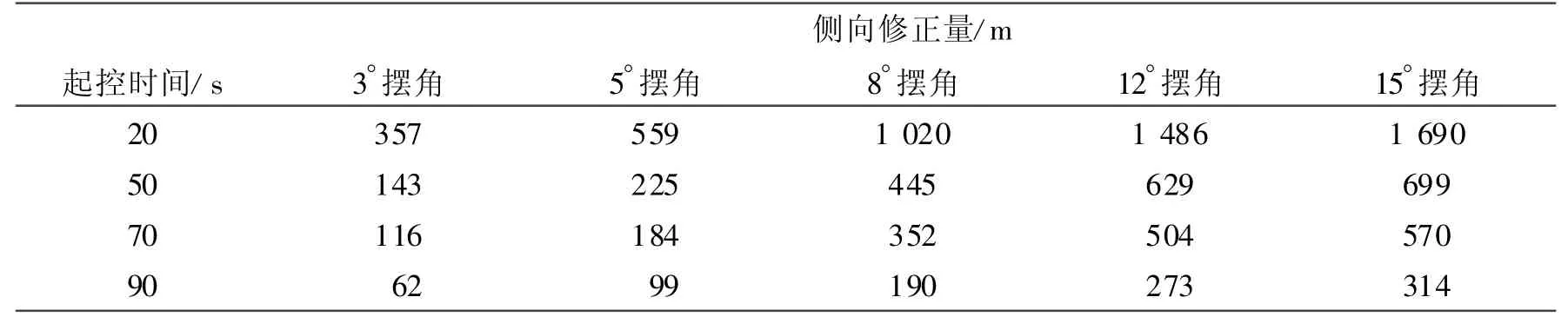
表3 不同引信头锥摆角和起控时间下的侧向修正量Tab.3 The correction value of side with different swing angle of nose cone and initial control time

5 结论

本文提出了基于火箭弹引信头锥摆动的弹道修正方法。该方法通过电机驱动控制引信头锥摆角改变全弹气动外形,产生二维弹道修正所需附加修正力及力矩,达到修正弹道落点的目的。仿真试验结果表明:火箭弹高速飞行时,引信头锥偏摆可以产生良好的气动控制特性;飞行速度较低时,产生的气动控制力虽然比较小,但是考虑到其对火箭弹整个飞行轨迹的影响,还是比较可观的。由表2、表3可知:原则上,头锥摆动式弹道修正引信的修正能力可以基本满足二维弹道修正的要求,但修正执行机构适应转速范围较窄,提高修正执行机构的适应转速是后续研究的主要方向。

[1]朱锐,董二宝,张杰,等.头部可偏转飞行器气动仿真与外形优化[J].机械与电子,2008(8):6-8.ZHU Rui,DONG Erbao,ZHANG Jie,et al.Simulation and optimization of aerodynamic characteristics of aerocraft with a deflected angle of forehead[J].M achinery&Electronics,2008(8):6-8.

[2]李明,陈智刚,董素荣,等.亚音速条件下可偏转头部弹气动特性研究[J].弹箭与制导学报,2010,30(5):147-148.LI Ming,CHEN Zhigang,DONG Surong,et al.Aerodynamic characteristics of missile with a deflected angle of forehead in subsonic flow[J].Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(5):147-148.

[3]魏方海,王志军,尹建平.有头部偏角的尾翼火箭弹气动性能数值计算[J].弹箭与制导学报,2006,26(S3):553-558.WEI Fanghai,WANG Zhijun,YIN Jianping.Numerical calculation of aerodynamic characteristics of shell with an angle of warhead[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(S3):553-558.

[4]魏方海,王志军,吴国东.控制火箭弹头部偏角的弹道修正技术[J].弹箭与制导学报,2006,26(2):928-930.WEI Fanghai,WANG Zhijun,WU Guodong.A new method of ballistic correction by controlling the nose angle of rocket[J].Journal of Projectiles,Rockets,Missiles and Guidance,2006,26(2):928-930.

[5]高欣欣.偏头控气动特性研究[C]//中国航空学会2006航空飞行器发展与空气动力学研讨会论文集.杭州:中国航空学会空气动力学专业委员会,2006:95-99.

[6]William J.Larkin,Mitchell Thomas.Atmospheric Flignt of a Variable-Bend Body[J].Jounal of Guidance and control,1979,2(5):382-387.

[7]刘洋,韩晶.头锥摆动式二维弹道修正引信的气动特性分析[C]//中国兵工学会第十六届引信学术年会论文集.西安:中国兵工学会引信专业委员会,2009:372-375.

[8]钱杏方,林瑞熊,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000.